机器学习笔记：局部加权回归 LOESS

Posted 2022-02-18 UQI-LIUWJ

0 前言

        对于预测问题，回归中最简单的线性回归，是以线性的方法拟合出数据的趋势。

        但是对于有周期性，波动性的数据，并不能简单以线性的方式拟合，否则模型会偏差较大

        局部加权回归（lowess）能较好的处理这种问题。可以拟合出一条符合整体趋势的线，进而做预测。‘

        同时，局部加权回归（lowess）也能较好的解决平滑问题。

        在做数据平滑的时候，会有遇到有趋势或者季节性的数据，对于这样的数据，我们不能简单地将均值正负3倍标准差以外的点视为异常值剔除，需要考虑到趋势性等条件。

        使用局部加权回归，可以拟合一条趋势线，将该线作为基线，偏离基线距离较远的则是真正的异常值点。

1 基本思想

        以一个点x为中心，向前&后截取一段长度为frac的数据，对于该段数据用权值函数w做一个加权线性回归

        记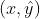为该回归线的中心值，其中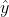为拟合后曲线对应值。

        对于所有的n个数据点则可以分别做出一条加权回归线，每条回归线的中心值的连线则为这段数据的Lowess曲线。
 

        在局部加权回归中，可以调整的参数有：

步长 frac	应该截取多长的数据，来进行局部回归
权值函数w	这个后面会详细说
迭代次数it	进行几次局部加权回归迭代
回归间隔delta	不一定每个数据点都需要拟合一条加权回归先，可以间隔几个算一次，中间的点用某种插值计算即可

2 权值函数

2.1 权值函数需要满足的条件

（1）

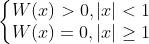
（2）W(x)=W(-x)

（3）当x≥0的时候，W(x)非增 

【换句话说，希望权值函数最中间（0）的值较大，两侧的值较小】

2.2 常见的权值函数

2.2.1 B函数 （二次函数）

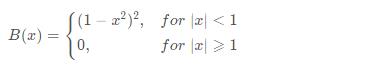
2.2.2 W函数（三次函数）

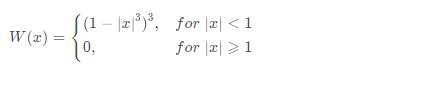
 2.2.3 二次函数和三次函数的取舍

二次与三次函数的区别在于，三次函数对于周围权值降速更快，在平滑最初时候效果好

因此对于权值函数选取，第一次迭代适用W函数（三次函数），之后迭代使用B函数（二次函数）。

2.3 权值函数的使用方法

1 将数据段[x-frac/2,x+frac/2] 映射到[-1,1]

2 带入使用的权值函数W(x)，计算出每个点的wi

3 使用加权回归得到x点附近的局部加权回归曲线：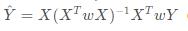

 机器学习笔记：线性回归_UQI-LIUWJ的博客-CSDN博客

3 回归迭代

我们记：ground truth为y，预测值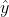为,残差为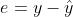，e的中位数为s

于是我们有：权值调整附加值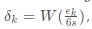，其中修正后的权值为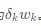

3.1 迭代过程

1 使用W函数作为第一轮的权值函数，求出w

2 将w带入加权回归，求出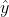

3 计算e和s

4 以B函数作为之后轮次的修正权值函数，求出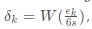

5 计算 修正后的权值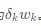

6 以修正之后的权值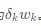作为新的w，重复2，3，4，5的迭代过程