opencv-python图像处理 ---直方图与傅里叶变换逆变换

Posted 2022-02-05 NewSuNess

一、直方图
代码里的cv-show函数：

def cv_show(img):
    cv.imshow("hh", img)
    cv.waitKey(0)
    cv.destroyAllWindows()

从统计的角度讲，直方图是图像内灰度值的统计特性与图像灰度图之间的函数，直方图统计图像内各个灰度级出现的次数。从直方图的图形上观察，横坐标是图像中各像素点的灰度级，纵坐标是具有该灰度级的像素个数。
cv2中的函数使用：

hist = cv2.calcHist([src], channels, mask, histSize, ranges, accumulate)

src:对应输入图像，其图像格式为uint8或者float32,需要用[]括起来传入
channels: 指定通道编号，也需要[]，如果是灰度图，channels=[0], 如果是彩色图像，channels=[0]、[1]、[2]，分别对应B, G, R
mask:掩模图像。当统计整幅图像的直方图时，将这个值设为None， 统计某一部分时，需要用到掩模图像。
histSize：BINS的值，使用需要[]括起来，BINS的意思是：参数子集的数目，在处理数据过程中，有时需要将众多的数据划分为若干组，再进行分析。
ranges:像素值的范围，八位像素值就是[0~255]
accumulate:布尔型累计标记。如果不为假，则直方图再开始计算时不会清零，而是在上一次运行的基础上继续进行统计。
代码：

def calc_hist():
    img = cv.imread("car_red.jpg", cv.IMREAD_GRAYSCALE)
    dis = cv.calcHist([img], [0], histSize=[256], ranges=[0, 255], mask=None)
    plt.hist(img.ravel(), 256)
    plt.show()

掩码操作：使用掩码可以获得图像的某一部分图像：

def calc_hist():
    img = cv.imread("car_red.jpg", cv.IMREAD_GRAYSCALE)
    # 创建掩模
    mask = np.zeros(img.shape, np.uint8)
    mask[50:250, 50:400] = 255
    cv_show(mask)
    # 将原图像与mask执行与操作，就能得到mask位置的图像
    mask_img = cv.bitwise_and(img, mask)
    cv_show(mask_img)

使用直方图展示掩码前后两张图片的直方图统计：

def calc_hist():
    img = cv.imread("car_red.jpg", cv.IMREAD_GRAYSCALE)
    # 创建掩模
    mask = np.zeros(img.shape, np.uint8)
    mask[50:250, 50:400] = 255
    cv_show(mask)
    # 将原图像与mask执行与操作，就能得到mask位置的图像
    mask_img = cv.bitwise_and(img, mask)
    cv_show(mask_img)
    dis = cv.calcHist([img], [0], histSize=[256], ranges=[0, 255], mask=None)
    dis_mask = cv.calcHist([mask_img], [0], histSize=[256], ranges=[0, 255], mask=None)
    plt.plot(dis)
    plt.plot(dis_mask)
    plt.show()

执行结果：

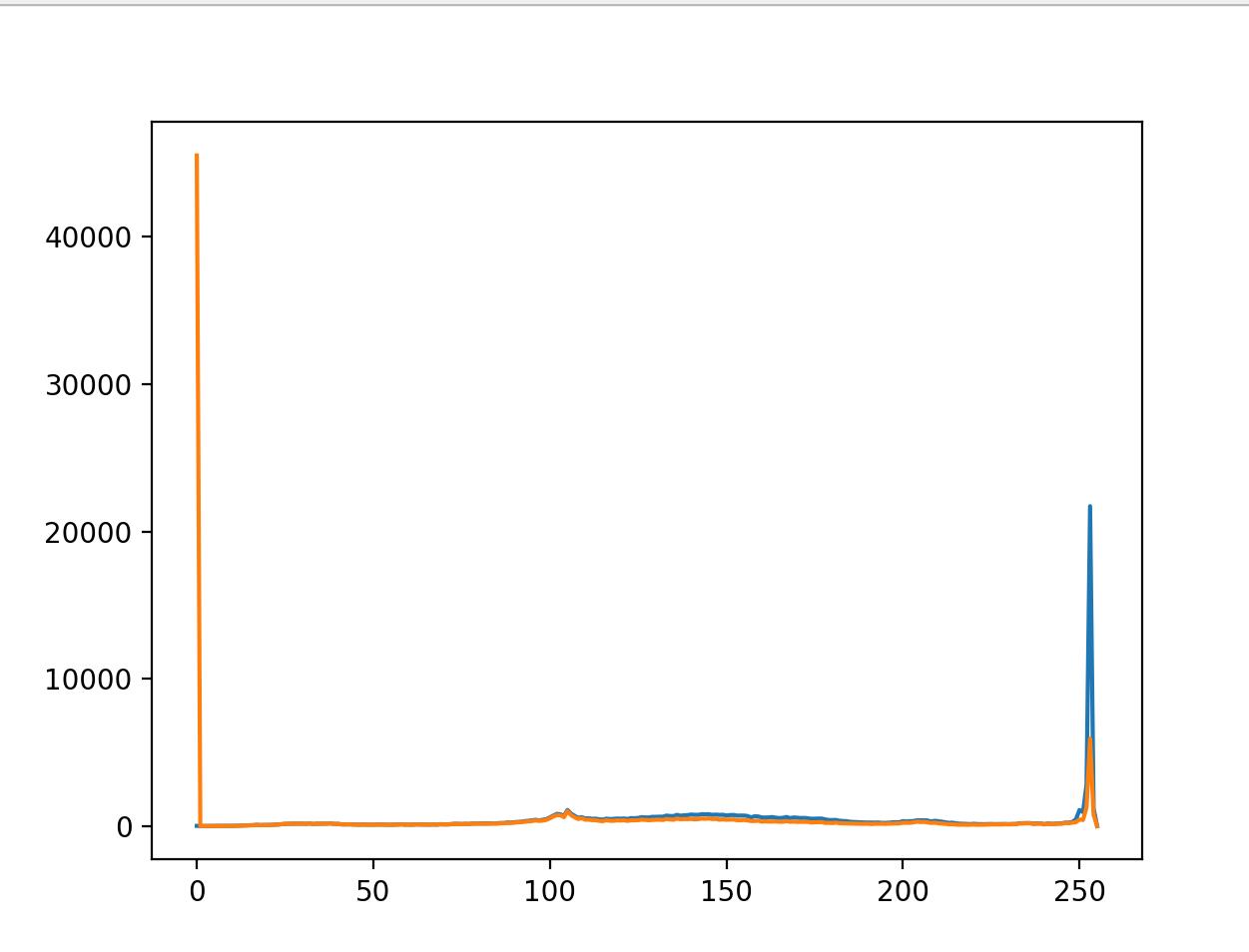
直方图均衡化：由于统计得到的直方图，有些像素点的数量很多，有的非常少，例如上图。方法就是计算累积概率，然后根据累积概率重新映射灰度值，再将结果取整数。

def calc_hist():
    img = cv.imread("cup.jpg", cv.IMREAD_GRAYSCALE)
    # 创建掩模
    mask = np.zeros(img.shape, np.uint8)
    mask[50:250, 50:400] = 255
    cv_show(mask)
    # 将原图像与mask执行与操作，就能得到mask位置的图像
    mask_img = cv.bitwise_and(img, mask)
    cv_show(mask_img)
    dis = cv.calcHist([img], [0], histSize=[256], ranges=[0, 255], mask=None)
    dis_mask = cv.calcHist([mask_img], [0], histSize=[256], ranges=[0, 255], mask=None)
    # 均衡化
    equ = cv.equalizeHist(img)cup
    plt.hist(equ.ravel(), 256)
    plt.plot(dis)
    plt.show()
    # 均衡化后的图像
    cv_show(equ)

效果图：

由于我使用的图片本身像素点分化就特别严重，因此使用均衡化之后效果还是不够好。均衡化后，由于改变了像素点，其图片内容也会改变。在某些情况下，该操作会使图片丢失一些特征。

二、傅里叶变换在图像中的应用
图像处理一般分为空间域处理与频率域处理。空间域处理主要划分为灰度变换和空间滤波两种形式。
频率域处理是先将图像变换到频率域，然后再频率域对图像进行处理，最后再通过反变换将图像从频域变换到空间域。在图像处理过程中，傅里叶变换就是将图像分解为正弦分量和余弦分量两部分。数字图像经过傅里叶变换后，得到的频域值是复数。因此，显示傅里叶变换的结果需要使用实数图像和虚数图像或者幅度图像加相位图像的形式。
对图像进行傅里叶变换后，能够得到图像中的低频信息和高频信息。低频信息对应图中变换缓慢的灰度分量，高频信息对应图中变化很快的灰度分量，是由灰度的尖锐过渡造成的。
1、使用numpy实现傅里叶变换：

result = numpy.fft.fft2(img)

传入参数需要是灰度图像，函数的返回值为一个复数数组。

def fft():
    img = cv.imread("cup.jpg", cv.IMREAD_GRAYSCALE)
    # 傅里叶变换 ，0频率在左上角
    result = np.fft.fft2(img)
    # 将位于左上角的0频率移到图像中间
    result = np.fft.fftshift(result)
    # 为了显示频谱图，需要进一步操作将像素转换为0-255
    result = 20*np.log(np.abs(result))
    plt.subplot(121)
    plt.imshow(result)
    plt.title("fft_img")
    plt.axis('off')
    plt.subplot(122)
    plt.imshow(img)
    plt.title('img')
    plt.axis('off')
    plt.show()

效果如图：

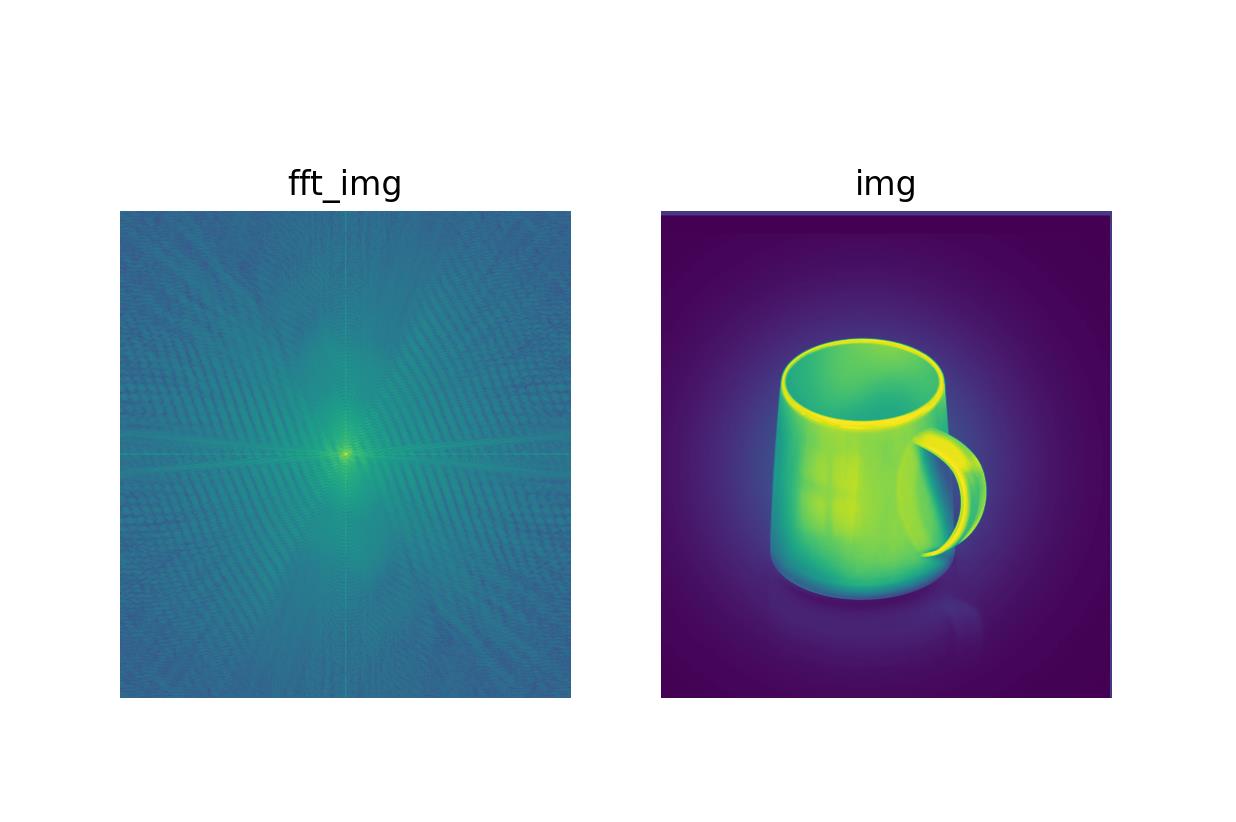
2、使用opencv进行傅里叶变换
函数体：cv2.dft() 傅里叶逆变换函数：cv2.idft()
需要注意的点：对于传入的参数图像，需要将其格式改变为float32型.
D对于转换标志参数flags，通常使用cv2.DFT_COMPLEX_OUTPUT

def cv_fft():
    img = cv.imread("car_red.jpg", 0)
    # 格式转换
    img = np.float32(img)
    result = cv.dft(img, flags=cv.DFT_COMPLEX_OUTPUT)
    # 将0频谱移动至图像中心
    result = np.fft.fftshift(result)
    print(result.shape)
    # 数值转换来完成显示  magnitude返回的是两个参数平方和的平方根
    cc = 20*np.log(cv.magnitude(result[:, :, 0], result[:, :, 1]))
    plt.subplot(122)
    plt.imshow(cc)
    plt.title("dft")
    plt.axis('off')
    plt.subplot(121)
    plt.imshow(img)
    plt.title('img')
    plt.axis('off')
    plt.show()

结果：

相比之下，使用numpy进行傅里叶变换的步骤更加少一些，因此可以直接使用numpy进行傅里叶操作，最后结果再用opencv显示。

3、傅里叶逆变换与图像滤波
在一幅图像内，同时存在着高频信号和低频信号。前面也提到其信号对于原图像中的特征。傅里叶变换可以将图像中的高频信号与低频信号分离，然后通过高通滤波或者低通滤波处理，可以实现图像增强、图像去噪、边缘提取、压缩和加密等操作。

def np_fft():
    img = cv.imread("car_red.jpg", cv.IMREAD_GRAYSCALE)
    # 获取图像中心点坐标
    row, col = img.shape
    center = [int(row/2), int(col/2)]
    # 傅里叶变换 ，0频率在左上角
    result = np.fft.fft2(img)
    # 将位于左上角的0频率移到图像中间
    result_f = np.fft.fftshift(result)
    # 将位于频谱中位于中间的低频信号的值变为0，逆变换后，对应图像变换缓慢区域的像素点将变为0
    result_f[center[0]-30:center[0]+30, center[1]-30:center[1]+30] = 0
    print(result_f)
    # 逆变换
    result_f = np.fft.ifftshift(result_f)
    i_img = np.abs(np.fft.ifft2(result_f))
    plt.subplot(122)
    plt.imshow(i_img, cmap='gray')
    plt.title('i_img')
    plt.axis('off')
    plt.subplot(121)
    plt.imshow(img, cmap='gray')
    plt.title('img')
    plt.axis('off')
    plt.show()

结果如图：

对傅里叶变换后的中心区域取0值，逆变换后，像素点变换平滑区域的值也变为0，保留了大部分的边缘信息。