算法设计与分析(屈婉玲)视频笔记day2

Posted 2023-03-14 林寻星辰

序列求和的方法

数列求和公式

等差、等比数列与调和级数

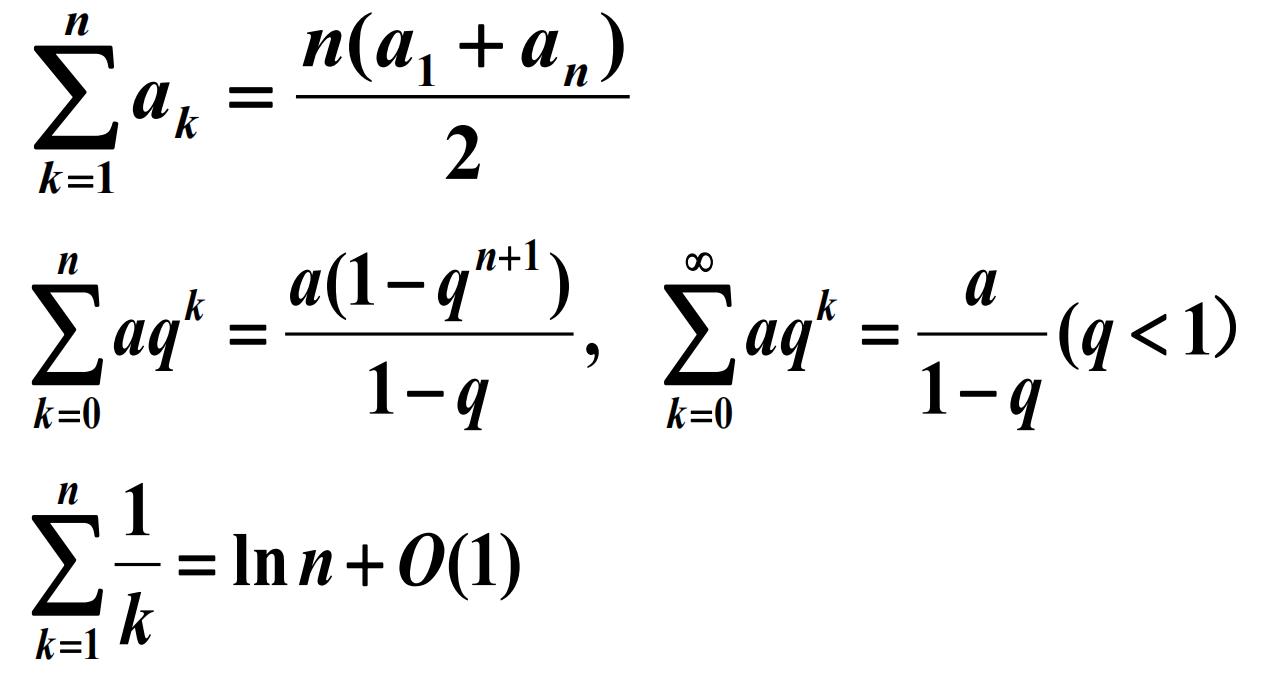
求和的例子

二分检索算法

二分检索运行实例

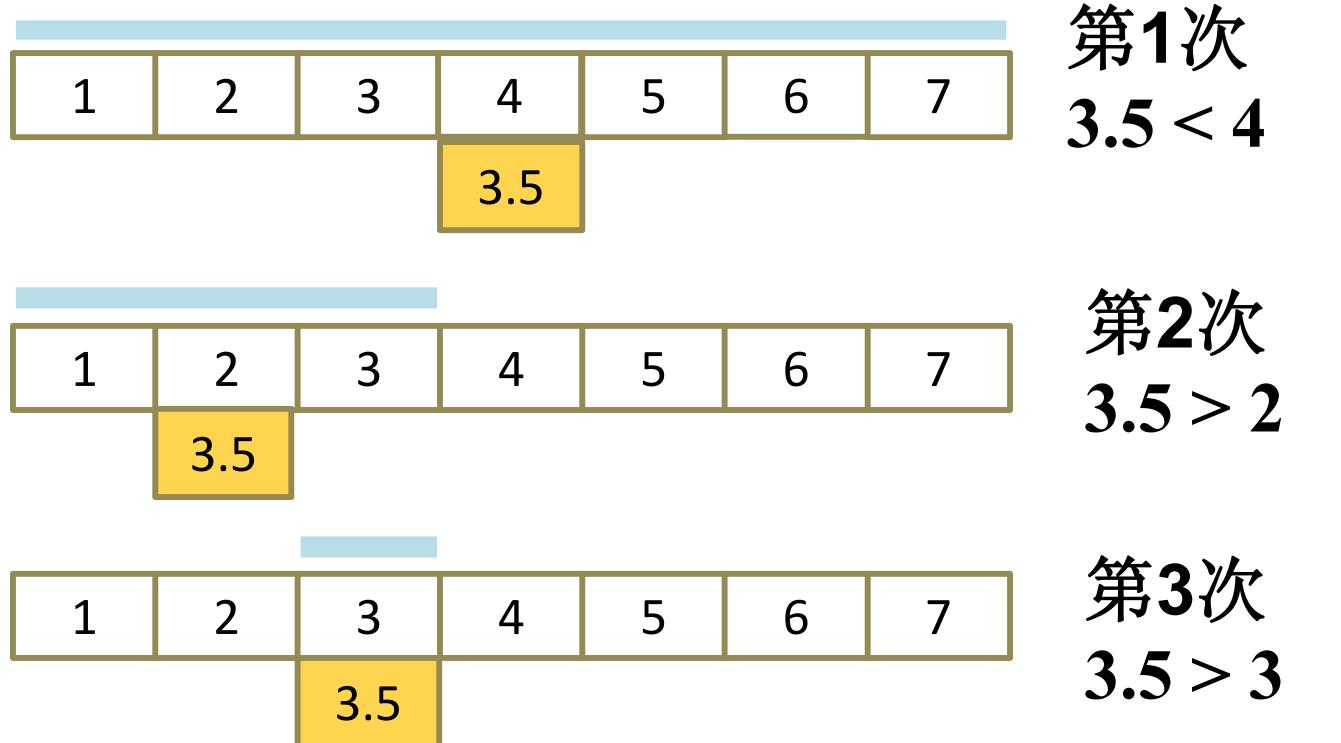
2 n +1个输入

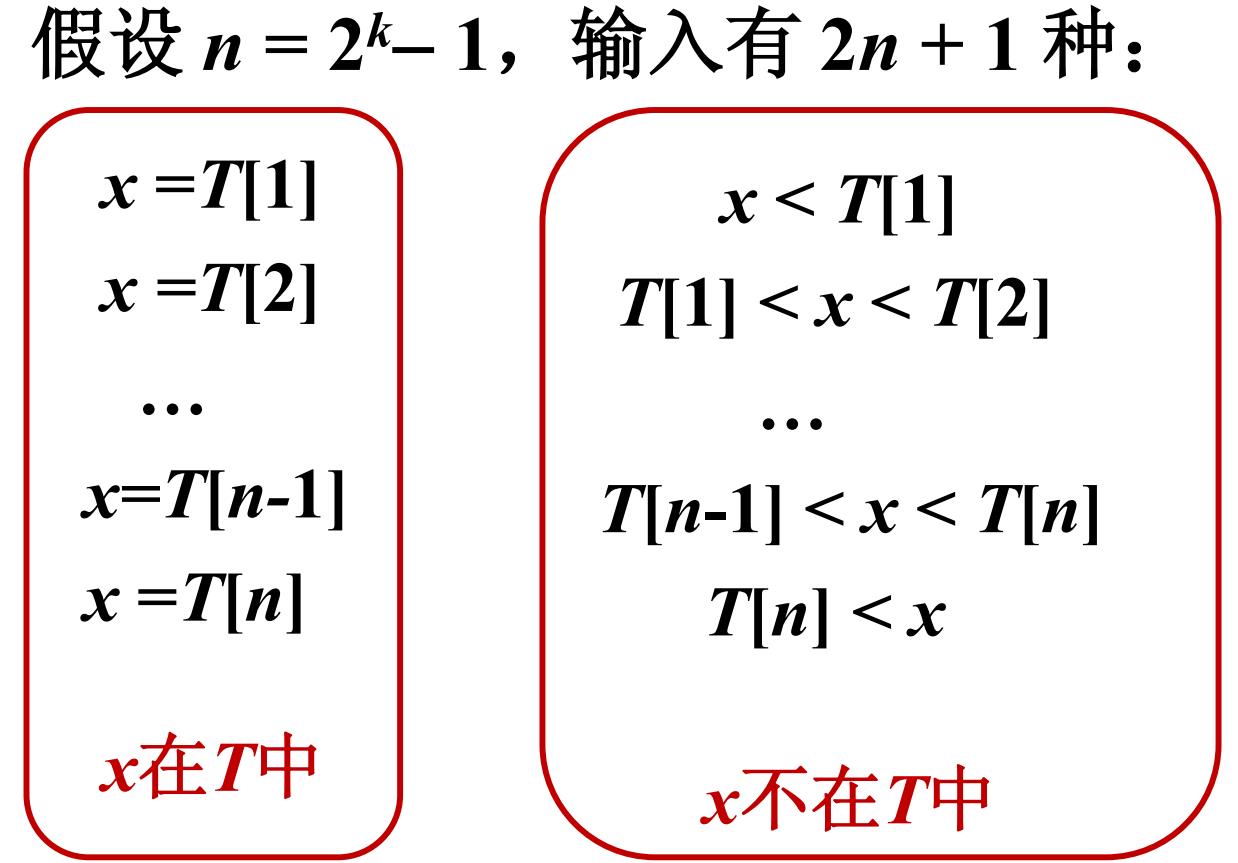
比较 t 次的输入个数

二分检索平均时间复杂度

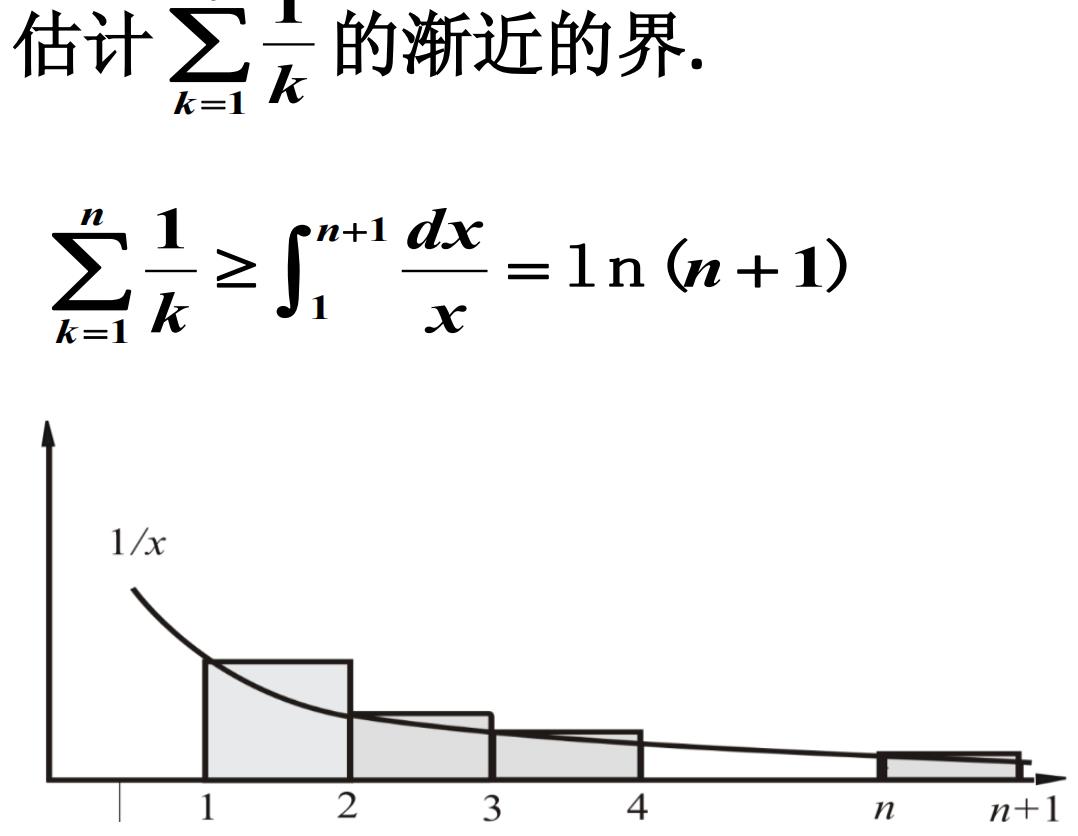
估计和式上界的放大法

放大法的例子

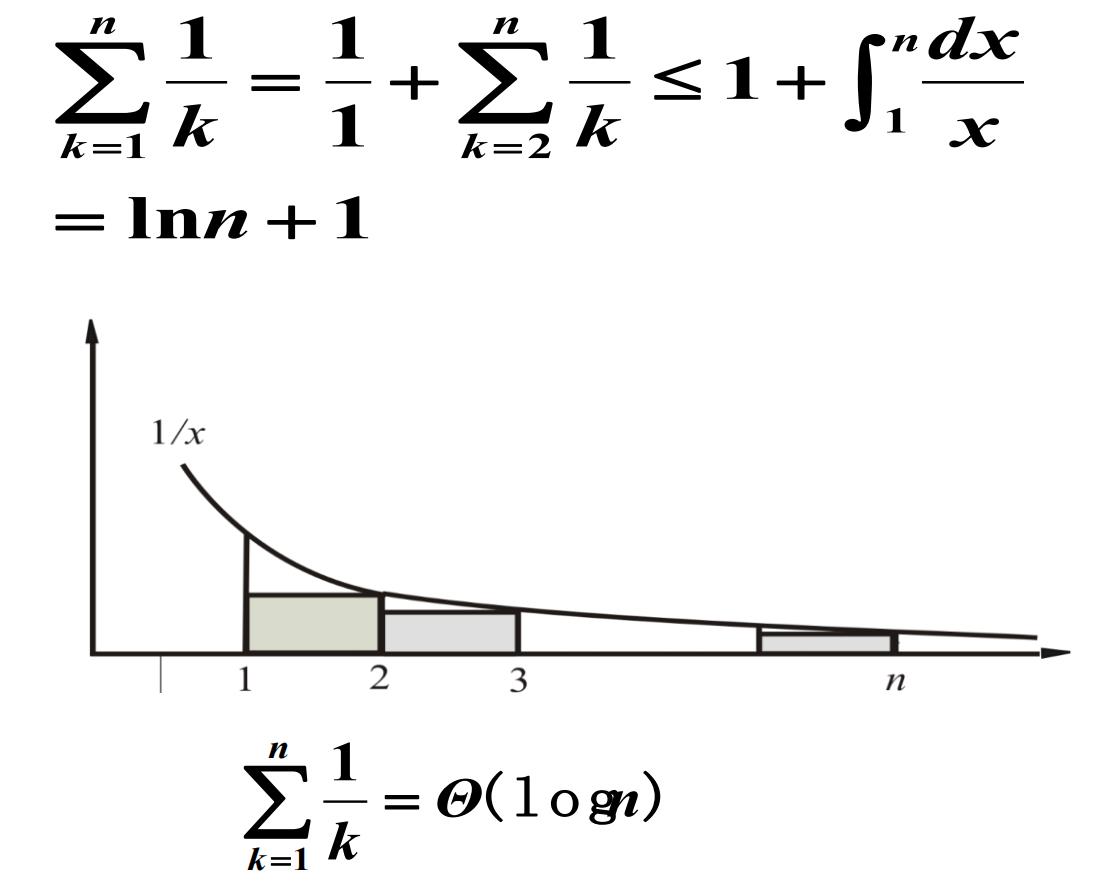
估计和式渐近的界

估计和式渐近的界

小结

• 序列求和基本公式：

等差数列

等比数列

调和级数

• 估计序列和：

放大法求上界

用积分做和式的渐近的界

• 应用：计数循环过程的基本运算次数

递推方程与算法分析

递推方程

递推方程的例子

Fibonacci数的存在

Hanoi塔问题

递归算法

分析算法

插入排序

最坏情况下时间复杂度

插入排序：

设基本运算是元素比较，对规模为 n

的输入最坏情况下的时间复杂度 W ( n )

W ( n )= W ( n -1)+ n -1 W (1)=0

解为 W ( n ) = n ( n -1)/2

小结

•递推方程的定义及初值

•递推方程与算法时间复杂度的关系

Hanoi塔的递归算法 插入排序的迭代算法

迭代法求解递推方程

迭代法

•不断用递推方程的右部替换左部

•每次替换，随着 n 的降低在和式中

多出一项

•直到出现初值停止迭代

•将初值代入并对和式求和

•可用数学归纳法验证解的正确性

Hanoi 塔算法

插入排序算法

换元迭代

•将对 n 的递推式换成对其他变元 k 的递推式

•对 k 直接迭代

•将解 (关于 k 的函数) 转换成关于 n 的函数

二分归并排序

MergeSort ( A , p , r )

输入：数组 A [ p … r ]

输出：按递增顺序排序的数组 A

1. if p < r

2. then q  ( p+r )/2 

3. MergeSort ( A , p , q )

4. MergeSort ( A , q +1, r )

换元

假设 n =2 k , 递推方程如下：

W ( n )=2 W ( n /2)+ n  1

W (1)=0

换元：

W (2 k ) = 2 W (2 k -1 ) + 2 k  1

W (0) = 0

迭代求解

解的正确性-归纳验证

证明 : 下述递推方程的解是 W ( n )= n ( n  1)/2

W ( n )= W ( n  1)+ n  1

W (1)=0

方法：数学归纳法

证 n =1 ， W (1)=1  (1  1)/2 = 0

假设对于 *n , *解满足方程，则

W ( n +1)

= W ( n )+ n = n ( n  1)/2 + n

= n [( n 1)/2+1] = n ( n +1)/2

小结

迭代法求解递推方程

• 直接迭代，代入初值，然后求和

• 对递推方程和初值进行换元，然

后求和，求和后进行相反换元，

得到原始递推方程的解

• 验证方法——数学归纳法

差消法化简高阶递推方程

快速排序

• 假设 A [ p … r ] 的元素彼此不等

以首元素 A [1] 对数组 A [ p…r ] 划分 , 使得：

小于 x 的元素放在 A [ p … q  1]

大于 x 的元素放在 A [ q +1… r ]

• 递归对 A [ p … q  1] 和 A [ q +1… r ] 排序

工作量： 子问题工作量+划分工作量

输入情况

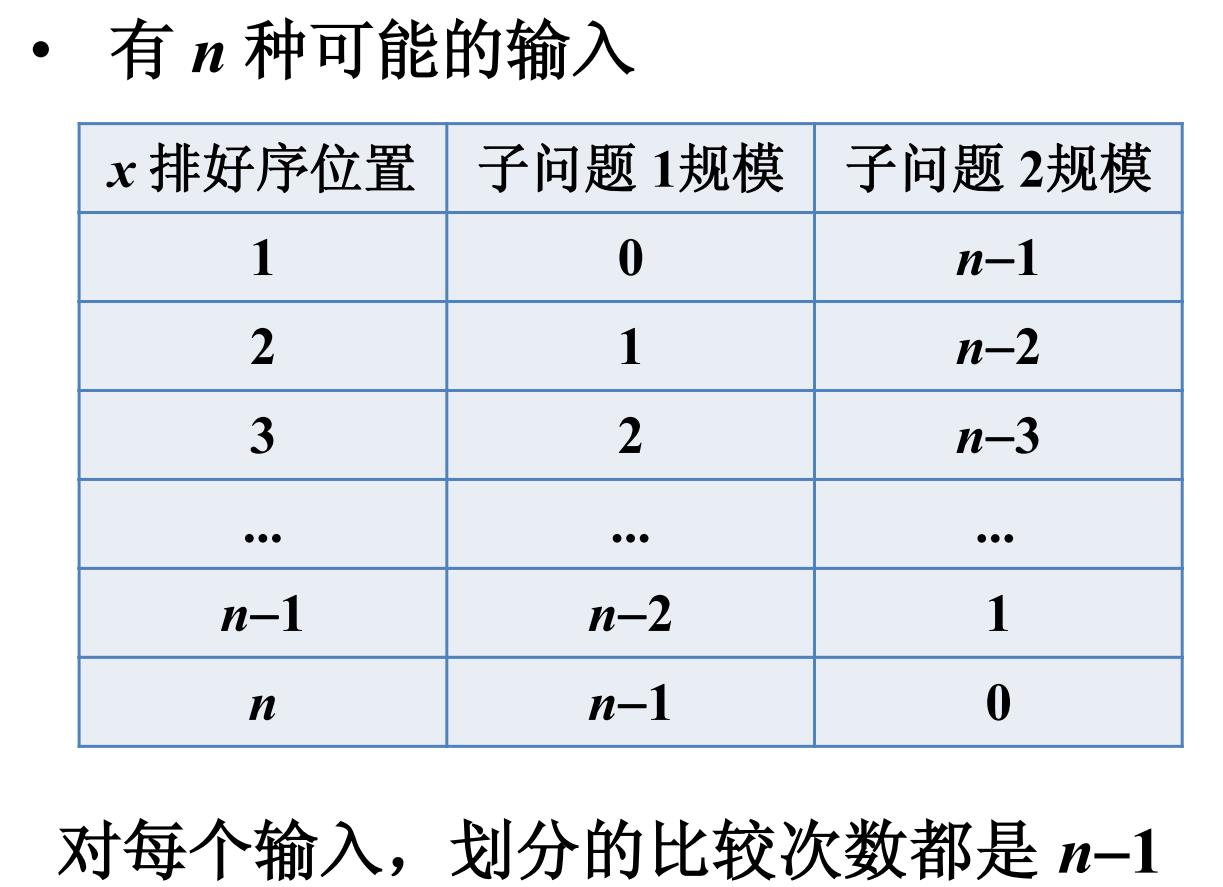
工作量总和

快速排序平均工作量

假设首元素排好序在每个位置是等

概率的

全部历史递推方程

对于高阶方程应该先化简，然后迭代

差消化简

利用两个方程相减，将右边的项尽可能

消去，以达到降阶的目的

差消化简

迭代求解

小结

• 对于高阶递推方程先要用差消法化简为一阶方程

• 迭代求解

递归树

有关基 递归树的概念 本概

• 递归树是迭代计算的模型 .

• 递归树的生成过程与迭代过程一致 .

• 递归树上所有项恰好是迭代之后产

生和式中的项 .

• 对递归树上的项求和就是迭代后方

程的解.

迭代在递归树中的表示

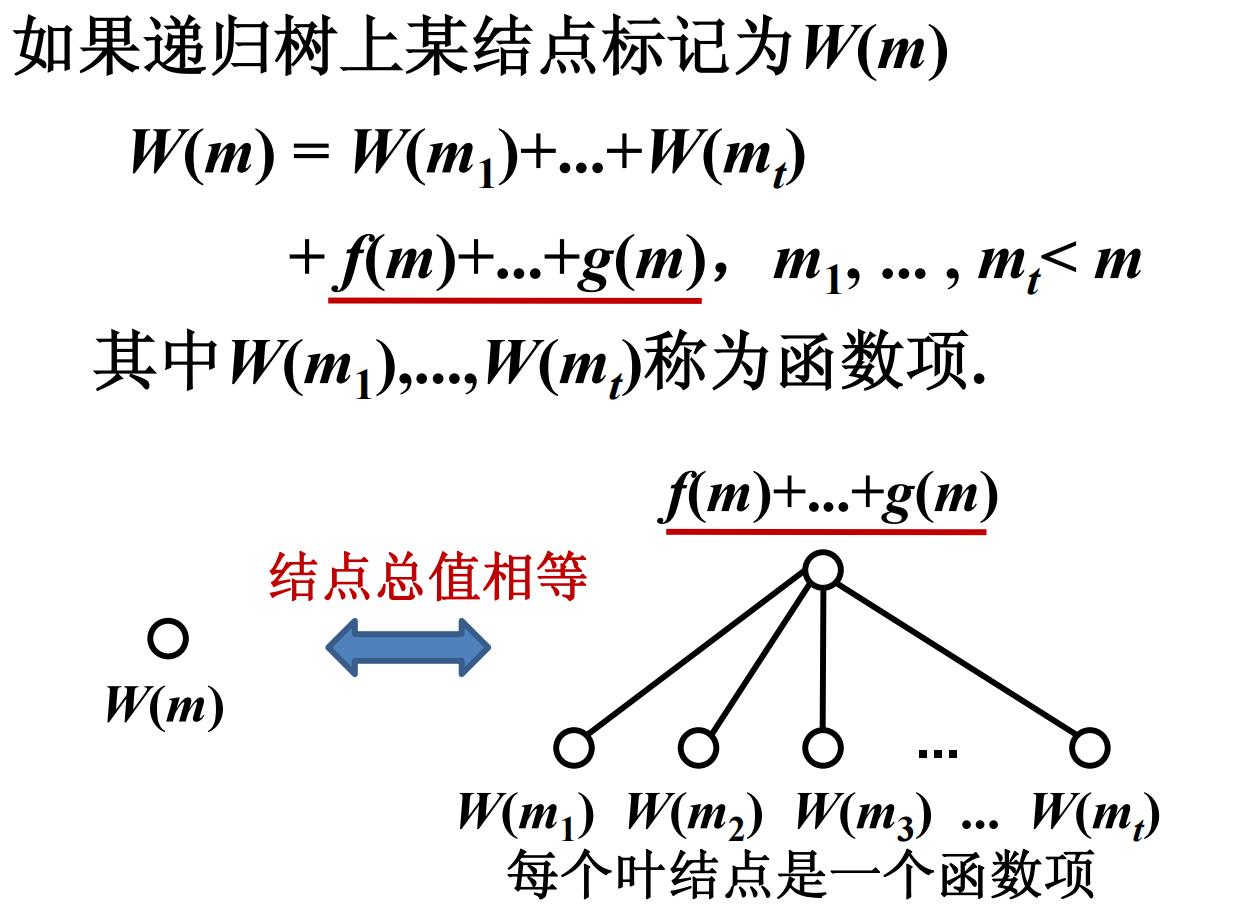
二层子树的例子

递归树的生成规则

• 初始，递归树只有根结点 , 其值为 W ( n )

• 不断继续下述过程：

将函数项叶结点的迭代式 W ( m ) 表示成二

层子树

用该子树替换该叶结点

• 继续递归树的生成，直到树中无函数项

(只有初值)为止.

递归树生成实例

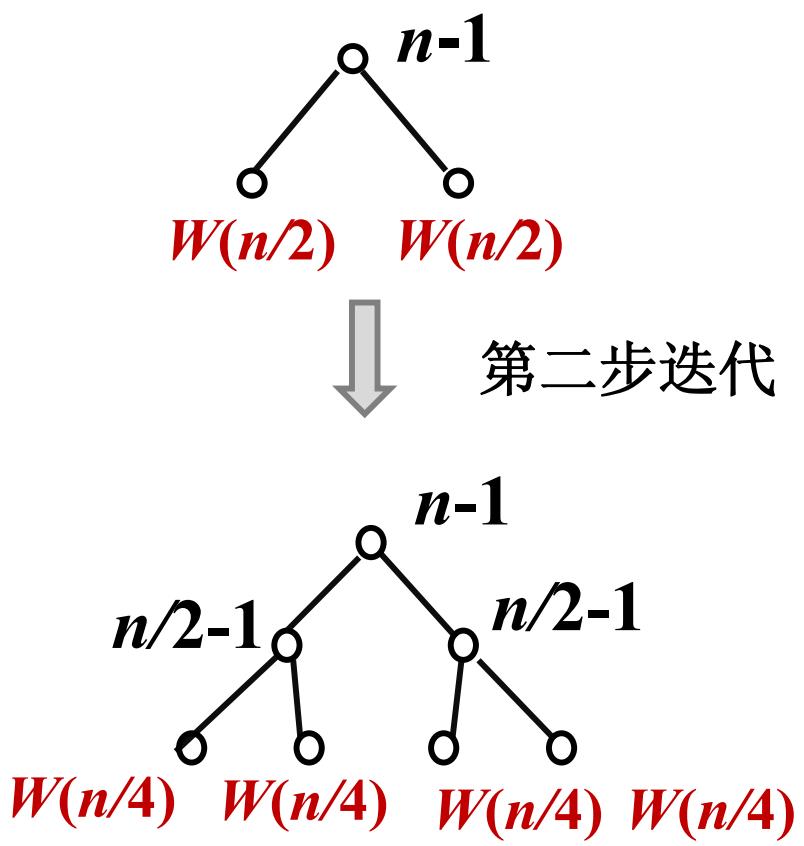
递归树

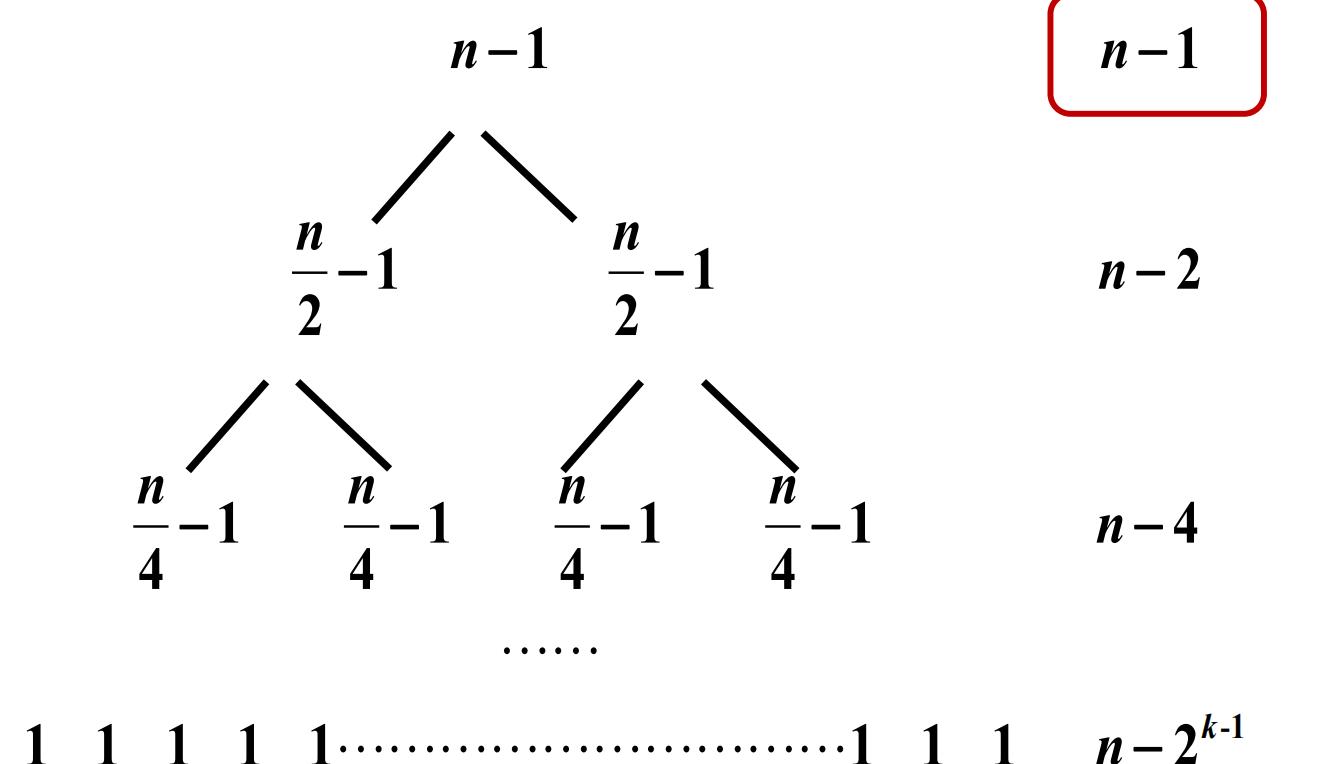
对递归树上的量求和

递归树应用实例

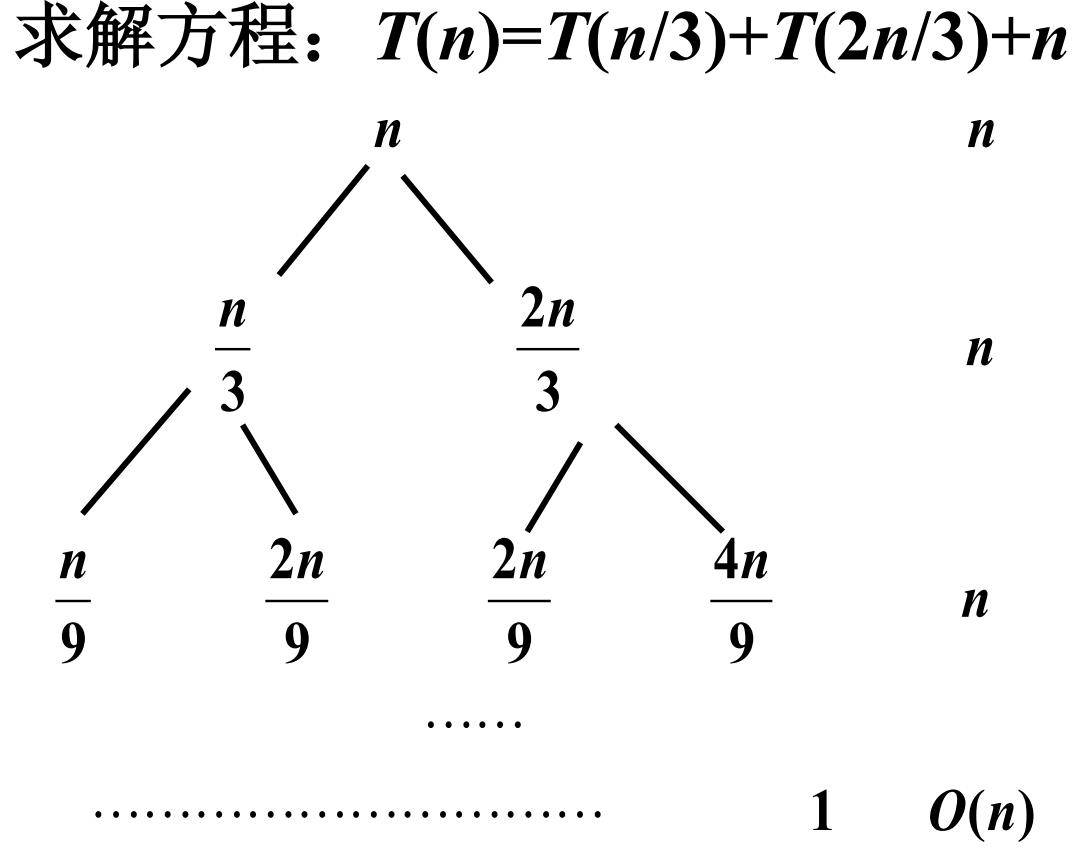
求和

方程： T ( n )= T ( n /3)+ T (2 n /3)+ n

递归树层数 k ，每层 O ( n )

******

小结

• 递归树是迭代的图形表述

• 递归树的生成规则

• 如何利用递归树求解递推方程?

主定理及其证明

主定理的应用背景

求解递推方程

T ( n ) = a T ( n / b ) + f ( n )

a ： 归约后的子问题个数

n/b ：归约后子问题的规模

f ( n ) ：归约过程及组合子问题的解的

工作量

二分检索： T ( n ) = T ( n /2)+1

二分归并排序： T ( n ) =2 T ( n /2)+ n -1

主定理

迭代

迭代结果

小结

• 主定理的应用背景

• 主定理的内容

• 主定理的证明

主定理的应用

求解递推方程：例1

例 1 求解递推方程

T ( n ) = 9 T ( n /3) + n

解 上述递推方程中的

a = 9 ， b = 3 ， f ( n ) = n

n log 3 9 = n 2 , f ( n ) = O ( n log 3 9-1 )

相当于主定理的 case1 ，其中  =1.

根据定理得到 T ( n ) =  ( n 2 )

求解递推放出:例2

例 2 求解递推方程

T ( n ) = T (2 n /3) + 1

****求解递推方程：例2

解 上述递推方程中的

a = 1, b = 3/2, f ( n ) = 1 ，

n log 3/2 1 = n 0 = 1

相当于主定理的

Case2 .

根据定理得到 T ( n ) =  ( log n )

条件验证

递归算法分析

不能使用主定理的例子

递归树求解

求和

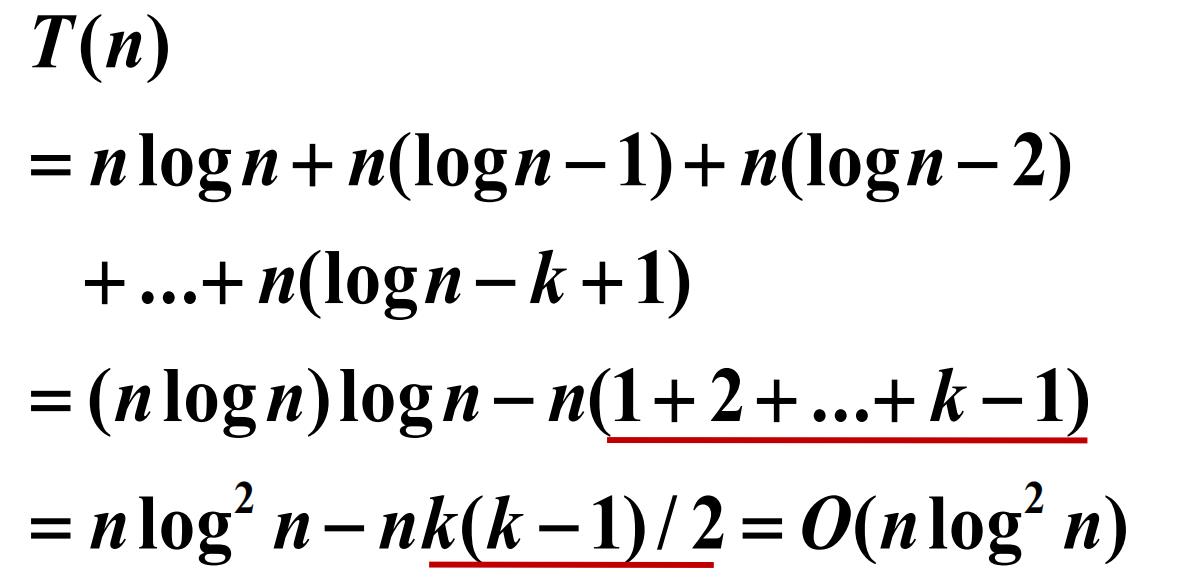
小结

• 使用主定理求解递推方程需要

满足什么条件？

• 主定理怎样用于算法复杂度分

析？