leetcode 834

Posted 2021-01-07 leohujx

题目链接

这道题目如果从暴力的角度来说，对于每个点，我们都可以去求其他所有点到这个点的距离之和，但是这样的话最后的算法复杂度就是O(N^2)了，题目中说n的范围是10000，所以我们明显不能用暴力的方法去做。这道题还是看了题解做出来的。

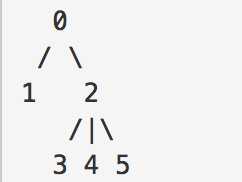
首先，这道题目是一道图的题目，不过按照题目的说法形成的是树，所以肯定是没有环的。这里我们需要以下几个数组结构来进行求解。

g数组，它用来构造图，是一个领接表。

sub_nodes数组，sub_nodes[i]代表的是某个节点的子节点数目(包括自身)，比如上图中sub_nodes[2]=3(3,4,5三个节点)

sub_dis数组，sub_dis[i]代表的是某个节点i的子节点到节点i的距离之和，如上图所示，sub_dis[2]的值为3(2到3，4，5的距离之和)，接下来推出子节点和父节点的关系，假设u是v的父节点，那么sub_dis[u] = sub_dis[v] + sub_nodes[v]*1，比如0是2的父节点(先撇开0的左子树不管)，那么0的子节点到它的和应该是2的子节点到它的和 加上 2的子节点数*1， 即 sub_dis[0] = sub_dis[2] + sub_nodes[2]*1 = 3 + 3*1 = 6。

sum_dis数组，这个数组就是我们最后要求的，sum_dis[i]代表其它所有节点到i节点的距离之和。假设0是根节点，那么能够看出来sum_dis[0]=sub_dis[0]。对于一般的父节点u和子节点v来说，如果已知sum_dis[u]，那么对于v来说，所有其它点到它的距离之和是 所有点到u的距离之和 减去 v的子节点数目*1(相当于子节点到v不需要经过u->v这条路径，所以减去) 加上 其它非v的子节点的数目*1(即其它非子节点到v需要经过u->v这条路径)，即 sum_dis[v] = sum_dis[u] - sub_nodes[v]*1 + (N-sub_nodes[v])*1。

从上面可以看出来，sub_nodes和sub_dis的数组是需要从下往上更新，而由于sum_dis[0]是已知的(sum_dis[0]=sub_dis[0])，那么应该是从上往下更新，写成两个dfs即可。

class Solution {
public:
    vector<int> sumOfDistancesInTree(int N, vector<vector<int>>& edges) {
        vector<vector<int>> g(N+1); //图
        vector<int> sub_dis(N+1, 0);  //sub_dis[i]代表某个节点i的子节点到它的距离之和
        vector<int> sub_nodes(N+1, 0); //sub_nodes[i]代表某个节点i的子节点数目
        vector<int> sum_dis(N, 0); //sum_dis[i]就代表其他所有点到i点的距离之和
        int n = (int)edges.size();
        for(int i=0;i<n;i++){
            int u = edges[i][0];
            int v = edges[i][1];
            g[u].push_back(v);
            g[v].push_back(u);
        }
        dfs1(0, 0, g, sub_dis, sub_nodes);
        sum_dis[0] = sub_dis[0];
        dfs2(0, 0, N, g, sub_dis, sub_nodes, sum_dis);
        return sum_dis;
    }
    
    void dfs1(int u, int fa, vector<vector<int>>& g, vector<int>& sub_dis, vector<int> &sub_nodes){
        sub_dis[u] = 0;
        sub_nodes[u] = 1;
        for(int i=0;i<(int)g[u].size();i++){
            int v = g[u][i];
            if(v == fa) continue;
            dfs1(v, u, g, sub_dis, sub_nodes);
            sub_dis[u] += sub_dis[v] + sub_nodes[v]*1;
            sub_nodes[u] += sub_nodes[v];
        }
    }
    
    void dfs2(int u,int fa, int N, vector<vector<int>>& g, vector<int>& sub_dis, vector<int> &sub_nodes, vector<int>& sum_dis){
        for(int i=0;i<(int)g[u].size();i++){
            int v = g[u][i];
            if(v == fa) continue;
            sum_dis[v] = sum_dis[u] - sub_nodes[v]*1 + (N-sub_nodes[v])*1;
            dfs2(v, u, N, g, sub_dis, sub_nodes, sum_dis);
        }
    }    
};