[leetcode] 221. 最大正方形

Posted 2020-12-27 ACBingo

221. 最大正方形

其实这题是85. 最大矩形的特殊情况，我们将85题代码稍微改一下，然后直接套用即可。

此题要求是正方形，那么我们在计算长与宽时，取短的那条然后平方即可。

class Solution {
    public int maximalSquare(char[][] matrix) {
        return maximalRectangle(matrix);
    }

    public int maximalRectangle(char[][] matrix) {
        int m = matrix.length;
        if (m == 0) return 0;
        int n = matrix[0].length;
        if (n == 0) return 0;

        int[] height = new int[n];
        int ans = 0;

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == \'0\') height[j] = 0;
                else if (matrix[i][j] == \'1\') height[j] += 1;
            }
            ans = Math.max(largestRectangleArea(height), ans);
        }
        return ans;
    }

    public int largestRectangleArea(int[] heights) {
        if (heights.length == 0) return 0;
        Stack<Integer> stack = new Stack<>();

        int max = 0;
        for (int i = 0; i < heights.length; i++) {
            while (!stack.isEmpty() && heights[stack.peek()] >= heights[i]) {
                int tmp = stack.pop();
                // 把当前的tmp木板作为最短木板，看能组成的最大面积是多少
                int bian = Math.min(heights[tmp], (stack.empty() ? i : i - stack.peek() - 1));
//                max = Math.max(max, heights[tmp] * (stack.empty() ? i : i - stack.peek() - 1));
                max = Math.max(max, bian * bian);
            }
            stack.push(i);
        }

        int tmp = 0;
        int len = heights.length;
        while (!stack.isEmpty()) {
            tmp = stack.pop();
            int bian = Math.min(heights[tmp], (stack.empty() ? len : len - stack.peek() - 1));
//            max = Math.max(max, heights[tmp] * (stack.empty() ? len : len - stack.peek() - 1));
            max = Math.max(max, bian * bian);
        }

        return max;
    }
}

另外，这个题可以用dp来做。思路还是很巧妙的。

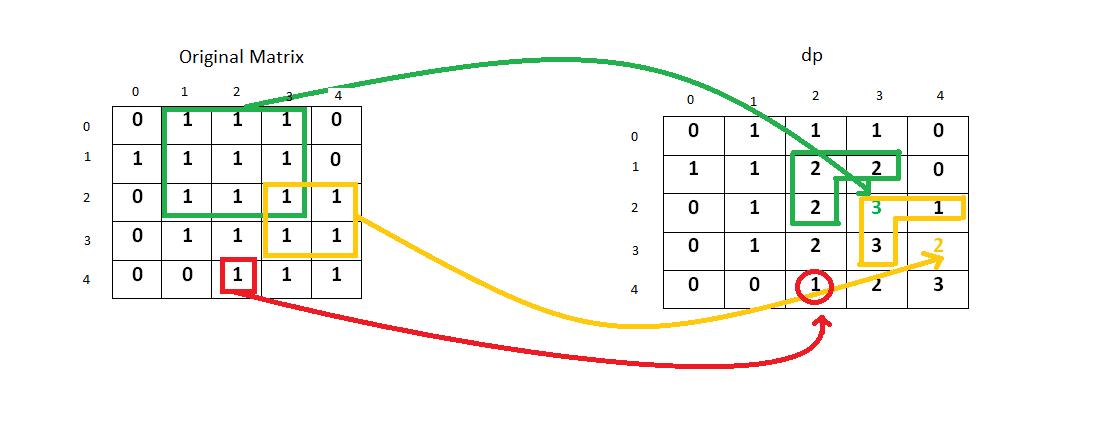
dp[i,j]表示以（i，j）为右下角的矩阵的面积，那么状态转移方程为：
如果（i,j）为1，dp[i,j] = min (dp[i-1,j],dp[i-1,j-1],d[i,j-1])+1;
也就是说，dp(i,j)只看其身边三个点的状态即可

大家可以看图，自己从图一0，0点开始推下，推几个点就想明白了