105. 从前序与中序遍历序列构造二叉树
题目
难度中等534
根据一棵树的前序遍历与中序遍历构造二叉树。
注意:
你可以假设树中没有重复的元素。
例如,给出
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树:
3
/ \\
9 20
/ \\
15 7
思路
首先要知道,前序遍历和中序遍历的意义。
前序遍历是将一棵树 根-> 左 -> 右 (节点) 进行遍历
而后序遍历是将一棵树 左->根->右 (节点)进行遍历
由这两个特性我们可以得到一个结论。
前序遍历的第一个节点是根节点,而中序遍历中以根节点为划分,其左边为左子树,右边为右子树。可以画图来说明:
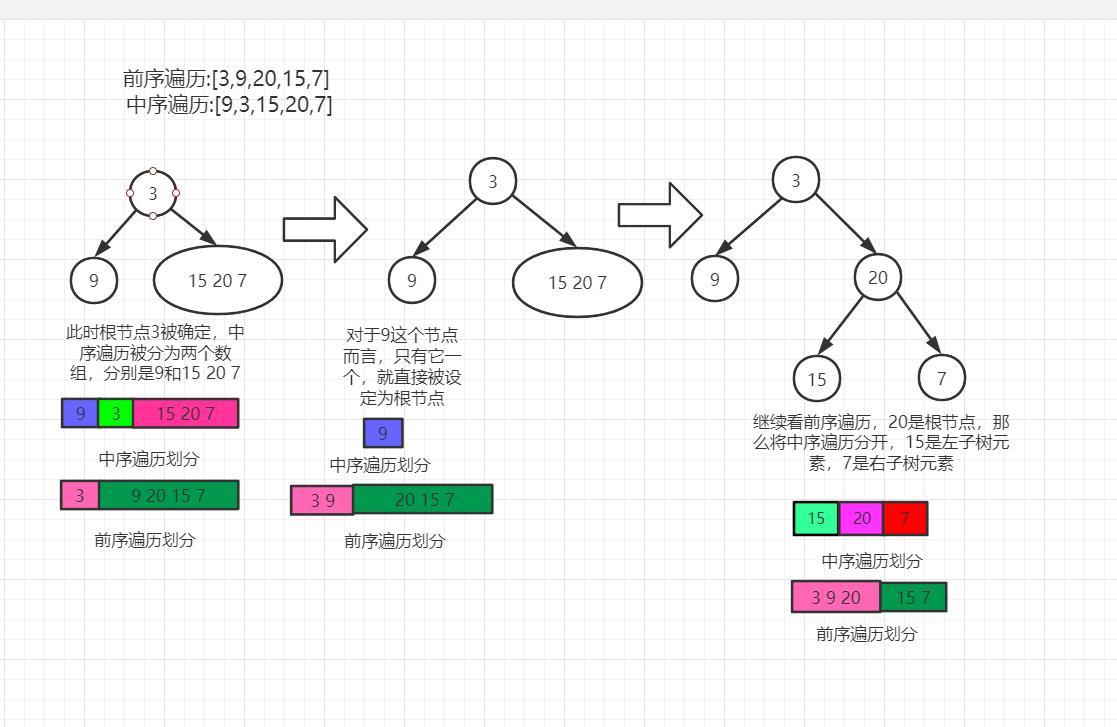
结合图片,再利用递归即可轻松解出这道题目
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
int k = 0;
public TreeNode buildTree(int[] preorder, int[] inorder) {
// 前序遍历, 根左右
// 中序遍历, 左根右
// 所以由前序遍历可以确定根节点
// 由中序遍历判断左右子树
// 可以使用递归的方法每次生成当前根节点,然后再通过中序遍历找到左右子树分界点,然后再递归进入
// 终止条件是传入的中序遍历没有元素了.
return recursionBuildTree(preorder, inorder, 0, inorder.length-1);
}
// 前序遍历
// 中序遍历
// 数组左界限 [
// 数组右界限 ]
TreeNode recursionBuildTree(int[] preorder, int[] inorder, int left, int right){
if (left > right){
return null;
}
// 获取当前树根节点的值
int root = preorder[k];
k++;
// 建立根节点
TreeNode treeRoot = new TreeNode(root);
// 找到左右子树的分界点
int mid = 0;
for(int i=left; i<=right; i++){
if(root == inorder[i])
{
mid = i;
break;
}
}
// 获取左子树
treeRoot.left = recursionBuildTree(preorder, inorder, left, mid-1);
// 获取右子树
treeRoot.right = recursionBuildTree(preorder,inorder, mid+1, right);
return treeRoot;
}
}