精确率和召回率
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了精确率和召回率相关的知识,希望对你有一定的参考价值。
参考技术A 机器学习(ML),自然语言处理(NLP),信息检索(IR)等领域,评估(Evaluation)是一个必要的 工作,而其评价指标往往有如下几点:准确率(Accuracy),精确率(Precision),召回率(Recall)和F1-Measure。TP: Ture Positive 把正的判断为正的数目 True Positive,判断正确,且判为了正,即正的预测为正的。
FN: False Negative 把正的错判为负的数目 False Negative,判断错误,且判为了负,即把正的判为了负的
FP: False Positive 把负的错判为正的数目 False Positive, 判断错误,且判为了正,即把负的判为了正的
TN: True Negative 把负的判为负的数目 True Negative,判断正确,且判为了负,即把负的判为了负的
【举例】一个班里有男女生,我们来进行分类,把女生看成正类,男生看成是负类。我们可以用混淆矩阵来描述TP、TN、FP、FN。
混淆矩阵
相关(Relevant),正类 无关(NonRelevant),负类
被检索到(Retrieved) True Positives(TP,正类判定为正类。即女生是女生) False Positives(FP,负类判定为正类,即“存伪”。男生判定为女生)
未被检索到(Not Retrieved) False Negatives(FN,正类判定为负类,即“去真”。女生判定为男生) True Negatives(TN,负类判定为负类。即男生判定为男生)
1. 准确率 (Accuracy)
准确率是指有在所有的判断中有多少判断正确的,即把正的判断为正的,还有把负的判断为负的;总共有 TP + FN + FP + TN 个,所以准确率:Acc = (TP+TN) / (TP+TN+FN+FP)
2. 精确率(Precision)
精确率是相对于预测结果而言的,它表示的是预测为正的样本中有多少是对的;那么预测为正的样本就有两种可能来源,一种是把正的预测为正的,这类有TruePositive个, 另外一种是把负的错判为正的,这类有FalsePositive个,因此精确率即:P= TP / (TP+FP)
3. 召回率 (Recall)
召回率是相对于样本而言的,即样本中有多少正样本被预测正确了,这样的有TP个,所有的正样本有两个去向,一个是被判为正的,另一个是错判为负的,因此总共有TP+FN个,所以,召回率 R= TP / (TP+FN)
我们当然希望检索的结果P越高越好,R也越高越好,但事实上这两者在某些情况下是矛盾的。比如极端情况下,我们只搜出了一个结果,且是准确的,那么P就是100%,但是R就很低;而如果我们把所有结果都返回,那么必然R是100%,但是P很低。因此在不同的场合中需要自己判断希望P比较高还是R比较高。如果是做实验研究,可以绘制Precision-Recall曲线来帮助分析。
4.F-Measure
P和R指标有的时候是矛盾的,那么有没有办法综合考虑他们呢?我想方法肯定是有很多的,最常见的方法应该就是F-Measure了
F-Measure是Precision和Recall加权调和平均:
当参数a=1时,就是最常见的F1了:
F1综合了P和R的结果,当F1较高时则比较说明实验方法比较理想。将Precision和Recall的上述公式带入会发现,当F1值小时,True Positive相对增加,而false相对减少,即Precision和Recall都相对增加,即F1对Precision和Recall都进行了加权。
分类算法-2.精准率和召回率曲线
精准率和召回率是两个不同的评价指标,很多时候它们之间存在着差异,具体在使用的时候如何解读精准率和召回率,应该视具体使用场景而定
有些场景,人们可能更注重精准率,如股票预测系统,我们定义股票升为1,股票降为0,我们更关心的是未来升的股票的比例,而在另外一些场景中,人们更加注重召回率,如癌症预测系统,定义健康为1,患病为0,我们更关心癌症患者检查的遗漏情况。
F1 Score
F1 Score 兼顾精准率和召回率,它是两者的调和平均值
[frac{1}{F1} = frac{1}{2}(frac{1}{Precision} + frac{1}{recall})]
[F1 = frac{2cdot precisioncdot recall}{precision+recall}]
定义F1 Score
def f1_score(precision,recall):
try:
return 2*precision*recall/(precision+recall)
except:
return 0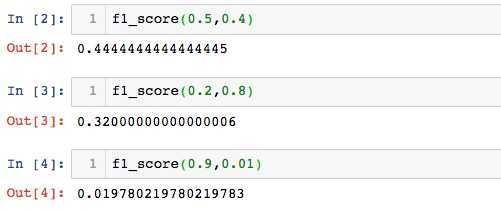
由上看出,F1 Score更偏向于分数小的那个指标
Precision-Pecall的平衡
精准率和召回率是两个互相矛盾的目标,提高一个指标,另一个指标就会不可避免的下降。如何达到两者之间的一个平衡呢?
回忆逻辑回归算法的原理:将一个结果发生的概率大于0.5,就把它分类为1,发生的概率小于0.5,就把它分类为0,决策边界为:( heta ^T cdot X_b = 0)
这条直线或曲线决定了分类的结果,平移决策边界,使( heta ^T cdot X_b)不等于0而是一个阈值:( heta ^T cdot X_b = threshold)
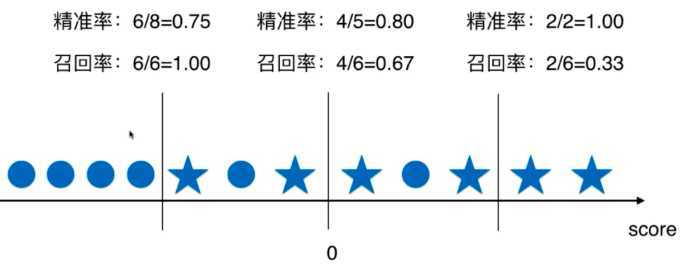
圆形代表分类结果为0,五角星代表分类结果为1,由上图可以看出,精准率和召回率是两个互相矛盾的指标,随着阈值的逐渐增大,召回率逐渐降低,精准率逐渐增大。
编程实现不同阀值下的预测结果及混淆矩阵
from sklearn.linear_model import LogisticRegression
# 数据使用前一节处理后的手写识别数据集
log_reg = LogisticRegression()
log_reg.fit(x_train,y_train)求每个测试数据在逻辑回归算法中的score值:
decision_score = log_reg.decision_function(x_test)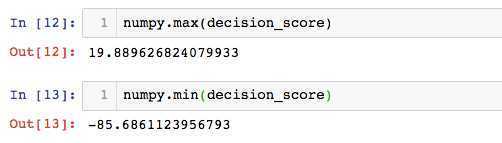
不同阀值下预测的结果
y_predict_1 = numpy.array(decision_score>=-5,dtype='int')
y_predict_2 = numpy.array(decision_score>=0,dtype='int')
y_predict_3 = numpy.array(decision_score>=5,dtype='int')查看不同阈值下的混淆矩阵:

精准率-召回率曲线
求出0.1步长下,阈值在[min,max]区间下的精准率和召回率,查看其曲线特征:
threshold_scores = numpy.arange(numpy.min(decision_score),numpy.max(decision_score),0.1)
precision_scores = []
recall_scores = []
# 求出每个分类阈值下的预测值、精准率和召回率
for score in threshold_scores:
y_predict = numpy.array(decision_score>=score,dtype='int')
precision_scores.append(precision_score(y_test,y_predict))
recall_scores.append(recall_score(y_test,y_predict))画出精准率和召回率随阈值变化的曲线
plt.plot(threshold_scores,precision_scores)
plt.plot(threshold_scores,recall_scores)
plt.show()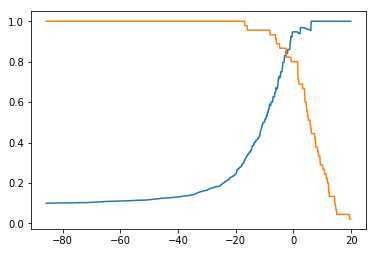
画出精准率-召回率曲线
plt.plot(precision_scores,recall_scores)
plt.show()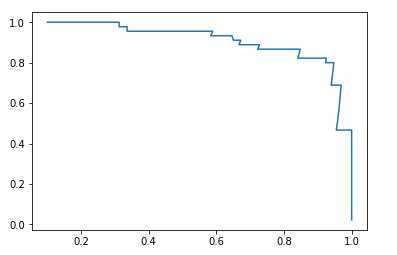
sklearn中的精准率-召回率曲线
from sklearn.metrics import precision_recall_curve
precisions,recalls,thresholds = precision_recall_curve(y_test,decision_score)
# sklearn中最后一个精准率为1,召回率为0,没有对应的threshold
plt.plot(thresholds,precisions[:-1])
plt.plot(thresholds,recalls[:-1])
plt.show()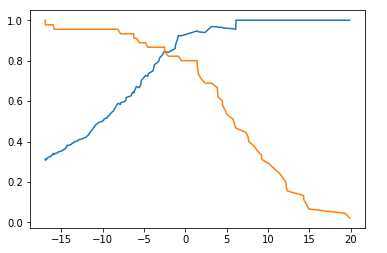
以上是关于精确率和召回率的主要内容,如果未能解决你的问题,请参考以下文章
准确率(Accuracy) 精确率(Precision) 召回率(Recall)和F1-Measure(精确率和召回率的调和平均值)