给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
- 所有数字(包括
target)都是正整数。 - 解集不能包含重复的组合。
示例 1:
输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
]
示例 2:
输入: candidates = [2,3,5], target = 8,
所求解集为:
[
[2,2,2,2],
[2,3,3],
[3,5]
]
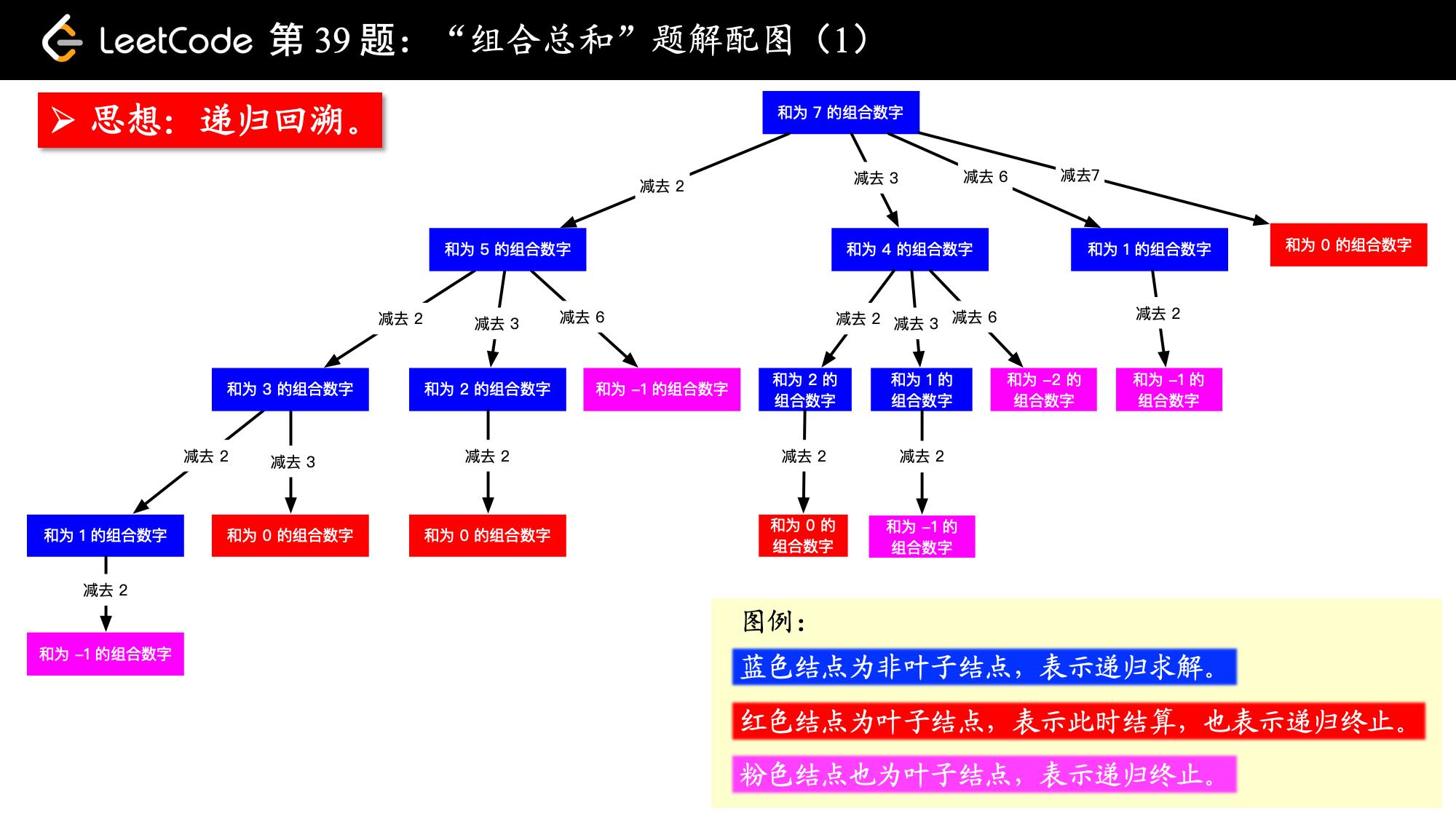
递归函数
这里我们新加入三个变量,start 记录当前的递归到的下标,out 为一个解,res 保存所有已经得到的解,每次调用新的递归函数时,此时的 target 要减去当前数组的的数,具体看代码如下:
c++
class Solution {
public:
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
vector<vector<int>> res;
vector<int> out;
combinationSumDFS(candidates, target, 0, out, res);
return res;
}
void combinationSumDFS(vector<int>& candidates, int target, int start, vector<int>& out, vector<vector<int>>& res) {
if (target < 0) return;
if (target == 0) {res.push_back(out); return;}
for (int i = start; i < candidates.size(); ++i) {
out.push_back(candidates[i]);
combinationSumDFS(candidates, target - candidates[i], i, out, res);
out.pop_back();
}
}
};
递归改进
我们也可以不使用额外的函数,就在一个函数中完成递归,还是要先给数组排序,然后遍历,如果当前数字大于 target,说明肯定无法组成 target,由于排过序,之后的也无法组成 target,直接 break 掉。如果当前数字正好等于 target,则当前单个数字就是一个解,组成一个数组然后放到结果 res 中。
然后将当前位置之后的数组取出来,调用递归函数,注意此时的 target 要减去当前的数字,然后遍历递归结果返回的二维数组,将当前数字加到每一个数组最前面,然后再将每个数组加入结果 res 即可,参见代码如下:
c++
class Solution {
public:
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
vector<vector<int>> res;
sort(candidates.begin(), candidates.end());
for (int i = 0; i < candidates.size(); ++i) {
if (candidates[i] > target) break;
if (candidates[i] == target) {res.push_back({candidates[i]}); break;}
vector<int> vec = vector<int>(candidates.begin() + i, candidates.end());
vector<vector<int>> tmp = combinationSum(vec, target - candidates[i]);
for (auto a : tmp) {
a.insert(a.begin(), candidates[i]);
res.push_back(a);
}
}
return res;
}
};
java
class Solution {
List<List<Integer>> res = new ArrayList<>();
public List<List<Integer>> combinationSum(int[] candidates, int target) {
if (target <= 0) {res.add(new ArrayList<>());}
//先排序,排序后可以加剪枝
Arrays.sort(candidates);
dfs(new ArrayList<>(), candidates, 0, target, 0);
return res;
}
public void dfs(List<Integer> list, int[] candidates, int sum, int target, int start) {
for (int i = start; i < candidates.length; i++) {
list.add(candidates[i]);
if ((sum + candidates[i]) == target) {
//此时tmpList 满足
List<Integer> tmpList = new ArrayList<>(list);
res.add(tmpList);
} if ((sum + candidates[i]) < target) {
dfs(list, candidates, sum + candidates[i], target, i);
} else {
list.remove(list.size() - 1);
//(sum+candidates[i]) > target,因为数组有序,后面一定不满足
break;
}
list.remove(list.size() - 1);
}
}
}
动态规划
我们也可以用迭代的解法来做,建立一个三维数组 dp,这里 dp[i] 表示目标数为 i+1 的所有解法集合。这里的i就从1遍历到 target 即可,对于每个i,都新建一个二维数组 cur,然后遍历 candidates 数组,如果遍历到的数字大于i,说明当前及之后的数字都无法组成i,直接 break 掉。否则如果相等,那么把当前数字自己组成一个数组,并且加到 cur 中。否则就遍历 dp[i - candidates[j] - 1] 中的所有数组,如果当前数字大于数组的首元素,则跳过,因为结果要求是要有序的。否则就将当前数字加入数组的开头,并且将数组放入 cur 之中即可,参见代码如下:
c++
class Solution {
public:
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
vector<vector<vector<int>>> dp;
sort(candidates.begin(), candidates.end());
for (int i = 1; i <= target; ++i) {
vector<vector<int>> cur;
for (int j = 0; j < candidates.size(); ++j) {
if (candidates[j] > i) break;
if (candidates[j] == i) {cur.push_back({candidates[j]}); break;}
for (auto a : dp[i - candidates[j] - 1]) {
if (candidates[j] > a[0]) continue;
a.insert(a.begin(), candidates[j]);
cur.push_back(a);
}
}
dp.push_back(cur);
}
return dp[target - 1];
}
};