Leetcode——2 Range Sum Query - Mutable（树状数组实现）

Posted 2020-08-21 真的是从入门开始

Problem：

Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive.

The update(i, val) function modifies nums by updating the element at index i to val.

 

Example:

Given nums = [1, 3, 5]

sumRange(0, 2) -> 9
update(1, 2)
sumRange(0, 2) -> 8

Analysis：

　　一开始想着用一个简单的数组存取并进行更新和求和就可以，实际写的时候发现不太可行，网上找了找发现了一种新的数据结构或者说一种新的方法——树状数组（Binary Index Tree ,or Fenwick Tree）。

　　树状数组常用于修改某点的值、求某个区间的和。普通数组修改某点值时间复杂度是O（1），查询的时间复杂度是O（n），对于树状数组来说修改和查询的时间复杂度都是O（logn）。

　　Reference——http://blog.csdn.net/int64ago/article/details/7429868

　　

 

 　　树状数组是巧妙地利用了二分，先介绍两个个“工具”——lowbit（k）和“加尾”操作。

　　lowbit（k）就是把k的二进制高位全部清0，只留下最低位1，如lowbit（0101）=0001，实现：lowbit（k）=k&（-k）。

　　加尾操作，把一个数k加上它自己的lowbit（k），k=k+lowbit（k），如去尾（0011）=0011+lowbit（0011）=0100。

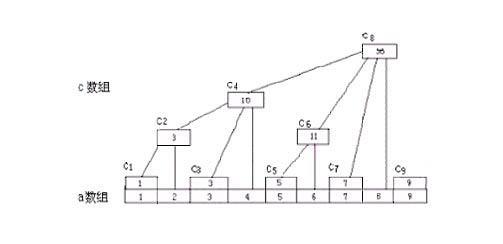
　　对a数组进行“操作”实际上是对c数组进行操作，也就是说我们正真用到的是c数组，那么c和a之间有某种关系，首先我们要找到这种关系，这就要用到第一个工具lowbit（k）。c[k]=a[k]向左边求lowbit（k）个和，比如c[0110]=a[0110]向左边求lowbit（0110）个和，也就是向左求两个和，则c[0110]=a[0110]+a[0101]。由这种方法就可以确定ck是由a中哪几个元素确定，如上图。

　　上面说的是如何由c找到对应的a，那么由a找到对应的c就要用到加尾操作，因为如果我们要对a中某个值进行更改，c中的值肯定也要对应更改，所以要找到a对应的所有c。如a[0011]对应的c，加尾（0011）=0011+lowbit（0011）=0100，加尾（0100）=0100+lowbit（0100）=1000，所以a[0011]对应3个c，c[0011],c[0100],c[1000]。

　　由右边的图我们可以更直观地看出对应关系，如c4直接包含了c2，c3（a3），c4（a4）（直接包括的黑方块），而c2直接包含了a1，a2，那么c4就包含了a1~a4，再如c6，包含了c6（a6），c5（a5）。

　　a和c的对应关系就是这样了，为了对应更加方便，通常用的时候声明数组会多给出一个空间，从下标为1开始用，下标为0的不用，下面给出的方法也是从1开始。

 

//对a数组中的某一值进行加操作
void add(int k,int num)  
{  
    while(k<=n)  
    {  
        tree[k]+=num;  
        k+=k&-k;  
    }  
} 

//对某一值进行更改时
void change(int k,int num)  
{  
    int n=num-tree[k];//区别于对某值进行加操作，加操作是在原有基础上更改，而如果要直接对某值更新时要借用加操作
    while(k<=n)  //那么下面这段while可以改成add（n,num）;
    {  
        tree[k]+=num;  
        k+=k&-k;  
    }  
} 

int read(int k)//求1~k的区间和  
{  
    int sum=0;  
    while(k>0)  
    {  
        sum+=tree[k];  
        k-=k&-k;  //求区间和时会反向用加尾操作，即把c对应的a全部找出来
    }  
    return sum;  
}  

int sumIK(int i,int k)//i~k的区间和  
{  
    sum(i);
    sum(k+1);
    return sum(k+1)-sum(i);//借用前面的求和，但是要注意，实际上应该是k-（i-1），因为从1开始，所以两边都要加上1
}  

 

Solution:

public class NumArray {

    int[] btree;
    int[] arr;
    
    public NumArray(int[] nums) {
       btree = new int[nums.length+1];
        arr = nums;
 
        for(int i=0; i<nums.length; i++){
            add(i+1, nums[i]);
        }
        
    }
    
    void add(int i,int value){
        
        for(;i<btree.length;i+=i&(-i))
        {
            btree[i]+=value;
            
        }
    }
    
    void update(int i, int val) {
        add(i+1, val-arr[i]);
        arr[i]=val;
    }

    public int sumRange(int i, int j) {
        return sumHelp(j+1)-sumHelp(i);
    }
    public int sumHelp(int i){
        int sum=0;
        for(;i>=1;i-=i&(-i))
        {
            sum+=btree[i];
            
        }
        // while((boolean)i)
        // {
        //     sum+=btree[i];
        //     i-=i&(-i);
        // }
        return sum;
    }
}


// Your NumArray object will be instantiated and called as such:
// NumArray numArray = new NumArray(nums);
// numArray.sumRange(0, 1);
// numArray.update(1, 10);
// numArray.sumRange(1, 2);