平衡二叉树的时间复杂度为啥是对数

Posted 2023-05-05

它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。常用算法有红黑树、AVL、Treap、伸展树等。在平衡二叉搜索树中，我们可以看到，其高度一般都良好地维持在O（log2n），大大降低了操作的时间复杂度。 参考技术A

平衡二叉树（AVL）

那对图 1 进行下改造，把数据重新节点重新连接下，图 2 如下：

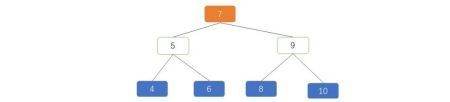
图 2 可以看到以下特性：

1. 所有左子树的节点都小于其对应的父节点（4，5，6）<（7）；（4）<（5）；（8）< （9）；

2. 所有右子树上的节点都大于其对应的父节点（8，9，10）>（7）；（6）>（5）；（10）>（9）；

3. 每个节点的平衡因子差值绝对值 <=1；

4. 每个节点都符合以上三个特征。

满足这样条件的树叫平衡二叉树（AVL）树。

问：那再次查找节点 5，需要遍历多少次呢？

由于数据是按照顺序组织的，那查找起来非常快，从上往下找：7-5，只需要在左子树上查找，也就是遍历 2 次就找到了 5。假设要找到叶子节点 10，只需要在右子树上查找，那也最多需要 3 次，7-9-10。也就说 AVL 树在查找方面性能很好，最坏的情况是找到一个节点需要消耗的次数也就是树的层数， 复杂度为 O(logN)

如果节点非常多呢？假设现在有 31 个节点，用 AVL 树表示如图 3：

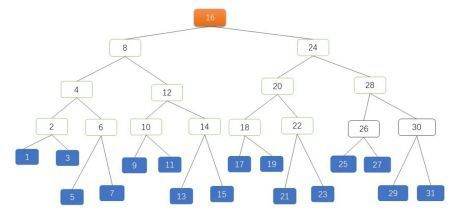
图 3 是一棵高度为 4 的 AVL 树，有 5 层共 31 个节点，橙色是 ROOT 节点，蓝色是叶子节点。对 AVL 树的查找来看起来已经很完美了，能不能再优化下？比如，能否把这个节点里存放的 KEY 增加？能否减少树的总层数？那减少纵深只能从横向来想办法，这时候可以考虑用多叉树。

数据结构-平衡二叉树

平衡二叉树的重点在于对不平衡的进行旋转从而使它达到平衡.

下面是我理解的平衡二叉树的操作总结:

平衡因子(BF)：
 这是一个描述平衡度的一个量,计算的方式为 左子树的深度-右子树的深度。

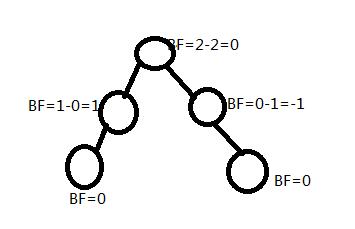
我们可以从BF中就能知道左子树和右子树之间的平衡程度。

插入数据

平衡二叉树最复杂的就是将数据插入到树中了，因为要涉及到位置的调整。对于位置的调整在平衡二叉树中成为树的旋转.根据平衡因子的状态分为左旋和右旋.

那什么时候需要进行旋转呢?

这个问题确实值得思考,一般都是在平衡因子的绝对值大于1的时候就需要进行旋转了，也就是说左右子树的深度相差超过了1.

那从什么地方做为跟节点进行旋转呢？

这里有一个术语叫做最小不平衡子树,就是平衡因子绝对值大于1,并且最接近叶子节点的。

我们旋转的时候,只需要对最小不平衡子树进行旋转就可以了。

左旋：

当平衡因子为正数的时候并且大于1的时候，进行左旋，左旋的方式为：
根节点的左子树的右子树作为根节点的右子树，根节点作为左子树的右子树。

 

 

 右旋：

当平衡因子为负数的时候,并且小于-1的时候进行右旋，右旋的方式为：
将根节点的右节点的左子树作为根节点的右子树.
根节点作为跟节点的右节点的左子树。

 

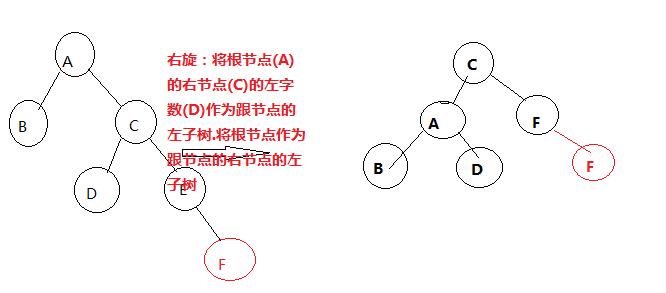
注意： 

上面两种实例根节点和子节点都是同一符号的,所以简单的进行左旋或者右旋就可以了。如下图：

,但是如果我们遇到符号不相同的情况下,需要进行两次旋转，如下图：

 

这种情况下，第一次旋转是将C作为根节点右旋,之后再进行左旋.

我们只需要记住正数的时候进行右旋,负数的时候进行左旋即可。

 上面的原理讲完了,下面是具体的JAVA代码实现：

package com.hotusm.datastructure.tree;

/**
 * @author luqibao
 * @date 2017/3/31
 */
public class AVLTree {


    /**
     * 平衡因子所属的状态
     */
    private static final int LH = 1;   //左边高
    private static final int EH = 0;   //一样高
    private static final int RH = -1;  //右边高


    private TreeNode root;  //树的根


    /**
     * 向平衡二叉树插入节点
     *
     * @param data
     */
    public void insertNode(int data) {

        if (this.root == null) {
            this.root = new TreeNode(null, null, EH, data, null);
            return;
        }
        insertAVLNode(this.root, data);

    }


    /**
     * 进行右旋
     *
     * @param treeNode 需要旋转的根
     */
    /*
     * 右旋
     * 将根的左子树的右子树作为根的左子树
     * 左子树的右子树指向根(最后左子树变为了根,根变为了右子树)
     */
    private void rRotate(TreeNode treeNode) {
        TreeNode root = treeNode.getLeft();
        if (treeNode == this.root) {
            this.root = root;
        }
        treeNode.setLeft(root.getRight());
        root.setRight(treeNode);
    }

    /**
     * 进行左旋
     *
     * @param treeNode 需要旋转的根
     */
    /*
    * 左旋
    * 将根的右子树的左子树作为根的右子树
    * 右子树的左子树指向根（最后右子树变为个根,根变为了左子树）
    * */
    private void lRotate(TreeNode treeNode) {
        TreeNode root = treeNode.getRight();
        if (treeNode == this.root) {
            this.root = root;
        }
        treeNode.setRight(root.getLeft());
        root.setLeft(treeNode);
    }

    /**
     * 左平衡旋转（左边平衡因子太大的原因  需要向右移动）
     *
     * @param root
     */
    private void leftBalance(TreeNode root) {
        TreeNode leftNode = root.getLeft();
        switch (leftNode.getBf()) {
            case LH:
                root.setBf(EH);
                leftNode.setBf(EH);
                rRotate(root);
                break;
            //如果是这种情况  根和左子树平衡因子不是同符号的  所以需要两次的旋转
            case RH:
                TreeNode doubleLeftNode = leftNode.getRight();// 左子树的右子树
                switch (doubleLeftNode.getBf()) {
                    case RH:
                        root.setBf(EH);
                        leftNode.setBf(LH);
                        break;
                    case EH:
                        root.setBf(EH);
                        leftNode.setBf(EH);
                        break;
                    case LH:
                        root.setBf(RH);
                        leftNode.setBf(EH);
                        break;
                }
                doubleLeftNode.setBf(EH);
                lRotate(leftNode);
                rRotate(root);
                break;
        }
    }

    /**
     * 右平衡旋转 右边平衡因子太大的原因
     *
     * @param root
     */
    private void rightBalance(TreeNode root) {

        TreeNode rightNode = root.getRight();

        switch (rightNode.getBf()) {
            case RH:
                root.setBf(EH);
                rightNode.setBf(EH);
                lRotate(root);
                break;
            case LH: //如果是这种情况 那么根和右子树的平衡因子不同符号 所以需要进行两次的旋转
                TreeNode doubleLeftNode = rightNode.getLeft();
                switch (doubleLeftNode.getBf()) {
                    case LH:
                        root.setBf(EH);
                        rightNode.setBf(RH);
                        break;
                    case EH:
                        root.setBf(EH);
                        rightNode.setBf(EH);
                        break;
                    case RH:
                        root.setBf(LH);
                        rightNode.setBf(EH);
                        break;
                }
                doubleLeftNode.setBf(EH);
                rRotate(rightNode);
                lRotate(root);
                break;
        }

    }

    /**
     * 向平衡二叉树插入数据data
     * 如果增高那么返回true  否则返回false
     *
     * @param data
     * @return
     */
    private boolean insertAVLNode(TreeNode root, int data) {
        boolean taller = false;
        if (root.getData() == data) {
            return false;
        }
        if (data < root.getData()) {
            if (root.getLeft()==null){
                TreeNode child=new TreeNode(null,null,EH,data,root);
                root.setLeft(child);
                if (root.getBf()==EH){
                    root.setBf(LH);
                    return true;
                }
                /*
                 * 在child 节点未插入到root的左子树中的时候
                 * root的BF只能有两种情况 EH(左右都没节点) 和 RH(有右叶子节点)
                 * 所以还有一种可能就是当时RH的时候 BF变为EH
                 * */
                root.setBf(EH);
            }else {
                taller=insertAVLNode(root.getLeft(),data);
                if (taller){
                    switch (root.getBf()){
                        case LH:
                            leftBalance(root);
                            taller=false;
                            break;
                        case EH:
                            /*
                             *进行上一级的回溯
                             *      O
                             *    O   O
                             *  O  O
                             */
                            root.setBf(LH);
                            taller=true;
                            break;
                        default:
                            root.setBf(EH);
                            taller=false;
                    }
                }
            }
        } else {
            if (root.getRight()==null){
                TreeNode child=new TreeNode(null,null,EH,data,root);
                root.setRight(child);
                if (root.getBf()==EH){
                    root.setBf(RH);
                }
                /*
                * 和上面的类似,在右子树插入到root之前 root的BF只有两种情况 EH（没有左右节点） LH （只有左叶子节点）
                * */
                root.setBf(EH);
            }else {
                taller=insertAVLNode(root.getRight(),data);
                if (taller){
                    switch (root.getBf()){
                        case RH:
                            rightBalance(root);
                            taller=false;
                            break;
                        case LH:
                            root.setBf(EH);
                            taller=false;
                            break;
                        default:
                        /*
                         *这里会进行回溯到更上的一级进行判断 从而进行旋转
                         *              O
                         *            O   O
                         *               O  O
                         */
                            root.setBf(RH);
                            taller=true;
                    }
                }
            }
        }
        return taller;
    }

    public static void main(String[] args) {
        testInsertAVLTree();
    }

    public static void testInsertAVLTree() {
        AVLTree avlTree = new AVLTree();
        avlTree.insertNode(1);
        avlTree.insertNode(2);
        avlTree.insertNode(3);
        avlTree.insertNode(4);
        avlTree.insertNode(5);

    }

    /**
     * 树的节点
     */
    public static class TreeNode {

        private TreeNode left;
        private TreeNode right;
        private TreeNode parent;
        private int bf; //平衡因子
        private int data;

        public TreeNode(TreeNode left, TreeNode right, int bf, int data, TreeNode parent) {
            this.left = left;
            this.right = right;
            this.bf = bf;
            this.data = data;
            this.parent = parent;
        }

        public TreeNode getLeft() {
            return left;
        }

        public void setLeft(TreeNode left) {
            this.left = left;
        }

        public TreeNode getRight() {
            return right;
        }

        public void setRight(TreeNode right) {
            this.right = right;
        }

        public int getBf() {
            return bf;
        }

        public void setBf(int bf) {
            this.bf = bf;
        }

        public int getData() {
            return data;
        }

        public TreeNode getParent() {
            return parent;
        }

        public void setParent(TreeNode parent) {
            this.parent = parent;
        }

        public void setData(int data) {
            this.data = data;
        }

        @Override
        public String toString() {
            return "TreeNode{" +
                    "left=" + left +
                    ", right=" + right +
                    ", bf=" + bf +
                    ", data=" + data +
                    \'}\';
        }
    }
}

代码中进行了详细的注释，看起来应该是没问题的。

参考：大话数据结构 第八章