LeetCode（45）： 跳跃游戏 II

Posted 2020-11-10 Ariel_一只猫的旅行

Hard！

题目描述：

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

你的目标是使用最少的跳跃次数到达数组的最后一个位置。

示例:

输入: [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
     从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

说明:

假设你总是可以到达数组的最后一个位置。

解题思路：

这题是之前那道Jump Game 跳跃游戏 的延伸，那题是问能不能到达最后一个数字，而此题只让我们求到达最后一个位置的最少跳跃数，貌似是默认一定能到达最后位置的? 此题的核心方法是利用贪婪算法Greedy的思想来解，想想为什么呢？ 为了较快的跳到末尾，我们想知道每一步能跳的范围，这里贪婪并不是要在能跳的范围中选跳力最远的那个位置，因为这样选下来不一定是最优解，这么一说感觉又有点不像贪婪算法了。我们这里贪的是一个能到达的最远范围，我们遍历当前跳跃能到的所有位置，然后根据该位置上的跳力来预测下一步能跳到的最远距离，贪出一个最远的范围，一旦当这个范围到达末尾时，当前所用的步数一定是最小步数。

我们需要两个变量cur和pre分别来保存当前的能到达的最远位置和之前能到达的最远位置，只要cur未达到最后一个位置则循环继续，pre先赋值为cur的值，表示上一次循环后能到达的最远位置，如果当前位置i小于等于pre，说明还是在上一跳能到达的范围内，我们根据当前位置加跳力来更新cur，更新cur的方法是比较当前的cur和i + A[i]之中的较大值，如果题目中未说明是否能到达末尾，我们还可以判断此时pre和cur是否相等，如果相等说明cur没有更新，即无法到达末尾位置，返回-1。

C++解法一：

 1 class Solution {
 2 public:
 3     int jump(vector<int>& nums) {
 4         int res = 0, n = nums.size(), i = 0, cur = 0;
 5         while (cur < n - 1) {
 6             ++res;
 7             int pre = cur;
 8             for (; i <= pre; ++i) {
 9                 cur = max(cur, i + nums[i]);
10             }
11             if (pre == cur) return -1; // May not need this
12         }
13         return res;
14     }
15 };

还有一种写法，跟上面那解法略有不同，但是本质的思想还是一样的，关于此解法的详细分析可参见http://www.cnblogs.com/lichen782/p/leetcode_Jump_Game_II.html。这里cur是当前能到达的最远位置，last是上一步能到达的最远位置，我们遍历数组，首先用i + nums[i]更新cur，这个在上面解法中讲过了，然后判断如果当前位置到达了last，即上一步能到达的最远位置，说明需要再跳一次了，我们将last赋值为cur，并且步数res自增1，这里我们小优化一下，判断如果cur到达末尾了，直接break掉即可。

C++解法二：

 1 class Solution {
 2 public:
 3     int jump(vector<int>& nums) {
 4         int res = 0, n = nums.size(), last = 0, cur = 0;
 5         for (int i = 0; i < n - 1; ++i) {
 6             cur = max(cur, i + nums[i]);
 7             if (i == last) {
 8                 last = cur;
 9                 ++res;
10                 if (cur >= n - 1) break;
11             }
12         }
13         return res;
14     }
15 };

要理解这个算法，首先明白，这个题只要我们求跳数，怎么跳，最后距离是多少，都没让求的。

大牛这个算法的思想主要是，扫描数组（废话。。。），以确定当前最远能覆盖的节点，放入curr。然后继续扫描，直到当前的路程超过了上一次算出的覆盖范围，那么更新覆盖范围，同时更新条数，因为我们是经过了多一跳才能继续前进的。

形象地说，这个是在争取每跳最远的greedy。举个栗子。

比如就是我们题目中的[2,3,1,1,4]。初始状态是这样的：cur表示最远能覆盖到的地方，用红色表示。last表示已经覆盖的地方，用箭头表示。它们都指在第一个元素上。

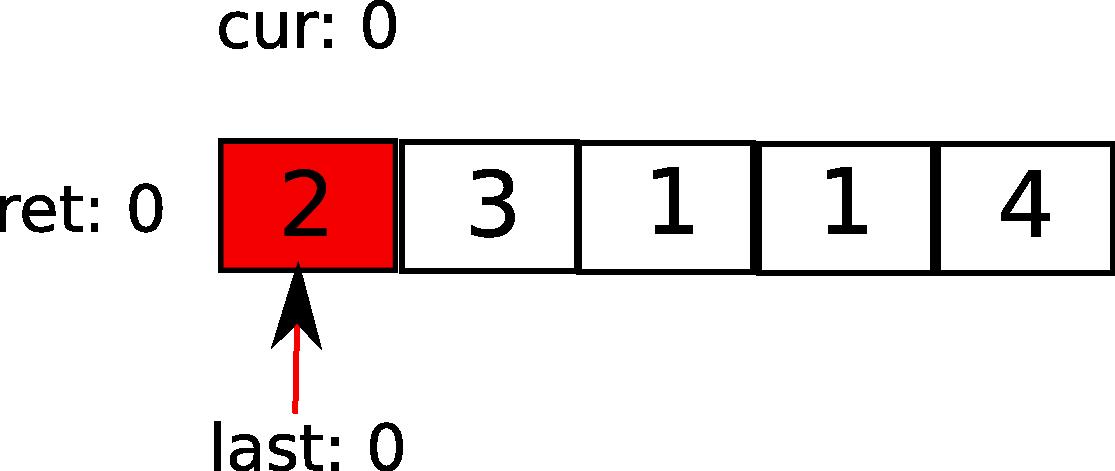
接下来，第一元素告诉cur，最远咱可以走2步。于是：

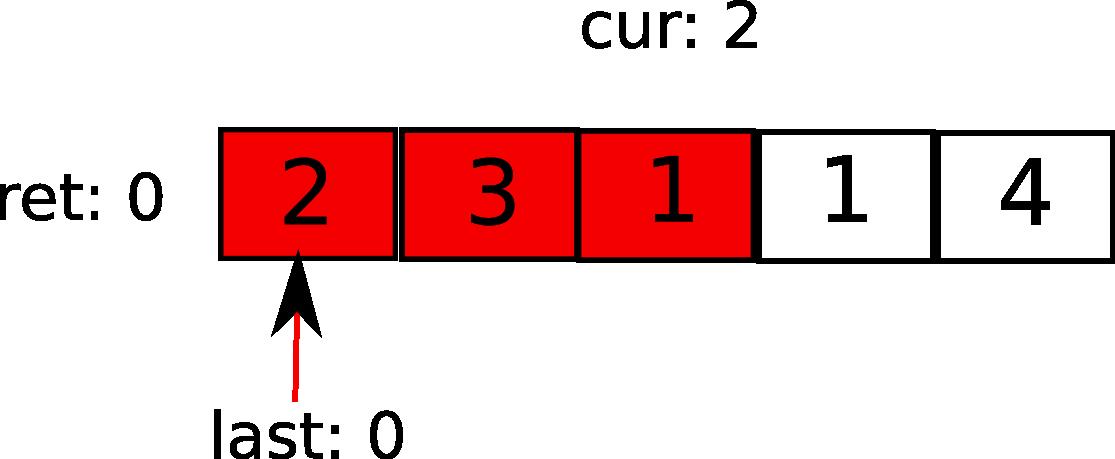
下一循环中，i指向1（图中的元素3），发现，哦，i小于last能到的范围，于是更新last（相当于说，进入了新的势力范围），步数ret加1.同时要更新cur。因为最远距离发现了。

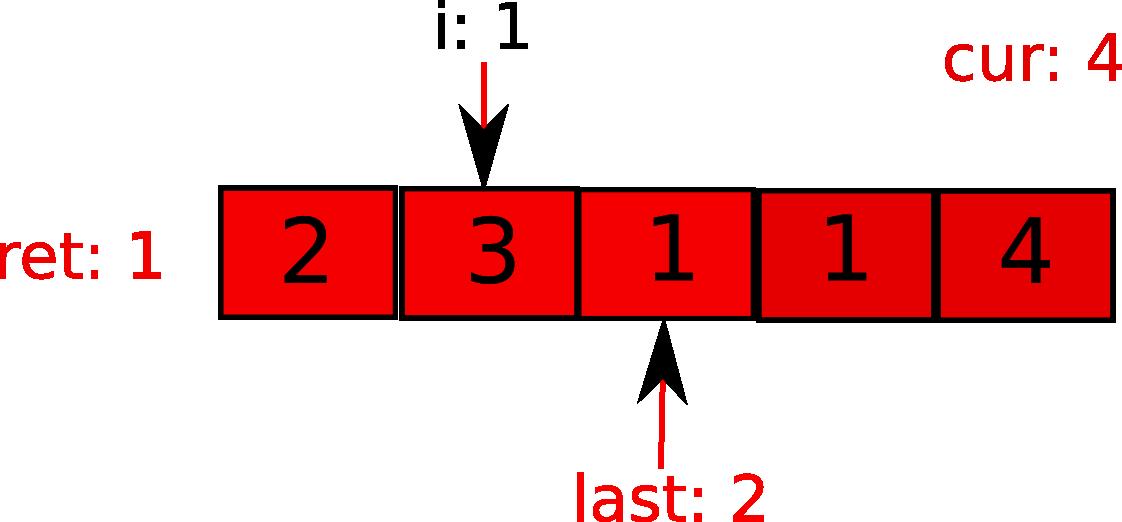
接下来，i继续前进，发现i在当前的势力范围内，无需更新last和步数ret。更新cur。

i继续前进，接下来发现超过当前势力范围，更新last和步数。cur已然最大了。

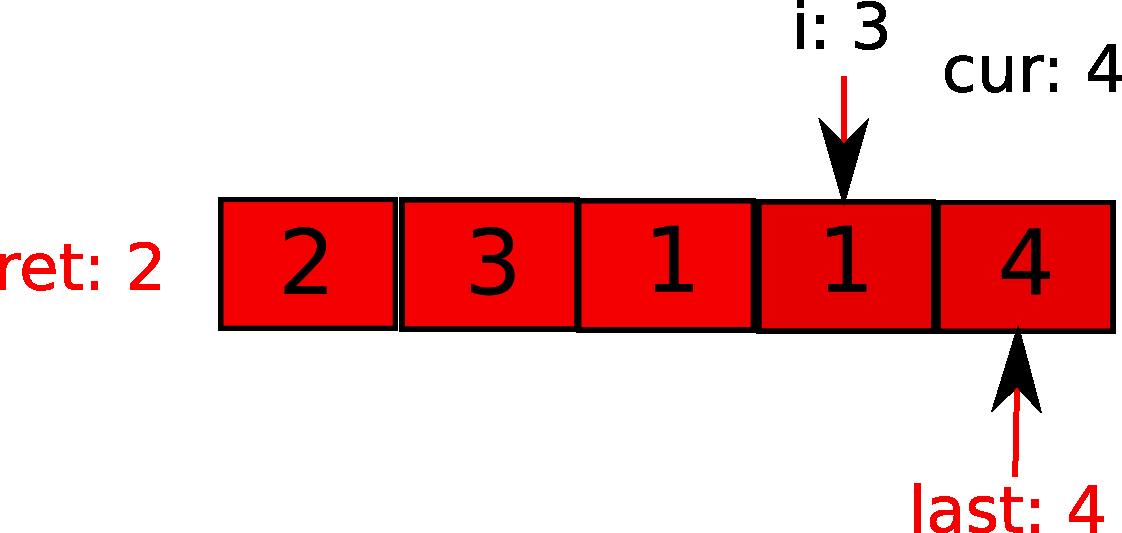
最后，i到最后一个元素。依然在势力范围内，遍历完成，返回ret。

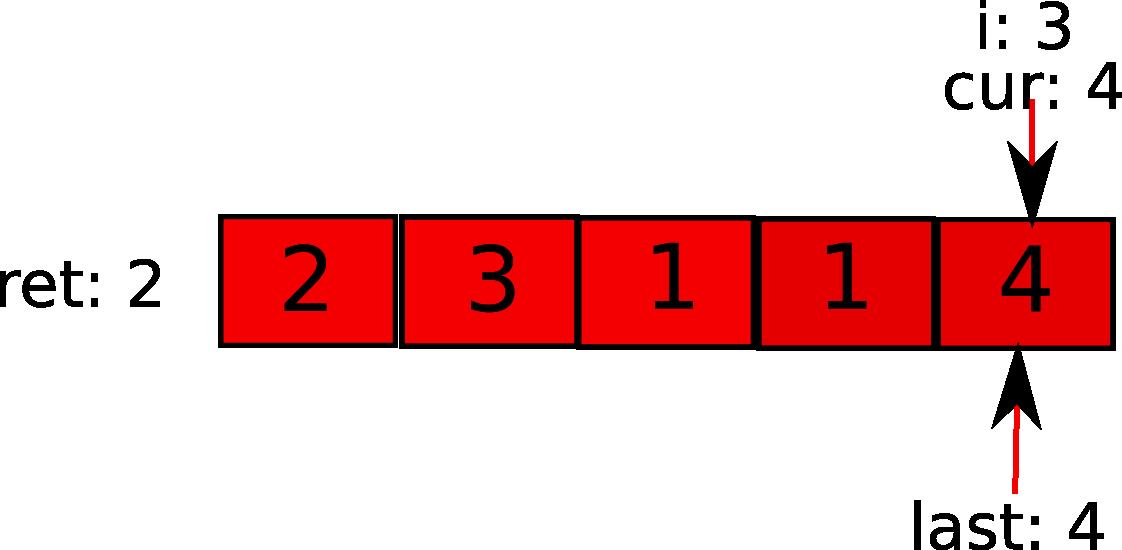
这道题让我们明白一个道理：

不要做无必要的计算。

对了，有同学会问，那为啥要用last，直接用curr跳不就行了。直接用curr跳那每次都是跳最远的，但是最优路径不不一定是这样。该算法时间复杂度为O(n)。

C++解法三：

 1 /*
 2  * We use "last" to keep track of the maximum distance that has been reached
 3  * by using the minimum steps "ret", whereas "curr" is the maximum distance
 4  * that can be reached by using "ret+1" steps. Thus,
 5  * curr = max(i+A[i]) where 0 <= i <= last.
 6  */
 7 class Solution {
 8 public:
 9     int jump(int A[], int n) {
10         int ret = 0;
11         int last = 0;
12         int curr = 0;
13         for (int i = 0; i < n; ++i) {
14             if (i > last) {
15                 last = curr;
16                 ++ret;
17             }
18             curr = max(curr, i+A[i]);
19         }
20 
21         return ret;
22     }
23 };