Chapter10.3：描述函数法

Posted 2023-04-05 FUXI_Willard

该系列博客主要讲述Matlab软件在自动控制方面的应用，如无自动控制理论基础，请先学习自动控制系列博文，该系列博客不再详细讲解自动控制理论知识。
自动控制理论基础相关链接：https://blog.csdn.net/qq_39032096/category_10287468.html?spm=1001.2014.3001.5482
博客参考书籍：《MATLAB/Simulink与控制系统仿真》。

---

---

3.描述函数法

3.1 描述函数的基本概念

3.1.1 描述函数的定义

设非线性环节输入输出描述为：
$$y=f(x)$$
当非线性环节的输入信号为正弦信号：
$$x(t)=A\sin \omega t$$
对非线性环节的稳态输出$y(t)$进行谐波分析；

一般情况下，$y(t)$为非正弦的周期信号，可以展开成傅里叶级数：
$$y(t)=A_0+\sum _{n=1}^{\infty }(A_n\cos n\omega t+B_n\sin n\omega t)=A_0+\sum _{n=1}^{\infty }{Y}_n\sin (n\omega t+{\phi }_n)$$
其中：$A_0$为直流分量；$Y_n\sin (n\omega t+{\phi }_n)$为第$n$次谐波分量，且有：
$$Y_n=\sqrt{A_n^2+B_n^2},{\phi }_n=\arctan \frac{A_n}{B_n}$$
其中：$A_n、B_n$为傅里叶系数；
$$A_n=\frac{1}{\pi }{\int }_0^{2\pi }y(t)\cos n\omega t\mathrm{d}(\omega t)，B_n=\frac{1}{\pi }{\int }_0^{2\pi }y(t)\sin n\omega t\mathrm{d}(\omega t)(n=1,2,\dots ,)$$
直流分量：
$$A_0=\frac{1}{2\pi }{\int }_0^{2\pi }y(t)\mathrm{d}(\omega t)$$
若$A_0=0$且当$n>1$时，$Y_n$均很小，则可近似认为非线性环节的正弦响应应仅有基波分量：
$$y(t)\approx A_1\cos \omega t+B_1\sin \omega t=Y_1\sin (\omega t+{\phi }_1)$$
定义正弦输入信号作用下，非线性环节的稳态输出中基波分量和输入信号的复数比为非线性环节的描述函数，用$N(A)$表示，即：
$$N(A)=|N(A)|{\mathrm{e}}^{j\angle N(A)}=\frac{Y_1}{A}{\mathrm{e}}^{j{\phi }_1}=\frac{B_1+\mathrm{j}{A}_1}{A}$$

3.1.2 非线性系统描述函数法分析的应用条件

1. 非线性系统应简化成一个非线性环节和一个线性部分闭环连接的典型结构图，如下图所示：

   

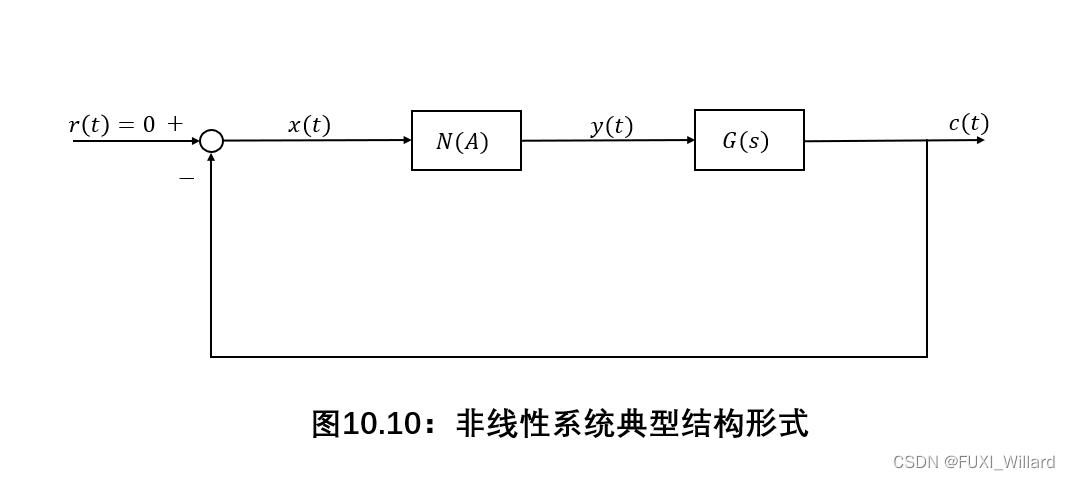
2. 非线性环节的输入输出特性$y(x)$应是$x$的奇函数，即$f(x)=-f(-x)$，或正弦输入下的输出为$t$的奇对称函数，即 y ( t

   数值计算方法 Chapter5. 解线性方程组的直接法

   • 数值计算方法 Chapter5. 解线性方程组的直接法
     • 0. 问题描述
     • 1. 消元法
       • 1. 三角方程组
         • 1. 对角方程组
         • 2. 下三角方程组
         • 3. 上三角方程组
       • 2. Gauss消元法
       • 3. Gauss-Jordan消元法
     • 2. 直接分解法
       • 1. Dolittle分解
       • 2. Courant分解
       • 3. 追赶法
       • 4. 对称正定矩阵的$LD{L}^T$分解

   0. 问题描述

   这一章节考察的就是如何求解线性方程组：

   $$\{\begin{array}{rl}{a}_{11}{x}_1+a_{12}{x}_2+...+a_{1n}{x}_n& =b_1\\ a_{21}{x}_1+a_{22}{x}_2+...+a_{2n}{x}_n& =b_2\\ ...& \\ a_{n1}{x}_1+a_{n2}{x}_2+...+a_{nn}{x}_n& =b_n\end{array}$$

   或者可以用矩阵来表达：

   $$\left(\begin{array}{cccc}{a}_{11}& a_{12}& ...& a_{1n}\\ a_{21}& a_{22}& ...& a_{2n}\\ ...& & & \\ a_{n1}& a_{n2}& ...& a_{nn}\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\\ ...\\ x_n\end{array}\right)=\left(\begin{array}{c}{b}_1\\ b_2\\ ...\\ b_n\end{array}\right)$$

   1. 消元法

   1. 三角方程组

   首先，我们来考察一些特殊形式的方程：

   1. 对角方程组

   对角方程组的函数形式如下：

   $$\left(\begin{array}{cccc}{a}_{11}& & & \\ & a_{22}& & \\ & & ...& \\ & & & a_{nn}\end{array}\right)以上是关于Chapter10.3：描述函数法的主要内容，如果未能解决你的问题，请参考以下文章$$

   matlab用最速下降法（梯度法）计算Rosenbrock函数，求程序代码

   NumPy 百分位函数不同于 MATLAB 的百分位函数

   求直接调用的matlab粒子群算法和模拟退火法的函数

   matlab用牛顿法计算潮流需要在命令窗口输入啥

   数值计算方法 Chapter5. 解线性方程组的直接法

   MATLAB遗传法