蓝桥杯之数论专题
Posted Selvaggia
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了蓝桥杯之数论专题相关的知识,希望对你有一定的参考价值。
蓝桥杯之数论专题
等差数列最短项数(最大公因子)
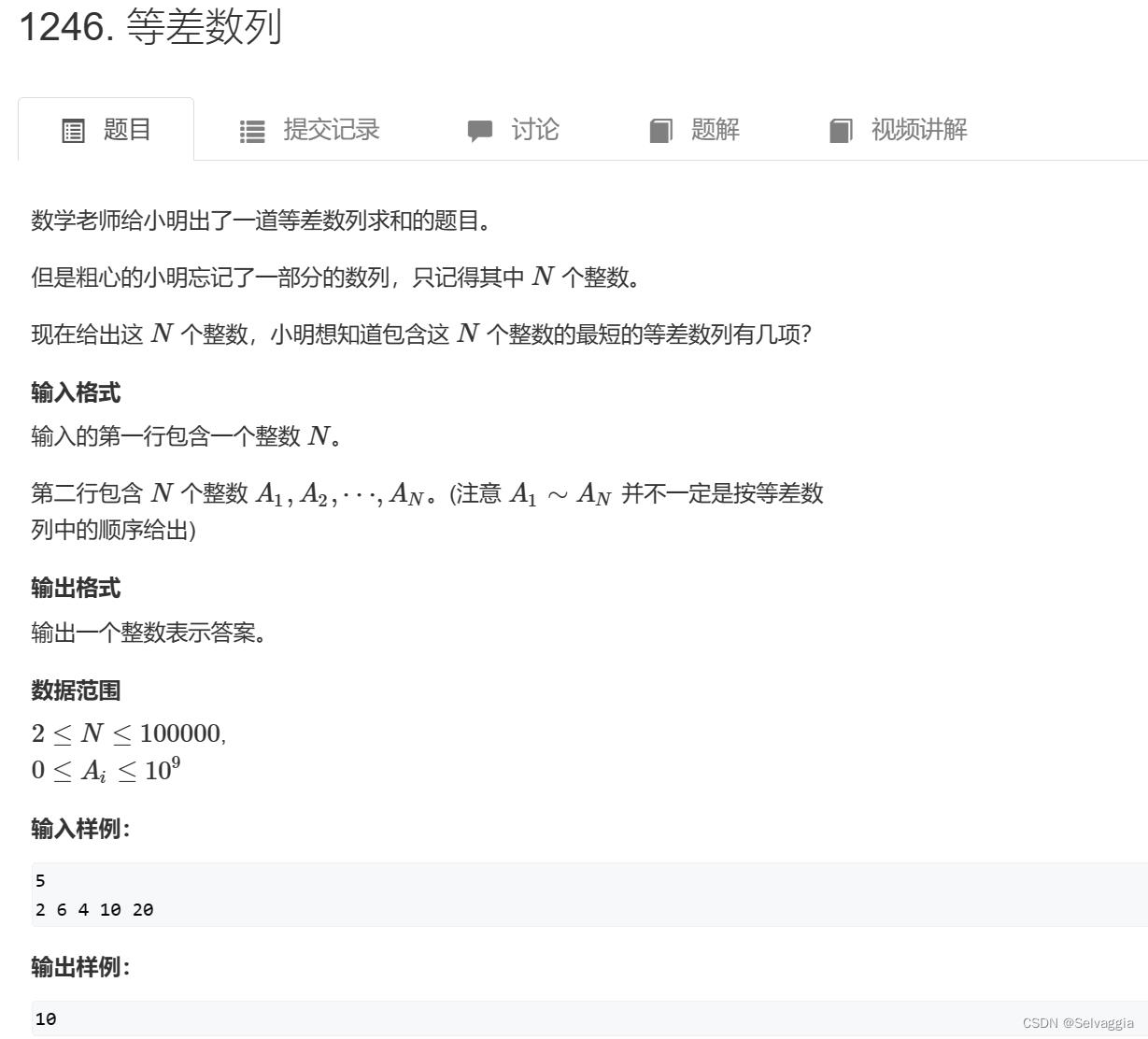

一开始简单以为是 n-1个差值里面的最小值,实际上不一定满足别的n-1个差值就恰好是该最小值的整数倍,应该找的是n-1个差值的最大公因数
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+5;
int n;
int a[N];
int gcd(int x,int y)//最大公因数 6 4 4 2 2 0
if(y)
return gcd(y,x%y);
else return x;
signed main()
cin>>n;
for(int i=0;i<n;i++)cin>>a[i];
sort(a,a+n);
// 等差要尽可能大,找到实际上最小的相差,不对,是要找差值的最大公因数
// int diff=0x3f3f3f3f;//等差数列最短则
// for(int i=0;i<n-1;i++)
// diff=min(diff,a[i+1]-a[i]);
//
int diff=0;
for(int i=0;i<n-1;i++)
diff=gcd(diff,a[i+1]-a[i]);
if(diff==0)cout<<n;//不要忘记特判这种特别的diff为0的等差数列
else
cout<<(a[n-1]-a[0])/diff+1;
return 0;
X的因子链(分解质因子)

输入样例:
2
3
4
10
100
输出样例:
1 1
1 1
2 1
2 2
4 6
思路:
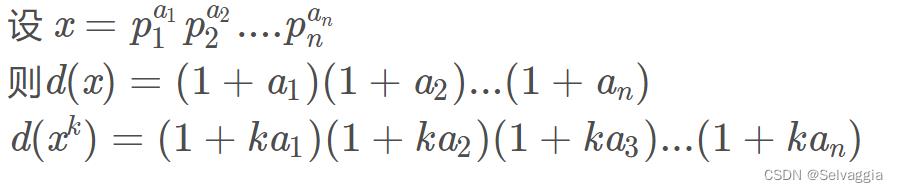
首先,X一定可以拆分成多个质数的乘积
构造最长序列,序列可以以一个质因数开头,每次乘以X的其中一个质因子,最后乘到X (因为质数是X因子中已经不可再分的了,把X拆分成质数的乘积后,可以保证序列的长度最长,序列的最长长度就是质因子的个数)
最大长度就是 总的质因子个数(幂次大于1的重复的质因子也计入)(将质因子逐项累乘的积)
素因子分解,得到结果后,可以看出最长的链,就是素因子依次乘过去,比如
100
−
>
2
,
2
,
5
,
5
100 − > 2 , 2 , 5 , 5
100−>2,2,5,5 ,那么最长链之一就是
2
,
4
,
20
,
100
2 , 4 , 20 , 100
2,4,20,100
求序列的数量:
如果质因子乘的次序不同,序列也会不同,因为质因子可能会有重复,
因此可以用排列组合的知识(多重集合的排列问题),
序列的个数=用质因子个数的阶乘除以各个质因子重复出现次数的阶乘
比如
2
∗
2
∗
2
∗
3
∗
3
∗
4
=
288
2 ∗ 2 ∗ 2 ∗ 3 ∗ 3 ∗ 4 = 288
2∗2∗2∗3∗3∗4=288 , 质因子数量总共是6, 2有三个,3有两个,4有1个,因此序列的最长长度为6,序列的数量= 6!/(3!*2!)
做法一:直接分解质因子
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+5;
int n,x;
int cnt=0;
// int prime[N];
int nums[N];
int sum=0;
void fun()
sum=0;
cnt=0;//质因子
memset(nums,0,sizeof(nums));
for(int i=2;i*i<=x;i++)
if(x%i==0)//哇趣,求余为0啊!!!
cnt++;
// prime[cnt]=i;
while(x%i==0)
x/=i;
nums[cnt]++;
sum+=nums[cnt];
if(x!=1)
cnt++;
// prime[cnt]=x;
nums[cnt]++;
sum+=nums[cnt];
signed main()//2^20等于1048576 1e6
while(cin>>x)
fun();//输出序列的最大长度就是总的质因子个数(将质因子逐项累乘的积)
cout<<sum<<" ";
// cnt!/ (nums[1]!*nums[2]!……)
int res=1;
// for(int i=1;i<=cnt;i++)
// res*=i;
// for(int j=1;j<=nums[i];j++)
// res/=j;
//
// //对于 cnt!/ (nums[1]!*nums[2]!……) 这种分子分母不确定的连乘数除法,
// 边乘边除不太合适,对于C(m,n)且(m>n)这种才合适,因为同时从1开始起步连乘
for(int i=1;i<=sum;i++)
res*=i;
for(int i=1;i<=cnt;i++)
for(int j=1;j<=nums[i];j++)
res/=j;
cout<<res;
cout<<endl;
return 0;
做法二:欧拉筛(原理是每一个非质数都被其最小质因数筛去,则可以记录合数的最小质因数,直接找到x的最小质因数,分解掉再继续找剩下部分的质因数)
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=(1<<20)+5;
int n,x;
int prime[N];
int vis[N];
int minPrime[N];
int nums[N];//非常注意多组输入,nums又是累加计数,一定要初始化
int sum=0;
void oula()
int cnt=0;
// memset(vis,0,sizeof(vis));
memset(prime,0,sizeof(prime));
memset(minPrime,0,sizeof(minPrime));
vis[0]=1;
vis[1]=1;
for(int i=2;i<=N;i++)
if(!prime[i])//prime数组代替vis
prime[cnt++]=i;
minPrime[i]=i;//质数i的最小质因数就是i本身
for(int j=0;j<cnt&&i*prime[j]<=N;j++)
prime[i*prime[j]]=1;prime数组代替vis
minPrime[i*prime[j]]=prime[j];
if(i%prime[j]==0)break;
// 向后筛出速度一定大于存储速度,当prime[cnt]是质数,一定早就经过了vis的检验
signed main()//2^20等于1048576 1e6
oula();
while(cin>>x)
int cnt=0;//x分解出来的质因子
sum=0;
while(x>1)
int mp=minPrime[x];
cnt++;
nums[cnt]=0;//初始化!!!
while(x%mp==0)
x/=mp;
sum++;
nums[cnt]++;
int res=1;
for(int i=1;i<=sum;i++)
res*=i;
for(int i=1;i<=cnt;i++)
for(int j=1;j<=nums[i];j++)
res/=j;
cout<<sum<<" "<<res;
cout<<endl;
return 0;
边乘边除的适宜情况
// for(int i=1;i<=cnt;i++)
// res*=i;
// for(int j=1;j<=nums[i];j++)
// res/=j;
//
// //对于 cnt!/ (nums[1]!*nums[2]!……) 这种分子分母不确定的连乘数除法,
// 边乘边除不太合适,对于C(m,n)且(m>n)这种才合适,因为同时从1开始起步连乘
int C(int a,int b)//C(5,2)=5*4/2/1
int res=1;
for(int i=a,j=1;j<=b;j++,i--)
res=res*i/j;//边乘边除
if(res>n)return res;//防止爆long long,反正大于n也不可能取这个值
return res;
聪明的燕姿

输入样例:
42
输出样例:
3
20 26 41
五指山(扩欧)

输入样例:
2
3 2 0 2
3 2 0 1
输出样例:
1
2
扩展欧几里得算法
欧几里得算法:可以求出两个数的最大公约数d 即(a, b) = d.
裴蜀定理 ------- 扩展欧几里得算法
可以求出最大公约数d,且可以求出 ax + by = d 的系数
首先我们已经知道了,如何通过扩展欧几里德算法,求出方程的其中一组解了
那么就可以继续往下看
给出两个方程
ax1+by1=gcd(a,b)
ax2+by2=gcd(a,b)
所以可以推出
ax1+by1=ax2+by2
a(x1-x2)=b(y2-y1)
然后我们知道gcd(a,b)为a,b的最大公因数,所以我们将 A=a/gcd(a,b),B=b/gcd(a,b),接着往下推出
A(x1-x2)=B(y2-y1)
现在A和B两个已经是互素了,所以又可以接着推出
(这个地方要好好理解,重点!)
A*(nB)=B(n*A)
(x1-x2)=n*B
(y2-y1)=n*A
这里我们从x入手
(x1-x2)=n*B
x1=x2+n*B
由此,我们推出了x解的通解公式 x=x0+n*B
同理,我们推出了y解的通解公式 y=y0-m*A
那么我们如果要求 x 的最小整数解,也就是 x0, 就是 x0=x%B
如果我们要求的是 ax+by=c,还得先转化 x=x*c/gcd(a,b).
然后套入我们的公式
B=b/gcd(a,b)
x0=x%(b/gcd(a,b))
证明来自这位博主
假设有整数k,p,q
n d x y
最先想到的是 (y-x+n)/d 能否得到一个整数,很显然整除要通过求余来体现
(y-x+n)%d==0,马上反应过来,可以不止多翻一圈来达到目的地,于是(y-x+k*n)%d==0
(2+3)%5,那么2%5==-3%5
//此时要是有同余方程的概念或者是 取模的规则(a+b)%mod=a%mod+b%mod
//于是有 (y-x)%d==(-k*n)%d,至于y-x+k*n 三项为什么是y-x在一边,因为这是个确定的数
//于是 k*n = x-y (mod d),再转换等式形式,k*n+p*d=x-y
//根据拓展欧几里得定理,首先x*a+y*p=gcd(a,p),如果x-y % gcd(a,p)!=0,那么impossible
//是可以求出满足的最小 k,p的,我们要求的就是最小的p
正负号问题
不对,首先是y-x+k*n=p*d, p*d-k*n=y-x,d的系数p一定要为正数但k可以随意
要保证d的系数p为正数,(y-x)%d==(-k*n)%d不可以这样继续,这样继续默认的是d的系数取任意整数值
应该是p*d+k*n=y-x
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+5;
int n,d,x,y,T;
int exgcd(int a,int p,int &x,int &y)//x*a+y*p=gcd(a,p)
if(!p)
x=1,y=0;
return a;//返回值是 gcd(a,p)
int res=exgcd(p,a%p,y,x);//参数要紧跟着呀!!
y-=a/p*x;
return res;
signed main()
cin>>T;
while(T--)
cin>>n>>d>>x>>y;
// p*d+k*n=x-y
int p,k;//求p
int res=exgcd(d,n,p,k);
if((y-x)%res!=0)cout<<"Impossible";
else
int t=(y-x)/res;
p*=t;
n/=res;
cout<<(p%n+n)%n;
if(T)cout<<endl;
return 0;
// 5
// 86 9 52 39
// 58 8 40 25
// 98 75 14 46
// 16 12 7 5
// 13 7 1 3
C循环(扩欧)
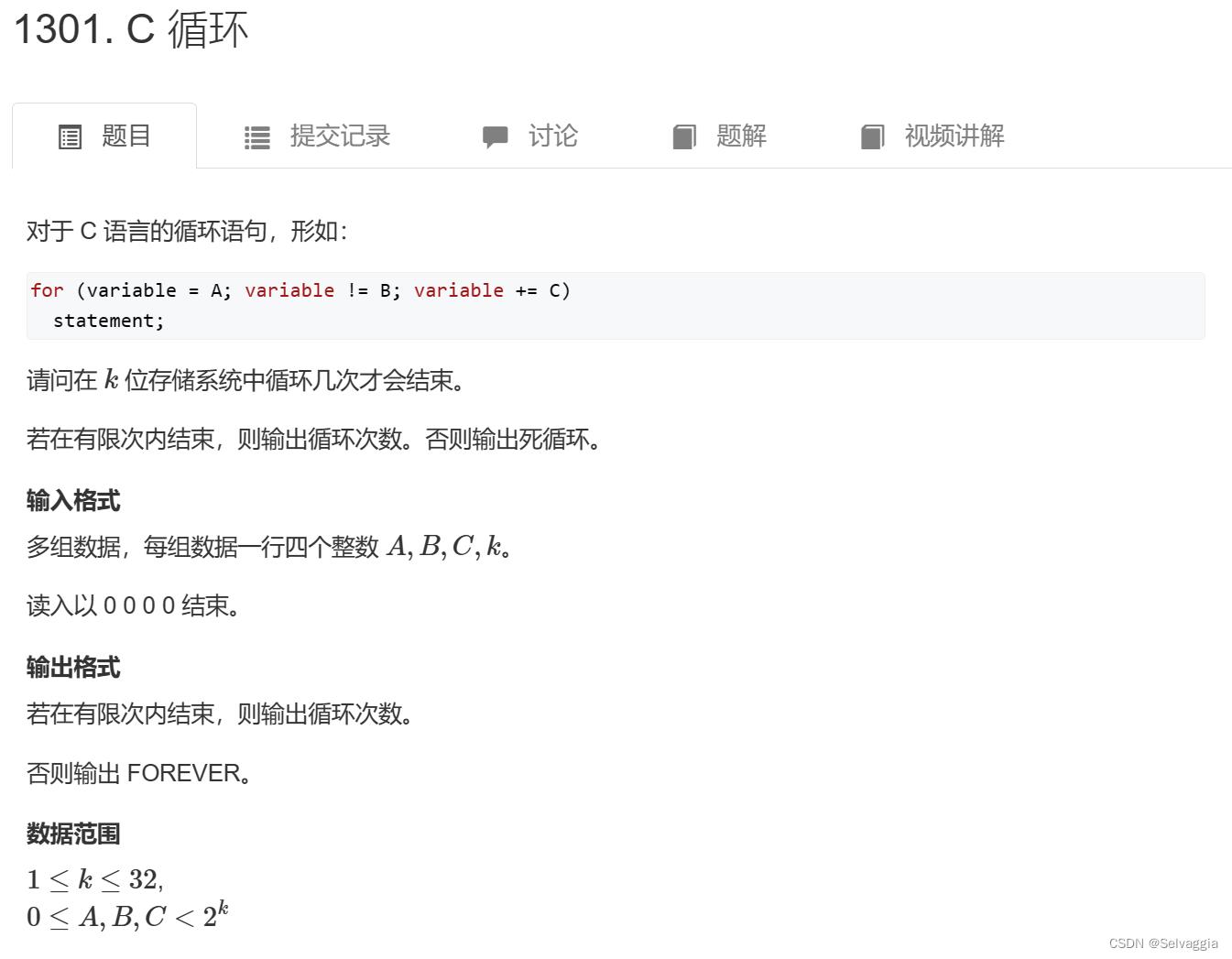
输入样例:
3 3 2 16
3 7 2 16
7 3 2 16
3 4 2 16
0 0 0 0
输出样例:
0
2
32766
FOREVER
A+p*C=B (mod k)
p*C+q*k=B-A,求p
用到拓展欧几里得算法的题本质上都是一个loop,不需要自己去对式子进行等价变换处理,对正负号处理可能会出错,比如上一题五指山,其实按题意可以直接抽象 (一圈是n,跳跃间隔是d,起点x,终点y,其实就是
x+p*d=y (mod n)
p*d+q*n=y-x,求p
#include <bits/stdc++.h>
using namespace std;
#define int long long int
int exgcd(int a,int p,int &x,int &y)//ax+py=gcd(a,p)
if(!p)
x=1,y=0;
return a;
int res=exgcd(p,a%p,y,x);
y-=a/p*x;
return res;
// A+p*C=B (mod k)
// p*C+q*k=B-A,求p
signed main()
int A,B,C,k,p,q;
while(cin>>A>>B>>C>>k)
if(!A&&!B&&!C&&!k)
return 0;
int K=1ll<<k;
int res=exgcd(C,K,p,q);
if((B-A)%res)cout<<"FOREVER";
else
p*=((B-A)/res);
K/=res;
// printf("%lld",(p%K+K)%K);
cout<<(p%K+K)%K;
cout<<endl;
return 0;
最大比例

输入样例1:
3
1250 200 32
输出样例1:
25/4
输入样例2:
4
3125 32 32 200
输出样例2:
5/2
输入样例3:
3
549755813888 524288 2
输出样例3:
4/1
正则问题
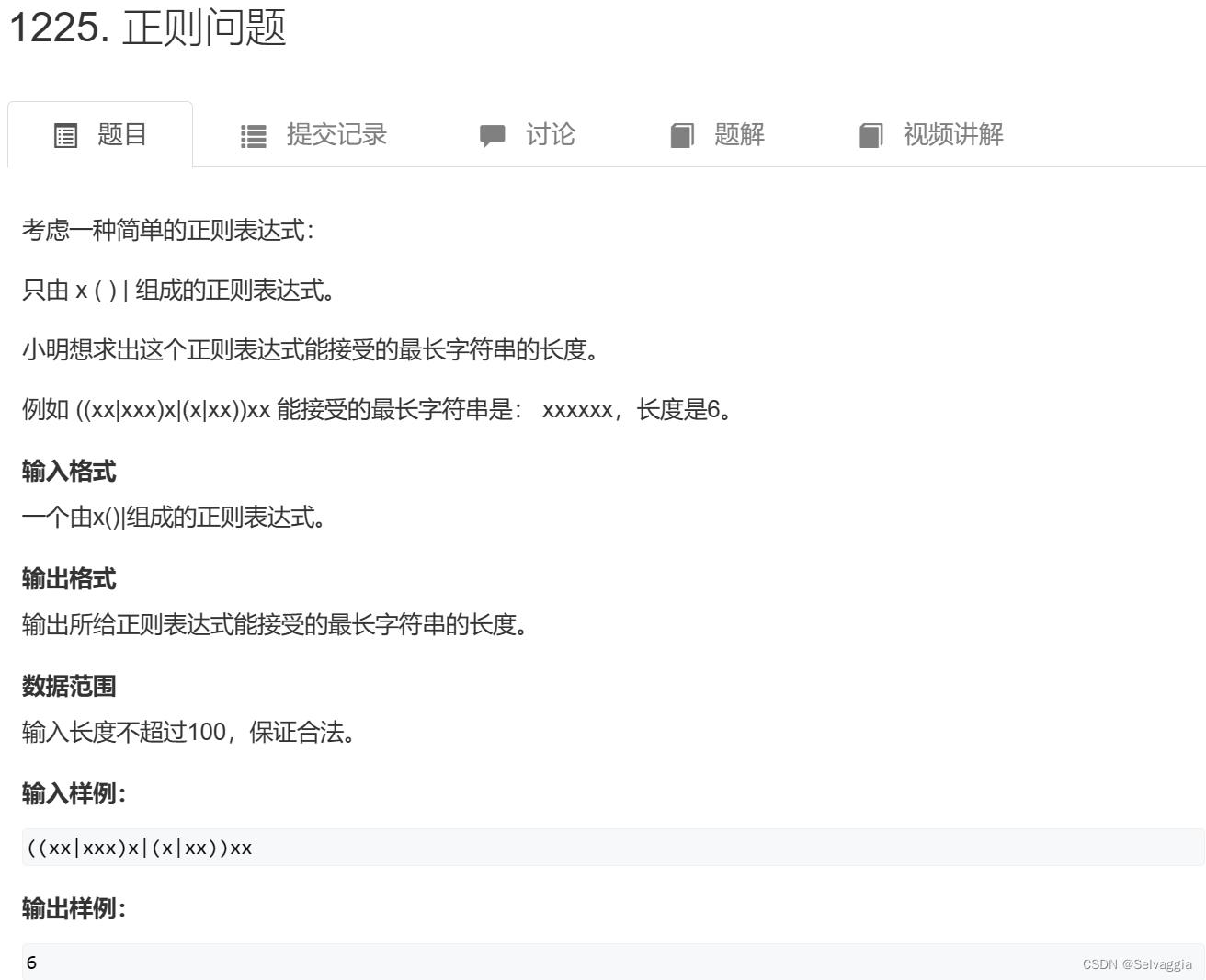
输入样例:
((xx|xxx)x|(x|xx))xx
输出样例:
6
蓝桥杯之算法模板题 Python版
蓝桥杯之算法模板题 Python版
文章目录
记录一下算法模板题,这样方便查阅和学习,希望好好加油
线段树
import os
import sys
N,Q = map(int,input().split())
arr = [0]
arr.extend(list(map(int,input().split())))
def ls(p):return p<<1 # p//2
def rs(p):return p<<1|1 # p//2 + 1
tree = [0 for _ in range(N<<2)] # 一共有2n个节点
tag = [0 for _ in range(N<<2)] # lazy_tag标记
def pushdown(p,pl,pr):
if tag[p]!=0:
mid = pl + pr >> 1
addtag(ls(p),pl,mid,tag[p])
addtag(rs(p),mid+1,pr,tag[p])
tag[p] = 0
# tree[p] = tree[lr(p)] + tree[rs(p)]
def push_up(p):
tree[p] = tree[ls(p)] + tree[rs(p)]
# 搭建线段树 节点的值是求和
def bulid(p,pl,pr):
if pl == pr:
# tree[p] = float('-inf')
tree[p] = arr[pl]
return
mid = pl + pr>>1
bulid(ls(p),pl,mid)
bulid(rs(p),mid+1,pr)
# tree[p] = tree[pl] + tree[pr]
push_up(p)
# 增加lazy_tag标记
def addtag(p,pl,pr,d):
tag[p] += d
tree[p] += d*(pr-pl+1)
def query(p,pl,pr,L,R): # L,R是查询区间
# 当前节点在查询区间内
if L <= pl and pr <= R: return tree[p]
pushdown(p,pl,pr) # 标记向下传递
res = 0
mid = pl + pr >>1
if L <= mid:
res+=query(ls(p),pl,mid,L,R)
if R > mid:
res+=query(rs(p),mid+1,pr,L,R)
return res
# 更新线段树,也就是加上k L,R是更新区间
def update(p,pl,pr,L,R,d):
if L<=pl and pr<=R:
addtag(p,pl,pr,d)
return
pushdown(p,pl,pr) # 标记向下传递
mid = pl + pr >> 1
if L <= mid: update(ls(p),pl,mid,L,R,d)
if R > mid: update(rs(p),mid+1,pr,L,R,d)
push_up(p)
bulid(1,1,N)
for _ in range(Q):
q = list(map(int,input().split()))
if q[0] == 1:
update(1,1,N,q[1],q[2],q[3])
elif q[0] == 2:
print(query(1,1,N,q[1],q[2]))
import os
import sys
def ls(p):return p<<1
def rs(p):return p<<1|1
def push_up(p):tree[p]=tree[rs(p)]+tree[ls(p)]
def build(p,pl,pr):
if pl==pr:
tree[p]=1
return
mid=(pl+pr)>>1
build(ls(p),pl,mid)
build(rs(p),mid+1,pr)
push_up(p)
def addtag(p,pl,pr,d):
tag[p]=d
tree[p]=d*(pr-pl+1)
def push_down(p,pl,pr):
if ~tag[p]!=0:
mid=(pl+pr)>>1
addtag(ls(p),pl,mid,tag[p])
addtag(rs(p),mid+1,pr,tag[p])
tag[p]=-1
# 把1变成0
def update0(p,pl,pr,cnt):
if cnt==0:return
if tree[p]==cnt:
addtag(p,pl,pr,0)
return
mid=(pl+pr)>>1
push_down(p,pl,pr)
if tree[ls(p)]>cnt:update0(ls(p),pl,mid,cnt)
else:
cnt-=tree[ls(p)]
addtag(ls(p),pl,mid,0)
update0(rs(p),mid+1,pr,cnt)
push_up(p)
# 把0变成1
def update1(p,pl,pr,cnt):
if cnt==0:return
if pr-pl+1-tree[p]==cnt:
addtag(p,pl,pr,1)
return
mid=(pl+pr)>>1
push_down(p,pl,pr)
if mid-pl+1-tree[ls(p)]>cnt:update1(ls(p),pl,mid,cnt)
else:
cnt-=(mid-pl+1-tree[ls(p)])
addtag(ls(p),pl,mid,1)
update1(rs(p),mid+1,pr,cnt)
push_up(p)
def query(p,pl,pr,L,R):
if L<=pl and pr<=R:return tree[p]
push_down(p,pl,pr)
mid=(pl+pr)>>1
res=0
if L<=mid:res+=query(ls(p),pl,mid,L,R)
if R>mid:res+=query(rs(p),mid+1,pr,L,R)
return res
n,m=map(int,input().split())
tree=[0 for _ in range(n<<2)]
tag=[-1 for _ in range(n<<2)]
build(1,1,n)
for _ in range(m):
op,num=map(int,input().split())
if op==0:
pos=n-tree[1]
cnt=max(0,num-pos)
update0(1,1,n,cnt)
elif op==1:
pos=tree[1]
cnt=max(0,n-num+1-pos)
update1(1,1,n,cnt)
ans1,ans2=[],[]
for i in range(1,n+1):
if query(1,1,n,i,i)==0:ans1.append(i)
else:ans2.append(i)
for x in ans1[::-1]+ans2:
print(x,end=' ')
DP 动态规划
dp, LIS **
'''
https://www.lanqiao.cn/problems/1188/learning/
难度: 中等 标签: dp, LIS
'''
import os
import sys
import bisect
# 请在此输入您的代码
n = int(input())
a = list(map(int,input().split()))
dp = [float('inf')]*(n+1)
dp[0] = a[0]
for i in range(1,n):
t = bisect.bisect_left(dp,a[i])
dp[t] = a[i]
print(bisect.bisect_left(dp,float('inf')))
01背包
动态转移方程
f
[
i
]
[
j
]
=
m
a
x
(
f
[
i
−
1
]
[
j
]
,
f
[
i
−
1
]
[
j
−
v
]
+
w
)
(
j
>
v
)
f[i][j] = max(f[i-1][j], f[i-1][j-v] + w)(j>v)
f[i][j]=max(f[i−1][j],f[i−1][j−v]+w)(j>v)
# https://www.lanqiao.cn/problems/1174/learning/
# 难度: 简单 标签: dp, 背包, 01背包
import os
import sys
# 请在此输入您的代码
N,V = map(int,input().split())
# f[N][V]
# f[i][j] 代表 i 件物品 , 容量为 j 的时候,得到最大的价值
f = [[0]*(V+1) for _ in range(N+1)]
for i in range(1,N+1):
# v为体积, w为价值
v, w = map(int, input().split())
for j in range(1,V+1):
# 第i件物品有两种选择,
# 第1种是选第i件物品,f[i-1][j]
# 第2种是不选第i件物品,f[i-1][j]
if j < v:
f[i][j] = f[i-1][j]
else:
f[i][j] = max(f[i-1][j], f[i-1][j-v] + w)
print(f[N][V])
完全背包
一般就是
f
[
i
]
[
j
]
=
m
a
x
(
f
[
i
−
1
]
[
j
−
k
∗
v
]
+
w
∗
k
)
(
0
<
=
k
<
j
/
/
v
)
f[i][j] = max(f[i-1][j-k*v] + w*k)(0<=k<j//v)
f[i][j]=max(f[i−1][j−k∗v]+w∗k)(0<=k<j//v)
不过可以转化为动态转移方程
f
[
i
]
[
j
]
=
m
a
x
(
f
[
i
−
1
]
[
j
]
,
f
[
i
]
[
j
−
v
]
+
w
)
f[i][j] = max(f[i-1][j],f[i][j-v] + w)
f[i][j]=max(f[i−1][j],f[i][j−v]+w)
'''
https://www.lanqiao.cn/problems/1175/learning/
难度: 简单 标签: DP, 背包, 完全背包
'''
import os
import sys
# 请在此输入您的代码
N,V = map(int,input().split())
# f[i][j]表示前i种,总体积不超过j,最大的总价值
f = [[0]*(V+1) for _ in range(N+1)]
# 完全背包问题,可以买多个
for i in range(1,N+1):
v,w = map(int,input().split以上是关于蓝桥杯之数论专题的主要内容,如果未能解决你的问题,请参考以下文章