RRT与RRT*算法具体步骤与程序详解(python)
Posted 问题很多de流星
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了RRT与RRT*算法具体步骤与程序详解(python)相关的知识,希望对你有一定的参考价值。
提示:前面写了A*、Dijkstra算法
文章目录
前言
RRT和RRT*的区别:
RRT的中文名为快速随机探索树,它的原理很简单,实际上就是维护一棵路径树:从起点开始,在空间中随机采样,并找到路径树上与采样点最接近且能与它无障碍地连接的点,连接这个点与采样点,将采样点加入路径树,直至终点附近区域被探索到。这种方式无法保证得到的路径是最优的。
RRT* 在RRT基础上做了改进,主要是进行了重新选择父节点和重布线的操作。试想在RRT中,我们的采样点最终与整棵树上和它最近的点连了起来,但这未必是最好的选择,我们的最终目的是让这个点与起点的距离尽可能近。RRT* 便对此做了改进,它在采样点加入路径树以后,以其为圆心画了一个小圈,考虑是否有更好的父节点,连到那些节点上能使起点到该点的距离更短(尽管那些节点并不是离采样点最近的点)。如果选择了更加合适的父节点,那么就把它们连接起来,并去除原来的连线(重布线)。
一、RRT的原理与步骤
我的原理启蒙:RRT算法原理图解
根据这篇文章,班门弄斧自己推导一遍这个过程,加强理解:

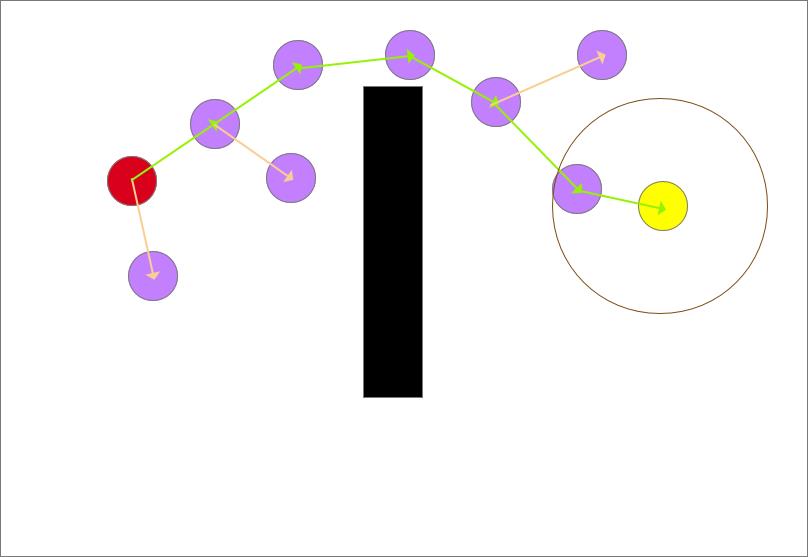
如图所示,红色的圆是起点,黄色的圆是终点,黑色代表障碍物
RRT的原理如下:
- 在空间中随机采样
如图中的蓝色圆,将其作为目标点

- 确定生长树的生长方向
以刚刚生成的随机点为目标,遍历生长树上的现存节点,计算每个节点到该随机点的距离,筛选出距离最小的节点作为最近点。此时树上仅存在起点(一颗没发芽的种子),所以直接选取起点为最近点。以最近点和随机点的连线为生长方向,如图中红色箭头所示
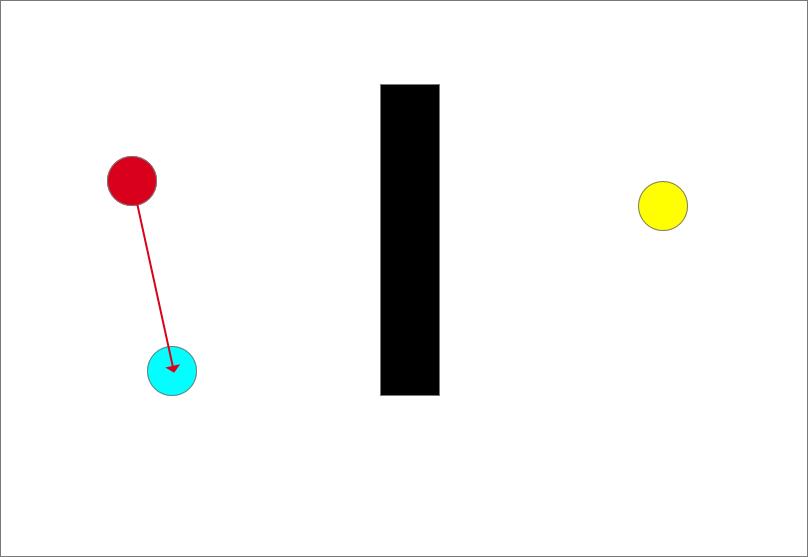
- 向目标点生长
生长步长是固定的,可由程序决定,但不宜太大也不宜太小,太小的话路径规划时间长,太大则会略过目标点。从此时的最近点也就是起点沿着生长方向生长一个步长得到一个生长点(紫色圆)
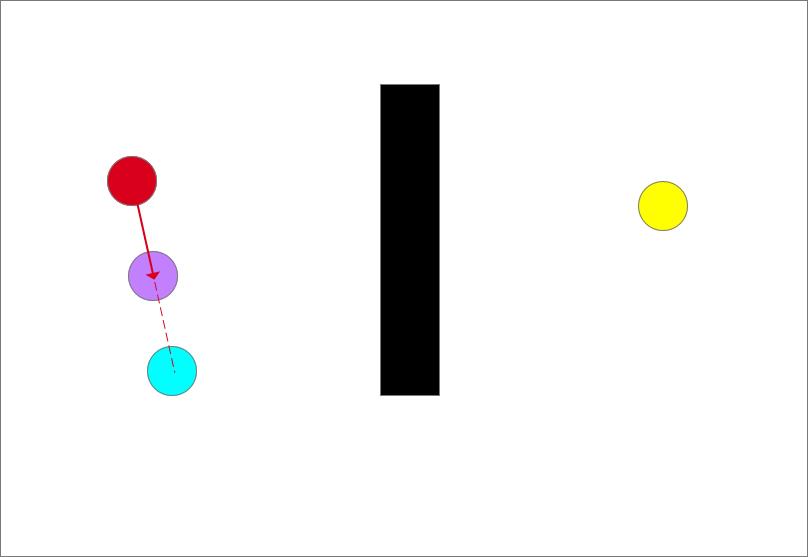
- 循环1~2步
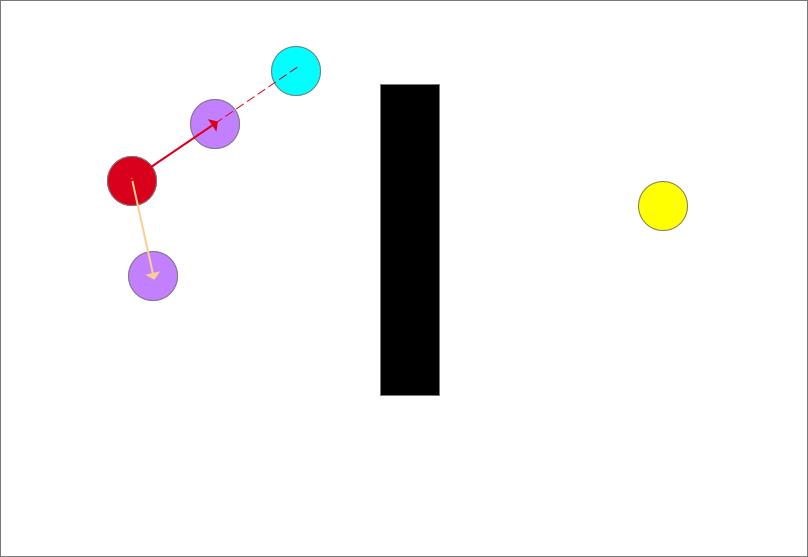
随机采样(蓝色圆形)
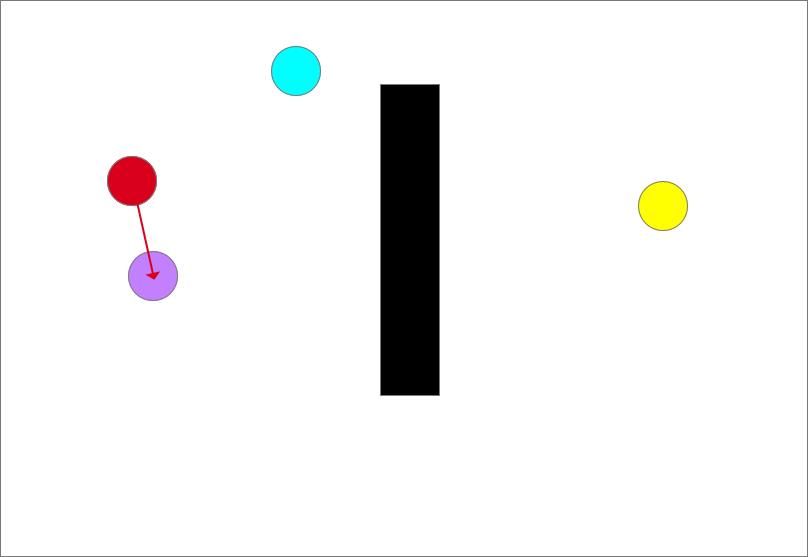
确定生长树的生长方向,图中共有两个点,红色和紫色圆,离目标点(蓝色)最近的是红色点,以最近点和随机点的连线为生长方向,如图中红色箭头所示
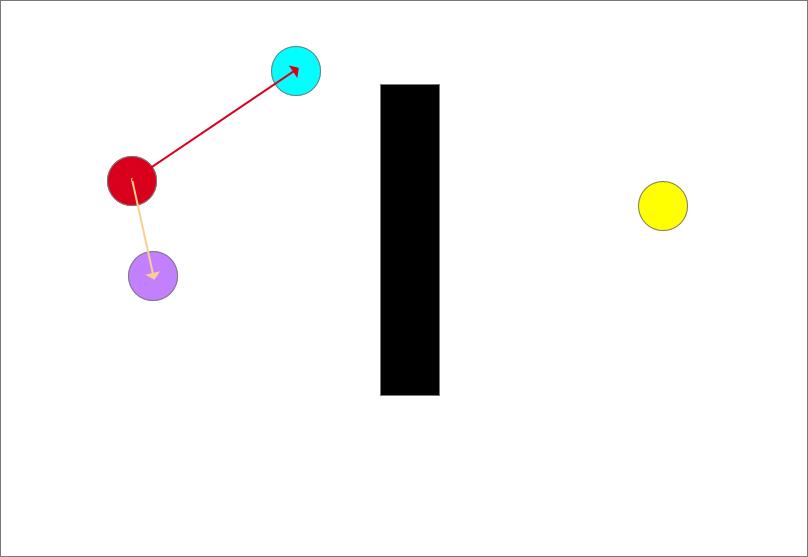
从此时的最近点也就是起点沿着生长方向生长一个步长得到一个生长点(紫色圆)
随机采样(蓝色圆形)
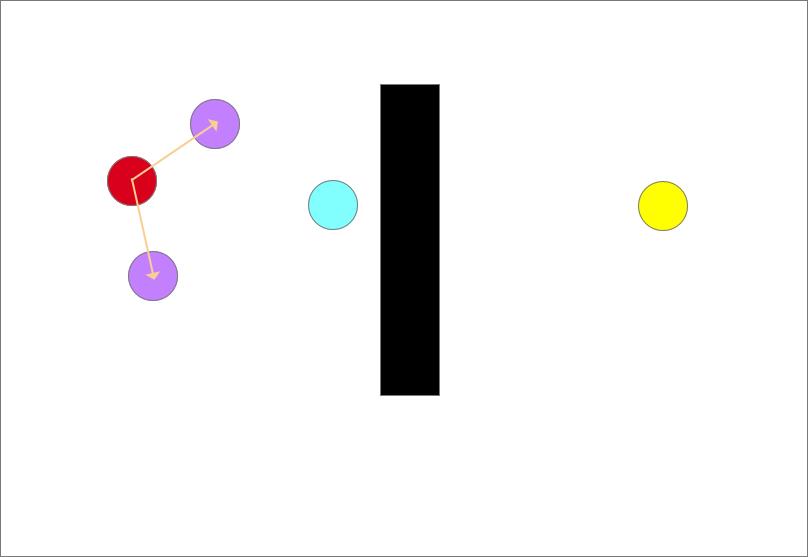
确定生长树的生长方向,以图中离目标点(蓝色)最近的点和随机点的连线为生长方向,如图中红色箭头所示,从此时的最近点也就是起点沿着生长方向生长一个步长得到一个生长点(紫色圆)
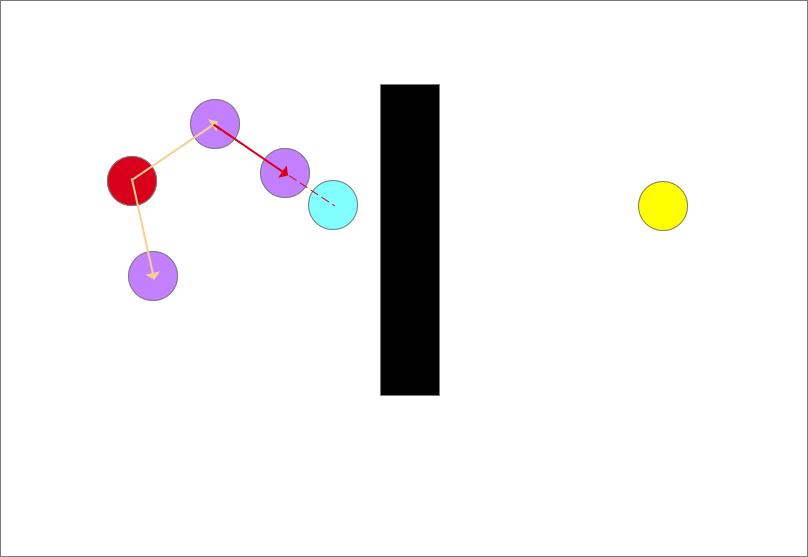
随机采样(蓝色圆形)
确定生长树的生长方向,以图中离目标点(蓝色)最近的点和随机点的连线为生长方向,如图中红色箭头所示
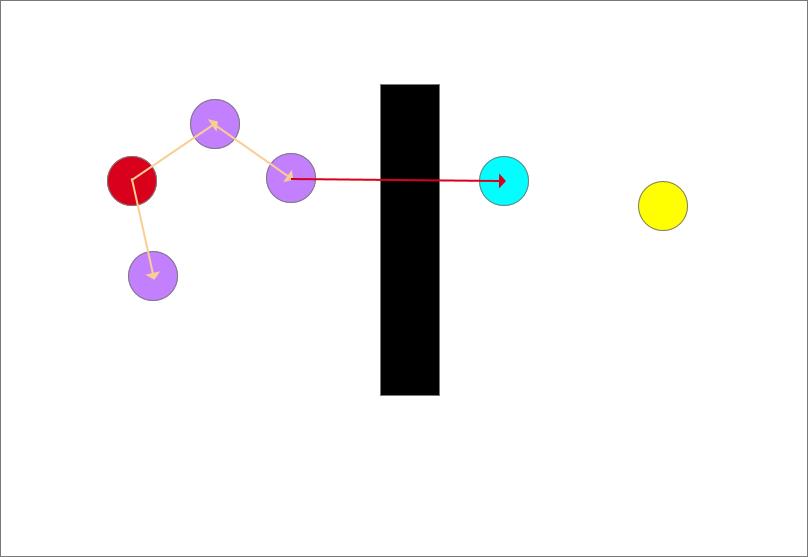
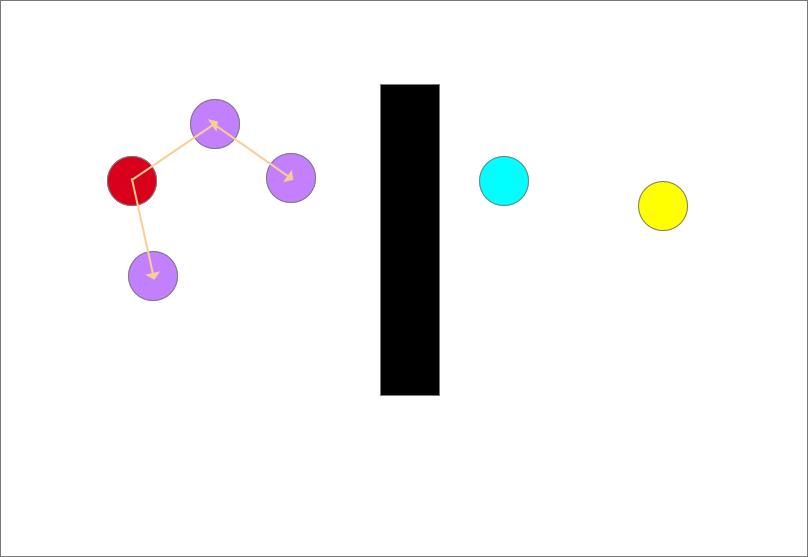
从此时的最近点也就是起点沿着生长方向生长一个步长得到一个生长点(紫色圆),但是生长点都长障碍物里面去了会发生碰撞,生长失败!
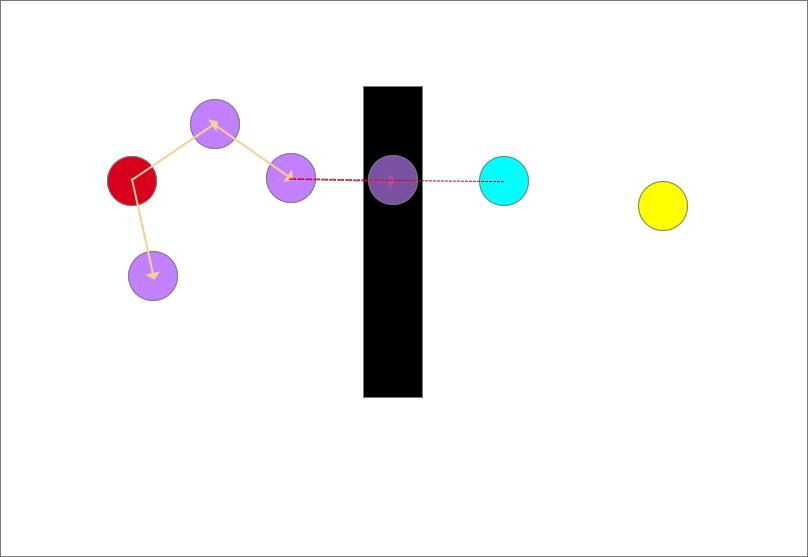
剔除该生长节点,此次生长作废,不合格,树不接受。
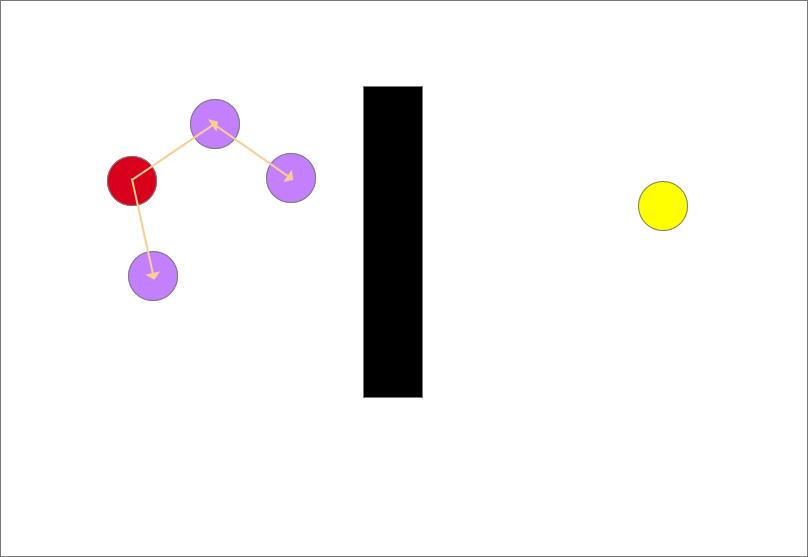
重复以上的步骤,直到有生长节点进入终点的设定邻域
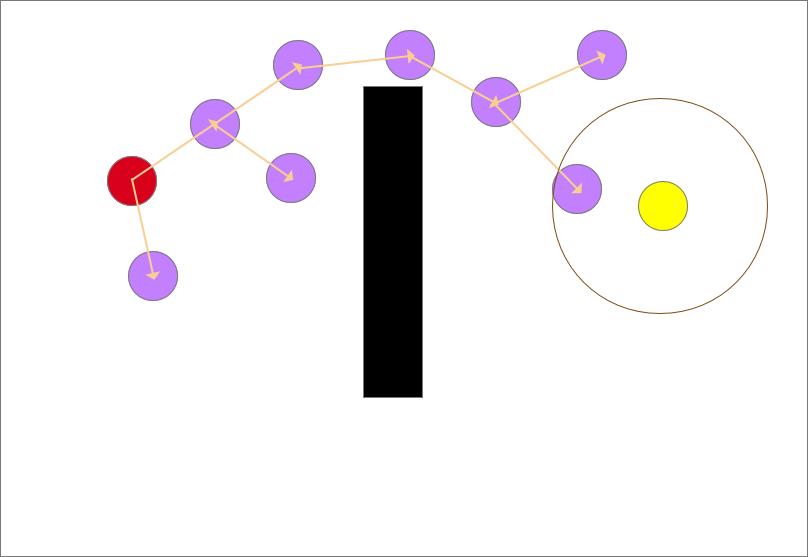
不断追溯它们的父节点,可找到一条从起点到终点的安全路径。如图中绿色线所示
二、RRT算法编写的步骤
1.算法步骤
- 初始化整个空间,定义初始点、终点、采样点数、点与点之间的步长t等信息
- 在空间中随机产生一个点xrand
- 在已知树的点集合中找到距离这个随机点最近的点xnear
- 在xnear到xrand的直线方向上从xnear以步长t截取点xnew
- 判断从xnear到xnew之间是否存在障碍物,若存在则舍弃该点
- 将new点加入到树集合中
- 循环2~6,循环结束条件:有一个new点在终点的设定邻域内
2.算法的实现
- 初始化整个空间,定义初始点、终点、采样点数、点与点之间的步长t等信息
from math import sqrt
import numpy as np
import random
import itertools
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
# 初始化整个空间,定义初始点、终点、采样点数、点与点之间的步长t等信息
x_width = 25 # 空间的长度
y_width = 12 # 空间的宽度
error_list = [[0 for i in range(0, x_width)] for j in range(0, y_width)]
error_list[2][10] = 1
error_list[3][10] = 1
error_list[4][10] = 1
error_list[5][10] = 1
error_list[6][10] = 1
error_list[7][10] = 1
error_list[8][10] = 1
x0 = 6 # 定义初始点的x坐标
y0 = 4 # 定义初始点的y坐标
xn = 17 # 定义终点的x坐标
yn = 5 # 定义终点的y坐标
t = 1 # 点与点之间的步长
error_list[y0][x0] = 4
error_list[yn][xn] = 3
error_list = np.array(error_list)
# print(error_list)
plt.figure()
plt.xlim((-1, x_width))
plt.ylim((-1, y_width))
plt.xlabel('x')
plt.ylabel('y')
plt.xticks(np.arange(x_width))
plt.yticks(np.arange(y_width))
plt.grid()
tree_list = []
tree_list.append([x0, y0, x0, y0]) # 把起点作为树的点放入列表,避免随机点与起点重合
plt.plot(x0, y0, 'ro')
plt.plot(xn, yn, marker='o', color='yellow')
plt.plot([10, 10, 10, 10, 10, 10, 10], [2, 3, 4, 5, 6, 7, 8], 'k-', linewidth='5')
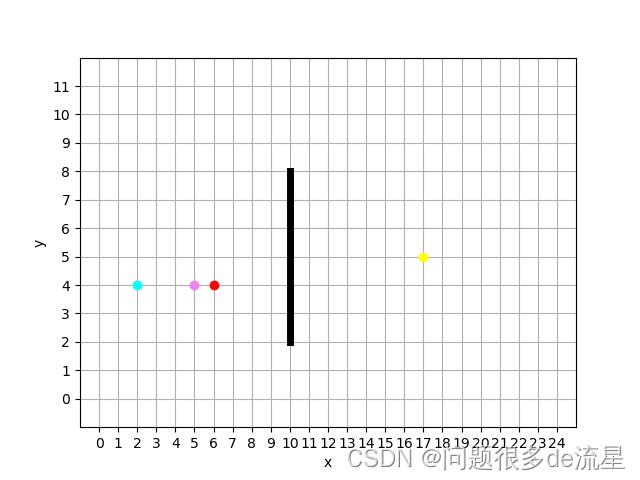
- 在空间中随机产生一个点xrand,这个点不能在tree_list里面,构建一个函数
# 在空间中随机产生一个点xrand ->这个点不能是起点
def product_rand(tree_list):
x_width = 25 # 空间的长度
y_width = 12 # 空间的宽度
random_point = list(itertools.product(range(0, x_width), range(0, y_width)))
xrand = random.sample(random_point, 1)
xrand = list(xrand[0]) # 将随机点转换成list形式
tree_list = np.array(tree_list)
tree = tree_list[:, 0:2]
while xrand in tree: # 如果随机点在树的点列表里,重新生成随机点
xrand = random.sample(random_point, 1)
xrand = list(xrand[0]) # 将随机点转换成list形式
return xrand
- 在已知树的点集合中找到距离这个随机点最近的点xnear,构建一个函数
# 在已知树的点集合中找到距离这个随机点最近的点xnear
def product_near(tree_list, xrand):
m = np.inf
for i in range(0, len(tree_list)):
if abs(tree_list[i][0] - xrand[0]) + abs(tree_list[i][1] - xrand[1]) < m:
m = abs(tree_list[i][0] - xrand[0]) + abs(tree_list[i][1] - xrand[1])
xnear = [tree_list[i][0], tree_list[i][1]]
return xnear
- 确定方向:在xnear到xrand的直线方向上从xnear以步长t截取点xnew,构建一个函数
def decide_direction(xrand, xnear, t):
z_value = sqrt((xnear[0] - xrand[0]) ** 2 + (xnear[1] - xrand[1]) ** 2) # 斜边长度
cos_value = (xrand[0] - xnear[0]) / z_value
sin_value = (xrand[1] - xnear[1]) / z_value
xnew = [(xnear[0] + t * cos_value), (xnear[1] + t * sin_value)]
return xnew
- 判断从xnear到xnew之间是否存在障碍物,若存在则舍弃该点
xrand = product_rand(tree_list) # 随机生成点
xnear = product_near(tree_list, xrand)
xnew = decide_direction(xrand, xnear, t)
if xnear[0] != xrand[0]:
k = (xrand[1] - xnear[1]) / (xrand[0] - xnear[0])
y = k * (10 - xnear[0]) + xnear[1]
else:
y = 0
while 10 <= max(xnear[0], xnew[0]) and 10 <= min(xnear[0], xnew[0]) and 2 <= y <= 8:
xrand = product_rand(tree_list) # 随机生成点
xnear = product_near(tree_list, xrand)
xnew = decide_direction(xrand, xnear, t)
if xrand[0] - xnear[0] != 0:
k = (xrand[1] - xnear[1]) / (xrand[0] - xnear[0])
y = k * (10 - xnear[0]) + xnear[1]
tree_list.append([xnew[0], xnew[1], xnear[0], xnear[1]])
plt.plot(xrand[0], xrand[1], marker='o', color='cyan')
plt.plot(xnew[0], xnew[1], color='violet', marker='o')
- 循环,循环结束条件:有树节点在终点的设定固定邻域之内
# 循环
while ((xnew[0] - xn) ** 2 + (xnew[1] - yn) ** 2) > 1:
xrand = product_rand(tree_list) # 随机生成点
xnear = product_near(tree_list, xrand)
xnew = decide_direction(xrand, xnear, t)
if xnear[0] != xrand[0]:
k = (xrand[1] - xnear[1]) / (xrand[0] - xnear[0])
y = k * (10 - xnear[0]) + xnear[1]
else:
y = 0
while 10 <= max(xnear[0], xnew[0]) and 10 <= min(xnear[0], xnew[0]) and 2 <= y <= 8:
xrand = product_rand(tree_list) # 随机生成点
xnear = product_near(tree_list, xrand)
xnew = decide_direction(xrand, xnear, t)
if xrand[0] - xnear[0] != 0:
k = (xrand[1] - xnear[1]) / (xrand[0] - xnear[0])
y = k * (10 - xnear[0]) + xnear[1]
tree_list.append([xnew[0], xnew[1], xnear[0], xnear[1]])
plt.plot(xrand[0], xrand[1], marker='o', color='cyan')
plt.plot(xnew[0], xnew[1], color='violet', marker='o')
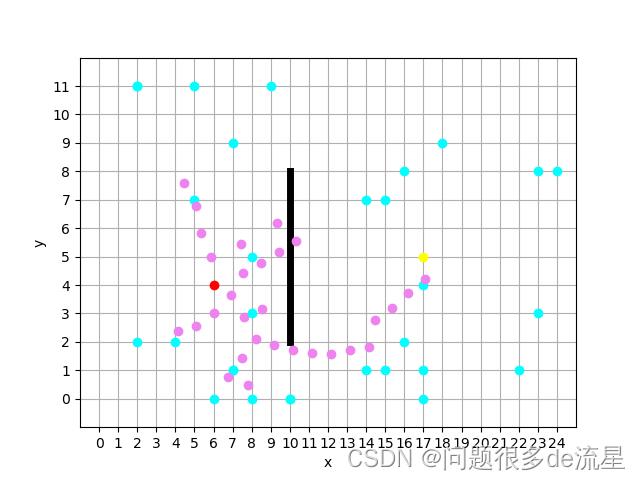
- 循环以找到父节点,将这些点保存在routine_list列表中,并可视化
tree_list = np.array(tree_list)
routine_list = [[xn,yn]]
n = len(tree_list)-1
x = tree_list[n,0]
y = tree_list[n,1]
f_x = tree_list[n,2]
f_y = tree_list[n,3]
routine_list.append([x,y])
search_list=[]
while [x0,y0] not in routine_list:
search_list = tree_list[np.where((tree_list[:,0]==f_x) & (tree_list[:,1]==f_y))][0]
search_list = search_list.tolist()
routine_list.append([search_list[0],search_list[1]])
f_x = search_list[2]
f_y = search_list[3]
print(routine_list)
routine_list = np.array(routine_list)
plt.plot(routine_list[:,0], routine_list[:,1], '-', linewidth='2')
plt.show()
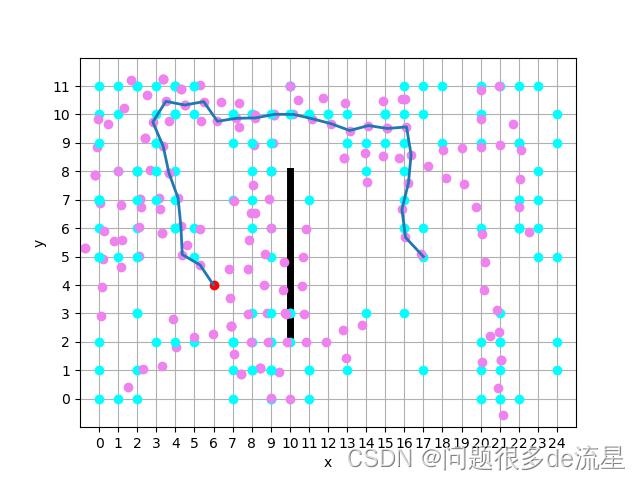
三、RRT*算法编写的步骤
RRT算法只能找到一条可行路径,并不能保证找到一条最优路径,RRT* 算法在RRT算法的基础上增加了两步:rewrite和random relink。也就是重写和随机重连。
重写就是在新节点xnew加入到树种之后,重新为它选择父节点,好让它到起始点的路径长度(代价)更小。
随机重连就是在重写完成之后,对新节点xnew附近一定范围内的节点进行重连。重连就是,检查一下如果把xnew附近的这些节点的父节点设置为xnew,这些节点的代价会不会减小。如果能够减小,就把这些节点的父节点更改为xnew;否则,就不更改。RRT* 算法考虑每一个节点到出发点的距离,为此每一个节点会增加一个属性:distance_to_start,即到出发点的距离。相应地在每一个节点选择父节点地时候,新节点的距离等于父节点的距离加上父节点到子节点的直线距离。
1.算法的步骤
在RRT的基础上增加两个功能:
①rewrite重写
遍历整个树,
获得到新节点xnew的距离小于一定阈值(比如1.5倍的步长,也就是1.5*t)的所有节点
将这些节点加入到一个名为candidate_parent_of_newpoint的列表中,
为了方便,这些节点的distance不再用来存储到出发点的距离,而是用来存储如果把该节点设置为xnew的父节点的话,xnew到出发点的距离。
找到candidate_parent_of_newpoint列表中具有最小distance的那个节点,返回他的索引index,将新节点newpoint的父节点设置为index。
②random relink
遍历整个列表,对每一个节点执行如下动作
if(该节点到xnew的距离小于一定的阈值,比如1.6倍的步长,也就是1.6*t)
if(该节点现在的distance>把该节点的父节点更新为newpoint之后的distance)
把该节点的父节点设置为xnew,并更新该节点的distance值
更新以该节点为根节点的子树中的每个节点的distance。
2.算法的实现
rewrite(重写):
# rewrite重写
def rewrite(tree_list, t, xnew):
# 遍历整个树
candidate_parent_of_xnew = []
for i in range(0, len(tree_list)):
distance = sqrt((xnew[0] - tree_list[i][0]) ** 2 + (xnew[1] - tree_list[i][1]) ** 2)
# 获得新节点xnew的距离小于一定阈值(比如1.5倍步长,也就是1.5*t)所有节点
if distance < 1.5 * t and (xnew[0] != tree_list[i][0] or xnew[1] != tree_list[i][1]):
distance = tree_list[i][4] + distance
candidate_parent_of_xnew.append([tree_list[i][0], tree_list[i][1], distance])
candidate_parent_of_xnew = np.array(candidate_parent_of_xnew)
# 将这些节点加入到candidate_parent_of_xnew列表中
parent_point = candidate_parent_of_xnew[np.where(candidate_parent_of_xnew[:, 2] == candidate_parent_of_xnew[:, 2].min())]
tree_list.append([xnew[0], xnew[1], parent_point[0][0], parent_point[0][1], parent_point[0][2RRT快速随机搜索树
快速扩展随机树(Rapidly-exploring Random Trees,RRT)算法,是近十几年得到广泛发展与应用的基于采样的运动规划算法,它由美国爱荷华州立大学的Steven M. LaValle教授在1998 年提出。RRT 算法是一种在多维空间中有效率的规划方法。原始的RRT 算法是通过一个初始点作为根节点,通过随机采样,增加叶子节点的方式,生成一个随机扩展树,当随机树中的叶子节点包含了目标点或进入了目标区域,便可以在随机树中找到一条由树节点组成的从初始点到目标点的路径。
RRT是一种通过随机构建空间填充树来有效搜索非凸,高维空间的算法。树是从搜索空间中随机抽取的样本逐步构建的,并且本质上倾向于朝向大部分未探测区域生长。由于它可以轻松处理障碍物和差分约束(非完整和动力学)的问题,并被广泛应用于自主机器人运动规划。
RRT也可以被看作是一种为具有状态约束的非线性系统生成开环轨迹的技术。一个RRT也可以被认为是一个蒙特卡罗方法。用来将搜索偏向一个配置空间中图形的最大Voronoi区域。一些变化甚至可以被认为是随机分形。
改进的RRT算法:
-
基于概率P的RRT;
-
RRT_Connect’
-
RRT*;
-
Parallel-RRT;
-
Real-time RRT;
-
Dynamic domain RRT;
基于RRT的运动规划算法综述
介绍:
在过去的十多年中, 机器人的运动规划问题已经收到了大量的关注,因为机器人开始成为现代工业和日常生活的重要组成部分。最早的运动规划的问题只是考虑如何移动一架钢琴从一个房间到另一个房间而没有碰撞任何物体。早期的算法则关注研究一个最完备的运动规划算法(完备性指如果存在这么一条规划的路径,那么算法一定能够在有限时间找到它),例如用一个多边形表示机器人,其他的多边形表示障碍物体, 然后转化为一个代数问题去求解。 但是这些算法遇到了计算的复杂性问题,他们有一个指数时间的复杂度。在 1979 年,Reif则证明了钢琴搬运工问题的运动规划是一个 PSPACE-hard 问题[1]。所以这种完备的规划算法无法应用在实际中。
在实际应用中的运动规划算法有胞分法[2],势场法[3],路径图法[4]等。这些算法在参
数设置的比较好的时候,可以保证规划的完备性,在复杂环境中也可以保证花费的时间上限。然而,这些算法在实际应用中有许多缺点。
例如在高维空间中这些算法就无法使用, 像胞分法会使得计算量过大。 势场法会陷入局部极小值,导致规划失败[5],[6]。
基于采样的运动规划算法是最近十几年提出的一种算法,并且已经吸引了极大的关注。
概括的讲,基于采样的运动规划算法一般是连接一系列从无障碍的空间中随机采样的点,试图建立一条从初始状态到目标状态的路径。
与最完备的运动规划算法相反,基于采样的方法通过避免在状态空间中显式地构造障碍物来提供大量的计算节省。即使这些算法没有实现完整性, 但是它们是概率完备, 这意味着规划算法不能返回解的概率随着样本的数量趋近无穷而衰减到零[7],并且这个下降速率是指数型的。
快速扩展随机树(Rapidly-exploring Random
Trees, RRT)算法,是近十几年得到广泛发展
与应用的基于采样的运动规划算法,它由美国爱荷华州立大学的
Steven
M. LaValle教授在1998 年提出, 他一直从事 RRT 算法的改进和应用研究,他的相关工作奠定了 RRT 算法的基础。 RRT 算法是一种在多维空间中有效率的规划方法。原始的 RRT 算法是通过一个初始点作为根节点,通过随机采样,增加叶子节点的方式,生成一个随机扩展树,当随机树中的叶子节点包含了目标点或进入了目标区域,便可以在随机树中找到一条由树节点组成的从初始点到目标点的路径。
快速扩展随机树(RRT) 也是一种数据结构和算法,其设计用途是用来有效搜索高维非
凸空间,可应用于路径规划、虚拟现实等研究。
RRT 是一种基于概率采样的搜索方法,它采用一种特殊的增量方式进行构造,这种方式能迅速缩短一个随机状态点与树的期望距离。该方法的特点是能够快速有效的搜索高维空间,通过状态空间的随机采样点,把搜索导向空白区域,从而寻找到一条从起始点到目标点的规划路径。它通过对状态空间中的采样点进行碰撞检测,避免了对空间的建模,能够有效的解决高维空间和复杂约束的路径规划问题。
RRT算法适合解决多自由度机器人在复杂环境下和动态环境中的路径规划问题[8]。与其他的随机路径规划方法相比, RRT 算法更适用于非完整约束和多自由度的系统中[9]。
相比于最原始的
RRT 算法的一些缺点,又提出了许多改进的 RRT 算法,例如:
-
基于概率 P
的 RRT
为了加快随机树到达目标点的速度,简单的改进方法是:在随机树每次的生长过程中,根据随机概率(0.0 到 1.0 的随机值 p)来选择生长方向是目标点还是随机点。2001 年,LaValle在采样策略方面引入 RRT GoalBias与 RRT GoalZoom, RRT GoalBias方法中,规划器随机采样的同时,以一定概率向最终目标运动;RRTGoalZoom方法中,规划器分别在整个空间和目标点周围的空间进行采样[10]。
-
RRT_Connect
RRT_Connect即连接型 RRT, 2000 年由 LaValle教授和日本东京大学的 Kuffner教授联合提出。该算法一开始同时从初始状态点和目标状态点生长两棵随机树,每一次迭代过程中,其中一棵树进行扩展,尝试连接另一棵树的最近节点来扩展新节点。然后,两棵树交换次序重复上一迭代过程[10]。这种双向的 RRT 技术具有良好的搜索特性,相比原始快速扩展随机树算法,在搜索速度、搜索效率有了显著提高。
-
RRT*
2010
年, MIT 的 Sertac和 Emilio 证明了在基于采样的运动规划算法中,随着 RRT 算法采样点趋向于无穷,其收敛到最优解的概率为 0,为此他们提出了渐进最优(asymptoticoptimality)的 RRT*算法[11]。该算法在原有 RRT 算法基础上,改进了父节点选择的方式,采用代价函数来选取扩展节点邻域内最小代价的节点为父节点,同时,每次迭代后都会重新连接现有树上的节点,从而保证计算复杂度和渐进最优解。
定义:
位姿空间:
运动规划的状态空间是应用于机器人变换的集合,称为位姿空间(configuration space),
引入了 C-空间、 C-空间障碍物、自由空间等一系列概念, Latombe在他的著作[12]中对路径规划的文献进行了总结统一。对于路径规划问题,位姿空间的引入是一次划时代的革命,一旦清楚的理解了位姿空间的概念和意义,许多诸如几何学、运动学等各种以不同形式出现的运动规划问题都可以采用相同的规划算法加以解决,这种层次的抽象是非常重要的。
下面介绍一些概念:
定义
2.1 位姿(configuration) 机器人一个位姿指的是一组相互独立的参数集,它能完
全确定机器人上所有的点在工作空间
W 中的位置,这些参数用来完整描述机器人在工作空间 W 中的状态。一个位姿通常表示为带有位置和方向参数的一个向量(vector),用 q 表示。
定义
2.2 自由度(degrees of freedom) 机器人的自由度定义为机器人运动过程中决定其运动状态的所有独立参数的数目,即
q 的维数。
定义
2.3 位姿空间(configuration space) 位姿空间是机器人所有可能位姿组成的集合,
代表了机器人所有可能的运动结果,称为
C-空间,也可简记为 C。
定义
2.4 距离函数(distance function) C-空间中的距离函数定义为该空间中的一个映射。记为。
障碍物空间和自由空间
假设在工作空间中包含所有的障碍物区域,定义 A 为机器人, A的具体的含义可以理解为从机器人位姿空间到机器人工作空间的一一映射,它将位姿空间中的任意一个点映射成
2 维或者3 维工作空间中机器人各刚体段的位姿状态。
定义
2.5 障碍物空间(obstacle space) 表达式定义了位姿空间当中的障碍物空间。
位姿空间中的无碰撞区域通常称为自由空间,可用与集合运算定义(表示集合 A
与 B 的差集)
定义
2.6 自由空间(free space) 表达式定义了位姿空间中的自由空间。
定义
2.7 路径长度(path cost) 定义pc:为一条路径的非负长度。表示所有自由空间中的路径集合。
2.3
运动规划的基本定义
用 C-空间的思路,运动规划问题在概念上变得非常简单:任务是在中寻找一条从起始
位姿到目标位姿的路径。 运动规划问题的示意图如图
2.1 所示,图中整个水滴表示位姿空间
图1运动规划示意图
有了上述概念,
C-空间中的运动规划问题可描述如下:
-
定义一个工作空间 W;
-
定义 W 中的障碍物区域 O 和机器人
A;
-
所有可能的机器人位姿构成 C-空间,并且划分为和;
-
指定机器人初始位姿和目标目标位姿;
-
可行规划(Feasible planning) 一个完整的算法必须计算一条连续的路径,使得,或者正确报告这样的路径不存在。
-
最优规划(Optimal planning) 在所有的可行的规划的路径里面花费代价最少的一条路径,或者报告这样的路径不存在。
算法:
在介绍
RRT 算法之前,先说明一下路径的表示方法。 我们用一个有向图来表示路径
G=(V,E), 那么一条可行的路径就是一个顶点的序列,,。同时,表示边。 这样子问题就变成了使用采样到的点来扩展图 G,使之能找到一条从初始节点到达目标节点的路径。
3.1
原始的 RRT 算法
算法1:RRT算法主体部分
While do
算法2:原始RRT算法的Extend函数
If then
这里可以看到两个算法,
一个是算法的主体部分,还有一个是 RRT
算法的 Extend 函数,主要是如何利用从采样到点扩展图 G。下面详细介绍每一步骤:
初始化顶点为,边集E;
进入while循环,迭代N次停止;
设置了为新的图G;
Sample(i)采样一个新的点;
利用新的点扩展图G.
原始RRT算法Extend函数的步骤:
把V,E暂存
函数表示求图G
中离欧式距离最近的点;一般情况下会采用来存储图中的节点,这样会节约搜索的时间。
表示存在一个点它将最小化但是,为我们人为设定的一个值, 其实就是往 q 方向步进了一段距离;
进行碰撞检测, 然后判断这一段路径,是否与障碍物发生碰撞即判断路径是否属于中;
把加到顶点集中;
把加入到边集中;
返回扩展后的图。
从算法中可以看出,
RRT 的扩展能够趋向于位姿空间中没有扩展到的部分。这就决定了RRT 一开始能够快速的进行扩展,而且能够形成对空间的全面覆盖。
RRT 顶点是分配在位姿空间中是一致均匀的,如果路径存在,在顶点数目一定的条件下是肯定可以找到一条路径的。
当然 RRT 算法也有一些缺点,它是一种纯粹的随机搜索算法对环境类型不敏感,当
C 中包含大量障碍物和狭窄通道约束时,算法的收敛速度慢, 效率会大幅下降。
为了加快随机树到达目标点的速度,简单的改进方法是:在随机树每次的生长过程中,根据随机概率(0.0 到1.0 的随机值 p)来选择生长方向是目标点还是随机点。
基于概率P的RRT
算法3:基于概率P的RRT算法的Extend函数
1.
If then
Return
算法主要的改变就是在于
Extend 函数时, 增加了一个ChoseTarget函数。这个函数不会全都使用作为扩展的方向,而是一个概率P来选择进行扩展,以1-P的概率选择来进行扩展。这样的好处就会加快了收敛速度, 不过需要选择好对应的 P 概率。
3.3
RRT_Connect算法
上述的
RRT 每次搜索都只有从初始状态点生长的快速扩展随机树来搜索整个状态空间,
如果从初始状态点和目标状态点同时生长两棵快速扩展随机树来搜索状态空间,效率会更高。为此,
在 2000 年由 LaValle教授和日本东京大学的 Kuffner教授联合提出了基于双向扩展平衡的连结型双树RRT 算法,即 RRT_Connect算法。 算法如下所示:
算法4:RRT_Connet算法
While do
If then
;
If then
Do
If then
Else break;
While not
If then return ;
If then Swap;
该算法与原始
RRT 相比, 在目标点区域建立第二棵树进行扩展。 每一次迭代中,
开始步骤与原始的 RRT
算法一样,都是采样随机点然后进行扩展。
然后扩展完第一棵树的新节点后,以这个新的目标点作为第二棵树扩展的方向。同时第二棵树扩展的方式略有不同,首先它会扩展第一步得到,如果没有碰撞,继续往相同的方向扩展第二步,直到扩展失败或者表示与第一棵树相连了, 即 connect 了,整个算法结束。 当然每次迭代中必须考虑两棵树的平衡性,即两棵树的节点数的多少(也可以考虑两棵树总共花费的路径长度), 交换次序选择“小”的那棵树进行扩展。 这种双向的 RRT 技术具有良好的搜索特性,比原始 RRT 算法的搜索速度、搜索效率有了显著提高,被广泛应用。首先,
Connect
算法较之前的算法在扩展的步长上更长,使得树的生长更快;其次,两棵树不断朝向对方交替扩展,而不是采用随机扩展的方式,特别当起始位姿和目标位姿处于约束区域时,两棵树可以通过朝向对方快速扩展而逃离各自的约束区域。这种带有启发性的扩展使得树的扩展更加贪婪和明确,使得双树RRT 算法较之单树RRT 算法更加有效。
3.4
RRT*算法
2010
年, MIT 的 Sertac和 Emilio 提出了 RRT*算法。这个算法与上面的算法相比,不但可以找到可行解,还可以找到一条相对次优的算法。
Extend 函数的算法如下:
算法5:RRT*算法的Extend
If then
For all do
If then
If then
For all do
If and
Return
这个算法增加了一些函数,
先来讲解下增加的函数的作用。表示这两个点
直接相连的一条路径。函数表示从到的路径花费。函数则返回 q
节点的父亲节点。 near 函数是 RRT*里最关键的一步, 他会返回一个顶点的集合,表示这些顶点是靠近的。它以为球心的,为半径的超球体,这些顶点就包括在超球体的内部,一般取,和是常数,表示节点维度的数,表示所有节点的个数[11]。
然后来分析这个算法的步骤:
前几步采样扩展步长与之前类似,只是当扩展出新的步长的时候,用 near 函数求邻近点。遍历邻近点集合,寻找花费代价最小的节点,把加入到边集中。 最后还要进行一步回溯的操作, 即如果存在这么一条路径经过到达所需的花费少于经过的parent 到达的花费,那么就可以说明原来到的路径不是最优的, 需要选择经过到达的路径作为新路径。 对所有的邻近点集合内的点都做相同的操作。 这样经过 N 次迭代后得到就是接近最优的次优路径了。
4.结语
RRT
算法是目前流行的基于增量采样的运动规划算法。
本文介绍了它的原始算法和其他RRT
算法的变种。 为了优化 RRT 算法的收敛速度问题提出概率 P 选择的 RRT 和 RRT-Connect算法。 还有为止还有仍在研究的基于多树扩展的 RRT 算法。 针对 RRT 难以得到最优解, 而提出的 RRT*算法可以得到接近最优的次优解。 RRT 算法的优势简单易实现,可以运用在高维的运动规划中,并且采样数量足够多情况下总可以找到可行解,因为是随机采样可以避免陷入局部极小。
当然他也有不足,比如 RRT
算法收敛的速率是未知的, 找树最邻近点的效率上,同时还存在一个“长尾”效应比如刚开始扩展的一些点是有用的,后面随机采样的点可能完全用不到完全是浪费时间的。
还有许多 RRT
算法的变种本文未介绍,比如利用当下流行的
GPU 并行计算加速 RRT 求解速度的 Parallel-RRT 算法,改进实时性的 real-time RRT,针对动态环境的
dynamic
domain RRT 算法等等。
希望以后对 RRT
算法开展更深入的研究。
参考文献:
https://en.wikipedia.org/wiki/Rapidly-exploring_random_tree
http://planning.cs.uiuc.edu/
以上是关于RRT与RRT*算法具体步骤与程序详解(python)的主要内容,如果未能解决你的问题,请参考以下文章
三维路径规划基于matlab RRT算法无人机三维路径规划含Matlab源码 1363期