Mechine Learning 机器学习笔记

Posted 2023-01-21 OUC_Shizue

笔记作者:OUC_Shizue 参考课程:复旦大学 邱锡鹏 《神经网络与深度学习》

第一章：机器学习概论

一、机器学习的定义

1、直接定义

​ 机器学习≈计算机自动构建映射函数

​ Machine Learning 是指从有限的观测数据中学习出具有一般性的规律，并利用这些规律对未知数据进行预测的方法

2、为什么要机器学习

​ 现实世界问题复杂，通过人工总结规律构建映射较为困难；因此我们将其转化为提供数据样本让计算机自动总结规律，构建映射。

3、如何构建输入输出函数

​ 从大量数据中学习规律——function;

​ 即x(representation)->y(label)，如果x，y服从分布P(x,y)，则从分布中取样作为train data，接着构造假设空间F，即一系列f(x)构成的函数族，从中选出最能符合train data映射关系的f’(x)，但此时f’(x)为仅在train data上得到的拟合函数，对该data之外的数据预测效果未知，机器学习的目的就在于让该f’(x)对一切x均有较好预测效果。

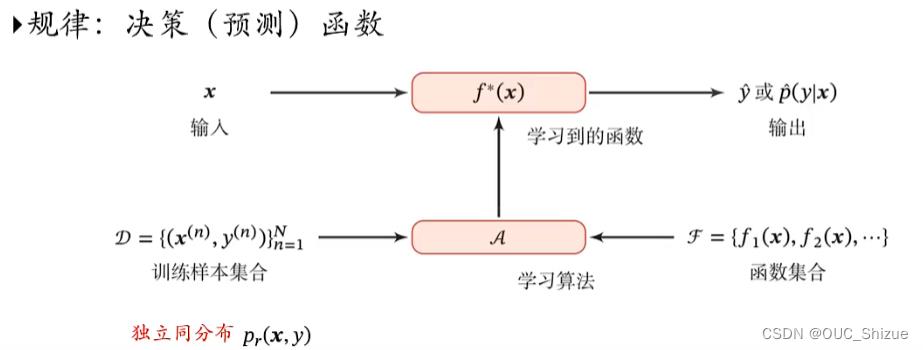
4、表示学习介绍

（1）局部表示

​ one-hot：一维表示，依赖与知识库、规则

例如：

• A：[1,0,0,0]
• B：[0,1,0,0]
• C：[0,0,1,0]
• D：[0,0,0,1]

K个元素可以表示K个语义

（2）分布式表示

• 多维度表示，例如RGB表示所有颜色，k个元素表示2的k次方个语义。
• 特点：压缩、低维、稠密向量
• 可将one-hot向量嵌入到空间从而转化为分布式表示。

二、机器学习的类型

1、监督学习

（1）回归问题 Regression

• 房价预测
• 股票预测

（2）分类问题 Classification

• 手写体数字识别
• 人脸识别
• 垃圾邮件检测

2、无监督学习

（1）聚类 Clustering

​ 给一些x让计算机自动分类，让类内样本相似，类间样本各不相似

（2）降维 Dimensionality Reduction

​ 将平面数据投影到二维空间，让相似样本距离较近，便于可视化

（3）密度估计 Density Estimation

​ 给定一个空间，将空间内任意一点的密度函数p(x)估计出来

3、强化学习

​ 通过与环境进行交互来学习，例如AlphaGo在下棋过程中以输赢来作为指标

三、机器学习的要素

• 数据：连续用回归，离散用分类，只给x用无监督；同时需要抽取特征，自动抽取则为表示学习
• 模型：给定假设空间，从中选择最优模型，对x预测y达到最优效果
• 学习准则：通过一个准则判断学习效果的好坏
• 优化算法：给定一个准则后对模型进行优化

四、泛化与正则化

1、泛化误差

• 经验风险-期望风险=泛化误差
• 若经验风险过大，期望风险过小，则泛化误差较大，发生过度拟合；因此机器学习的目标为经验风险低，同时泛化误差低

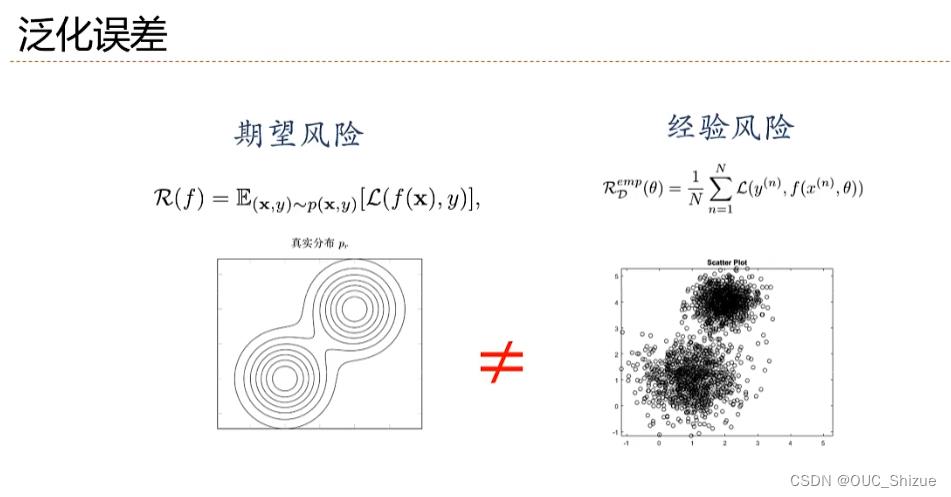
2、优化与正则化的目标

（1）优化

​ 选出一个模型使得经验风险最小，但此时模型往往过拟合，即泛化误差较大

（2）正则化

​ 降低模型复杂度，减小泛化误差

3、正则化 Regularization

（1）定义

​ 所有损害优化的方法都是正则化

（2）方法

• 增加优化约束：L1/L2约束、数据增强（构造一些新样本，干扰优化）
• 干扰优化过程：权重衰减、随机梯度下降、提前停止（使用一个验证集Validation Dataset来测试每次迭代的参数在验证集上是否为最优，如果在验证集上的错误率不再下降则停止迭代）

五、线性回归

1、回归 Regression

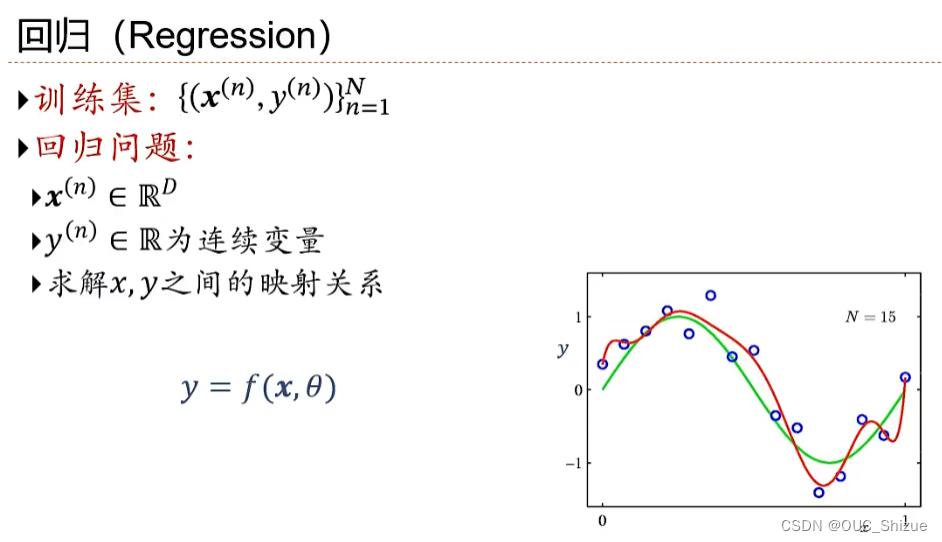
2、线性回归 Linear Regression

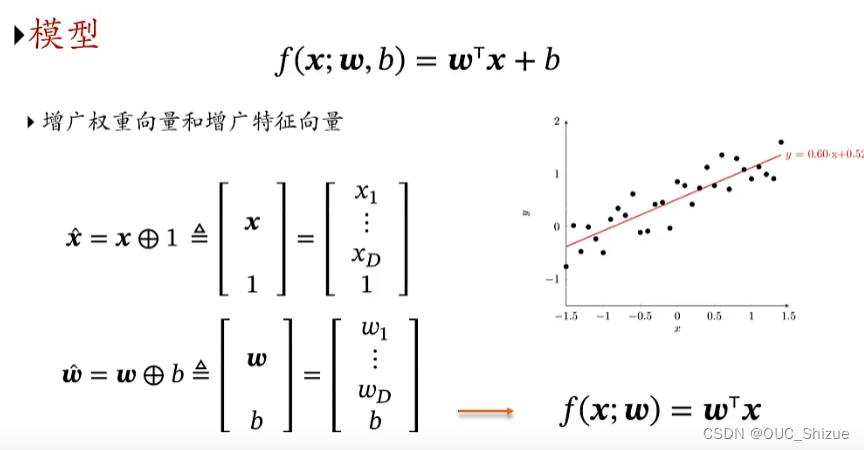
⊕表示拼接，即在增广矩阵末尾加上该数

3、经验风险最小化 Empirical Risk Minimization，ERM

4、矩阵微积分部分知识

5、结构风险最小化 Structure Risk Minimization，SRM

• 对应概率中的岭回归 Ridge Regression
• 当特征之间存在共线性时，X*X转置不可逆，因此通过一个正则化项对w进行约束

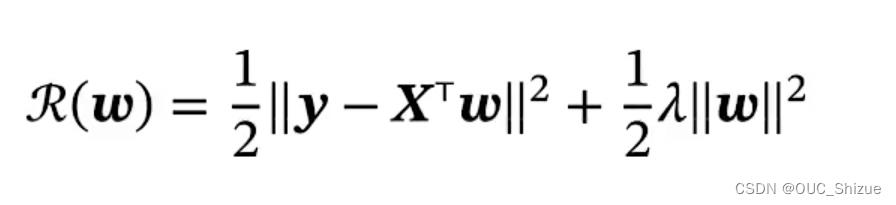
6、概率角度看线性回归

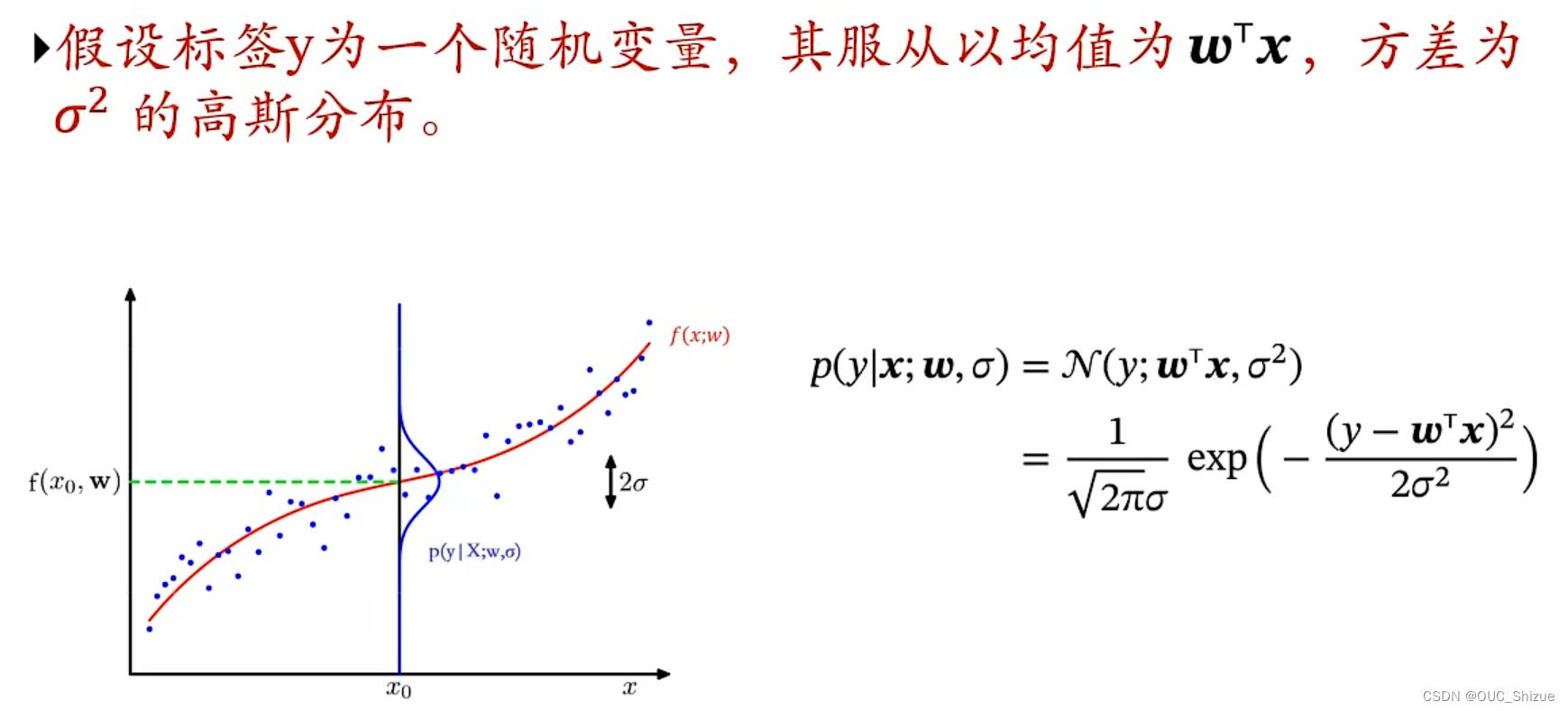
（1）似然函数 Likelihood

（2）线性回归中的似然函数

（5）最大似然估计 Maximum Likelihood Estimate，MLE

• 目标为在给定每一x时，得到标签y的似然最大，即样本中所有似然的连乘最大。
• 在机器学习中似然常常与指数相关，因此引入log简化计算；例如每个概率为0.01，如果有100个样本则为0.01的100次方，联合概率过小，会产生计算误差
• 引入log的似然函数也称对数似然函数
• 最大似然估计的解与最小二乘一致，因此可以理解为最大似然估计与经验风险最小化两种方法等价

（6）贝叶斯视角

贝叶斯学习

贝叶斯公式

​ 即条件概率公式的变形，使得p(x|y)与p(y|x)能够相互转化

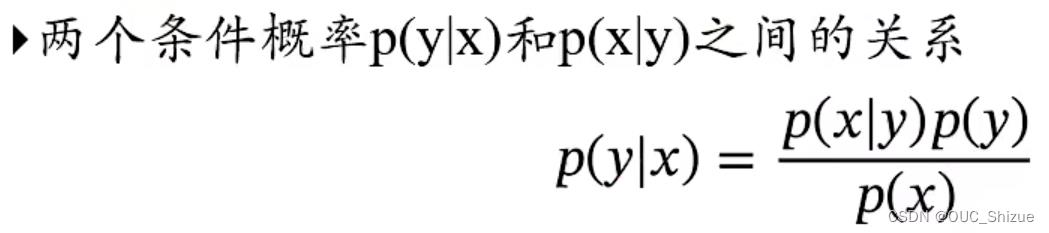
后验(posterior)、似然(likelihood)、先验(prior)

​ p(w|x)∝p(x|w)p(w) 后验∝似然*先验

贝叶斯估计 Bayesian Estimation

​ 代入得

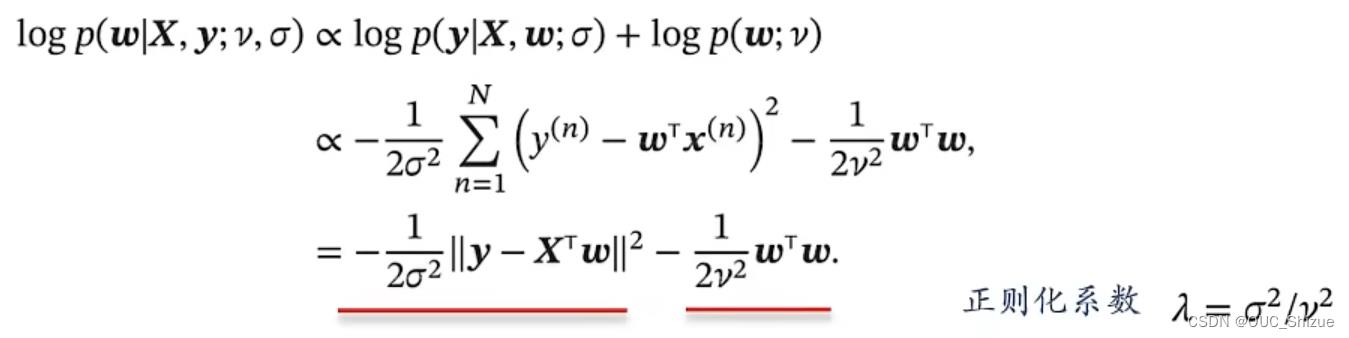
最大后验估计 Maximum A Posteriori Estimation，MAP

​ 求解得到下式，其与结构风险最小化对应

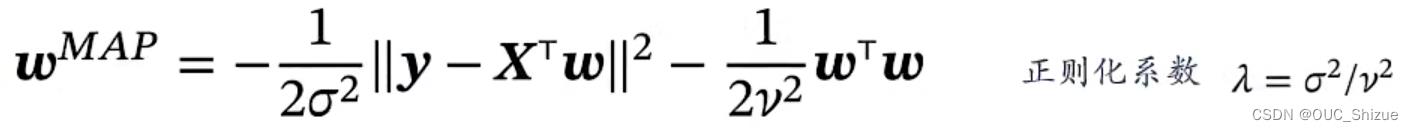
7、四种准则总结

​ 平方误差与概率一一对应，上面理解为对最大值进行限制，下面理解为对w服从以0为中心的高斯分布

平方误差：

• 经验风险最小化
• 结构风险最小化

概率：

• 最大似然估计
• 最大后验估计

六、多项式回归

1、曲线拟合 Curve Fitting

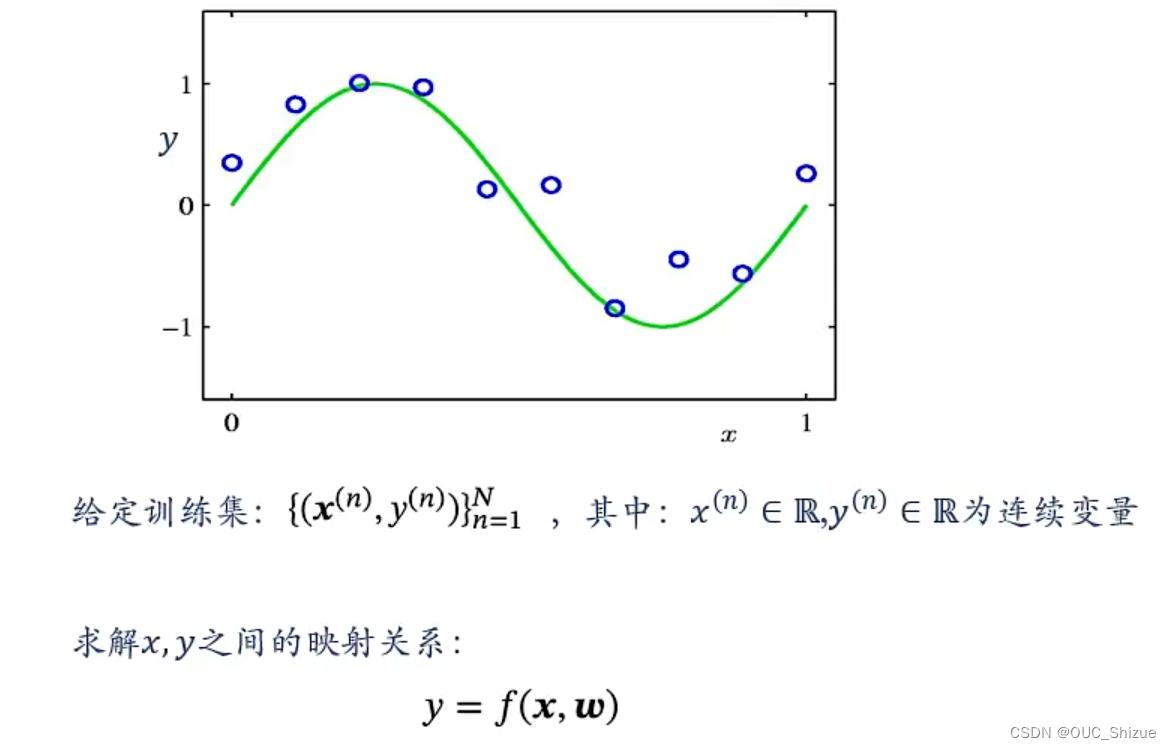
2、平方误差 Sum-of-Squares

3、如何选择多项式次数 Degree

​ 实质上为模型选择问题(Model Selection Problem)，如果次数太低则欠拟合，太高则过拟合。例如下图中曲线次数选择为9次，穿过了所有训练样本，但在x发生细小波动时结果便产生巨大波动，因为展开次数过大，较小项需要很大系数才能对图像产生影响，因此函数图像边缘出现较大极值。

4、控制过拟合：正则化 Regularization

（1）惩罚大系数

​ 由于存在政策化项，因此此处R(w)为结构风险

​ 引入λ=-18以后例题中曲线拟合效果，可见相较于引入超参数之前，过拟合现象得到了较好控制

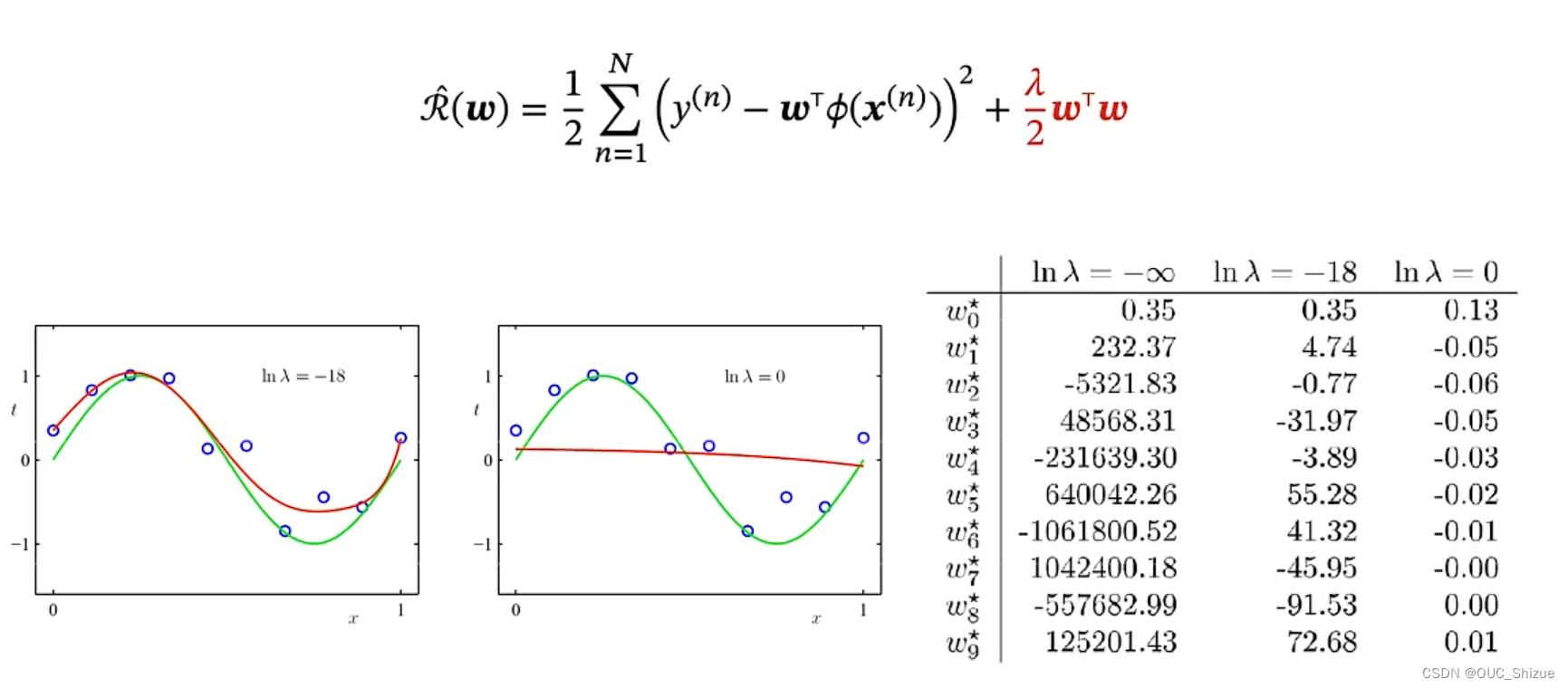
（2）增加train data数量

​ 此处为大数定律的体现，当样本数量无限大的时候经验风险就趋向与期望风险

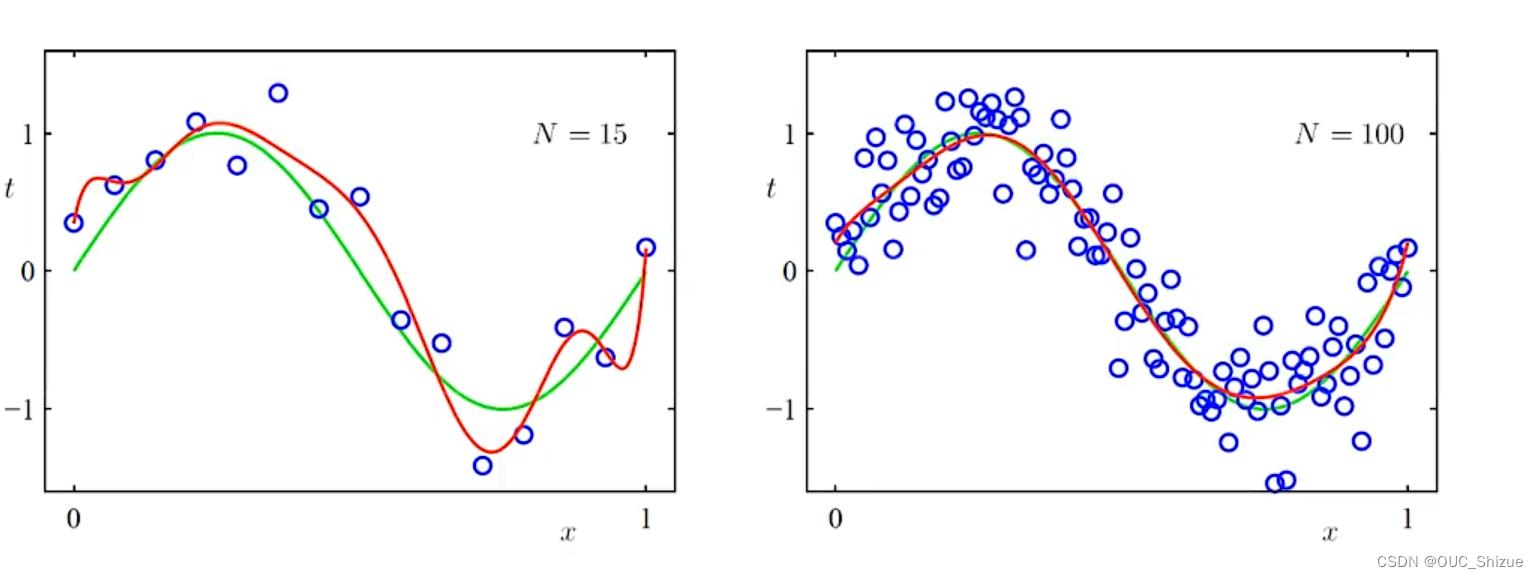
七、模型选择与“偏差-方差”分解

1、模型选择

• 拟合能力强的模型一般复杂度会比较高，容易过拟合
• 如果限制模型复杂度，降低拟合能力，可能会欠拟合

2、如何选择模型

• 模型越复杂，训练错误越低
• 不能根据训练错误最低来选择模型
• 在选择模型时，测试集不可见

3、引入验证集 Validation Set/Development Set

（1）将训练集分为两部分

• 训练集 Training Set
• 验证集 Validation Set

（2）选择模型

• 在训练集上训练不同的模型
• 选择在验证集上错误最小的模型

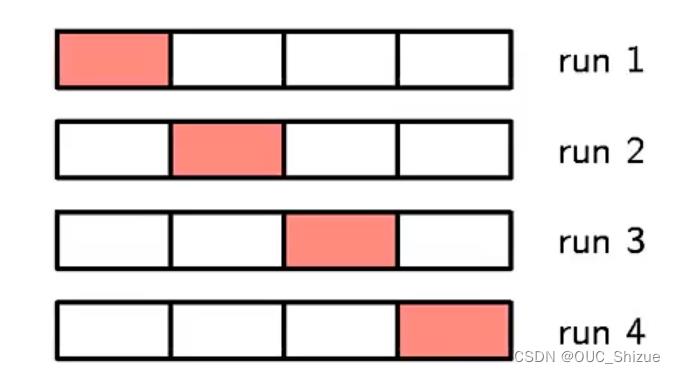
4、数据稀疏时进行交叉验证 Cross-Validation

• 将训练集分为S组，每次使用S-1组作为训练集，剩下一组作为验证集
• 取验证集上平均性能最好的一组

5、模型选择的准则

（1）一些准则

• 赤池信息量准则 Akaike Information Criterion，AIC
• 贝叶斯信息准则 Bayesian Information Criterion，BIC

（2）模型复杂度与期望风险之间的关系

• 偏差-方差分解 Bias-Variance Decomposition

6、偏差-方差分解

（1)期望风险

（2）机器学习能学到的最优模型

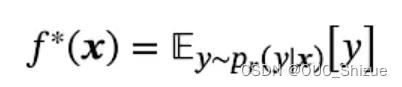
（3）期望风险分解

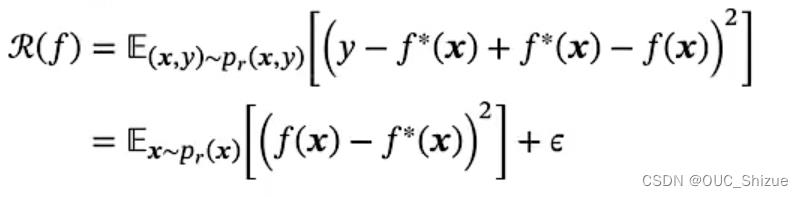
（4）具体方法

• bias.x：训练得到的所有模型的期望与最优模型期望的差值的平方，即该模型再不同数据集上得到的平均性能与最优性能的差值
• variance.x：在不同数据集上得到的期望与在所有数据集上的平均期望的差值，即该模型对每个数据集上的性能与平均性能之间的差值

（5）期望错误分解

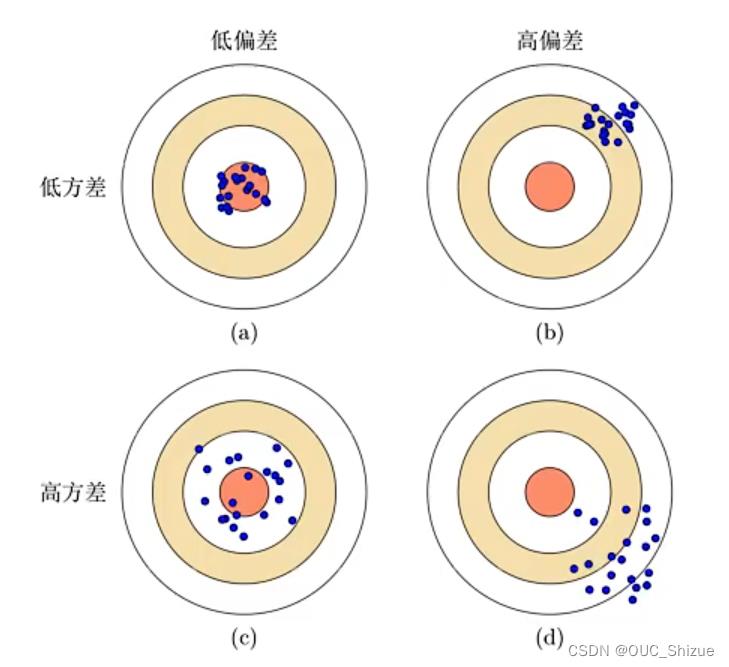
（6）偏差-方差评估模型好坏

​ 每个蓝点表示学习得到的一个模型，越靠近中心效果越好

• a表示理想模型
• b模型整体能力不够，欠拟合
• c模型整体能力不错，但整体较为分散，过拟合；一般通过模型集成来提高模型能力
• d模型为失败模型，避免出现

（7）bias、variance、模型复杂度三者关系

​ 注意最优模型并不位于bias与variance交点

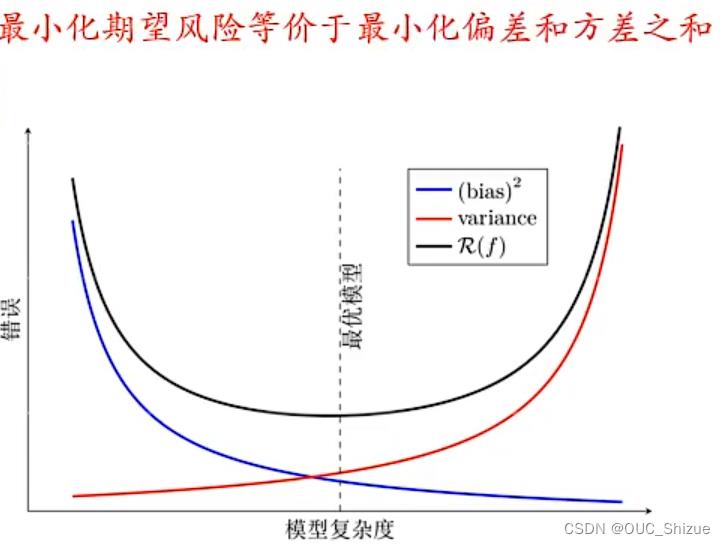
八、常用定理

1、没有免费午餐定理 No Free Lunch Theorem，NFL

​ 对于基于迭代的最优算法，不存在某种算法对所有问题都有效

2、丑小鸭定理 Ugly Ducking Theorem

​ 丑小鸭与天鹅之间的区别和两只天鹅之间的区别一样大

3、奥卡姆剃刀原理 Occam’s Razor

​ 如无需要，勿增实体；即可以用简单模型不用复杂模型

4、归纳偏置 Inductive Bias

​ 很多学习算法经常会对学习的问题做一些假设，这些假设就成为归纳偏执

• 最近邻分类器中，假设在特征空间中，一个小的局部区域中的大部分样本都同属一类
• 在朴素贝叶斯分类器中，我们会假设每个特征的条件概率是相互独立的
• 归纳偏置在贝叶斯学习中也常成为先验(Prior)

5、PAC学习

（1）定义

​ PAC: Probably Approximately Correct，根据大数定律，当训练集大小趋近无穷大时，泛化误差趋向于0，即经验风险趋近于期望风险

（2）样本复杂度计算

第二章：线性模型

一、分类问题示例

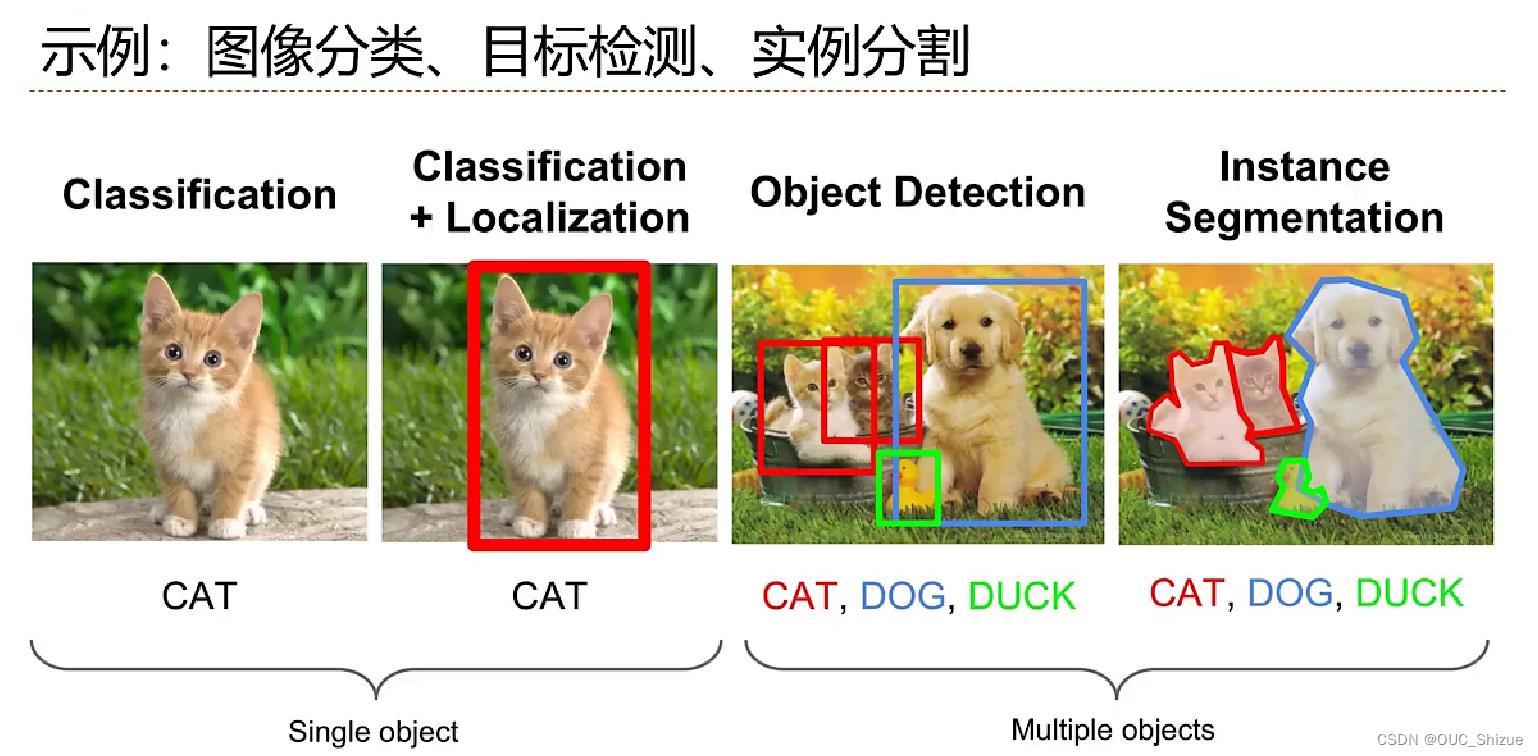
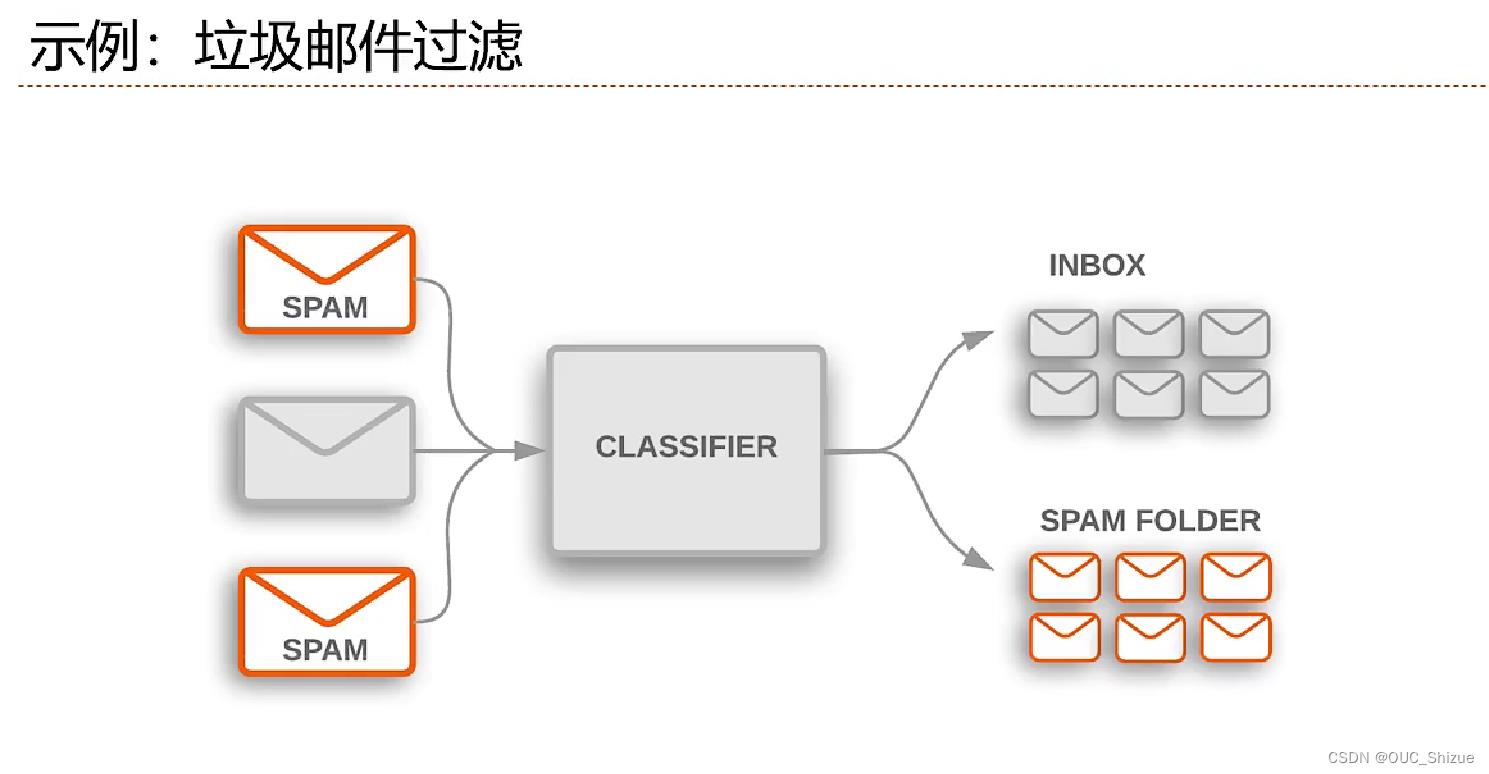
二、线性回归模型

1、线性回归模型

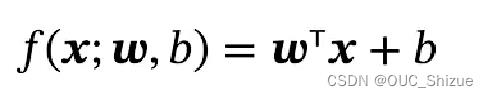
2、线性分类模型

• 由于x连续，而y为离散的label，因此可以在线性f外套一阈值函数，使其离散化。结果表示可以用0/1，+1/-1。
• 此处的f(x)也称为判别函数 Discriminant Function，g(x)为决策函数
• g(f(x;w))为离散模型，但目的是为了在面上画出分类线（或高维内的分类面），因此称为线性分类模型
• 线性分类模型=线性判别函数+线性决策边界

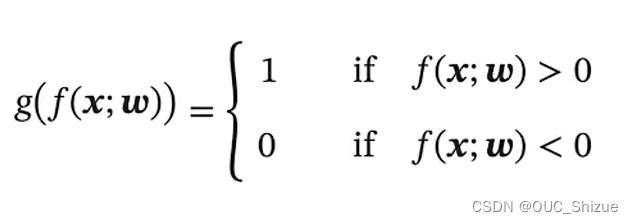
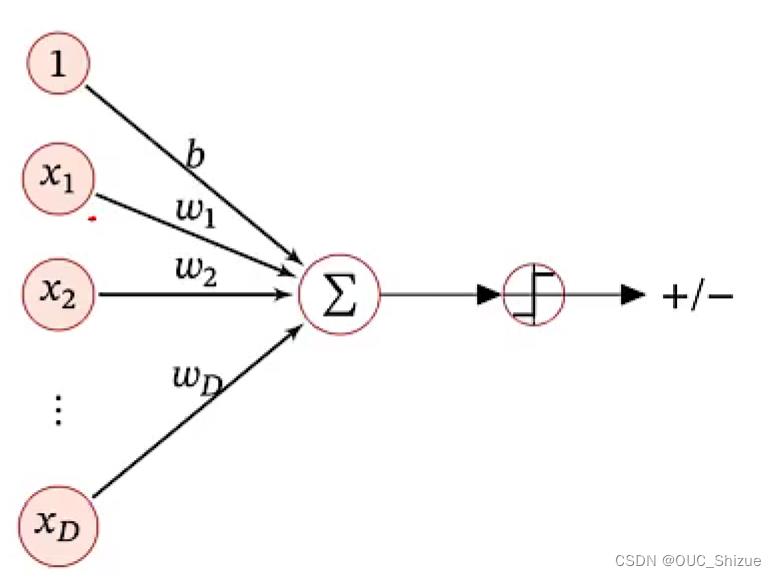
（1）二分类问题 Binary Classification

​ 学习准则/损失函数：0-1损失函数，即分类正确为1，分类错误为0，但由于该函数无法求导，因此无法对其进行优化

（2）多分类问题 Multi-class Classification

​ 一个超平面无法分解空间，因此需要多条线/面来分割空间；常见模型如下

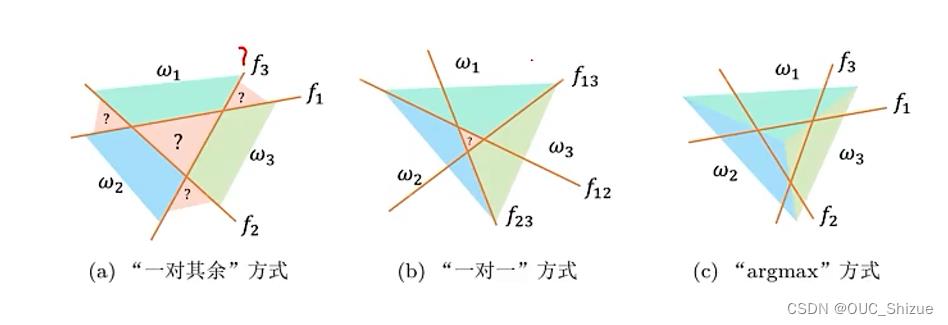
• a模型有多少个类就要建立多少个分类器，产生对应数量的决策面，接着投票；但是会存在问号所示的模糊区域，该类区域不属于任意一个类
• b模型两两建立分类器，即有C个类需要建立C(C-1)/2个分类器,但在C较大时所需要的分类器数量较多
• c模型对a进行改进，a模型为投票机制，因此会存在模糊区域；而c模型为按得分分类，每个点都属于其中一个类，简单理解为每个点属于其距离最近的类，从而消除了模糊区域

三、交叉熵与对数似然

1、信息论 Information Theory

2、自信息 Self Information

​ 一个随机事件所包含的信息量。对于一个随机变量X，当X=_x_时的自信息_I(x)定义为_I(x)=-log p(x),自信息具有可加性

3、熵 Entropy

（1）熵的信息论定义

​ 信息论中，熵用来衡量一个随机事件的不确定性，例如填词游戏中：applicatio_ 熵小于 appl_，一个事件一定发生则其信息量为0

• 熵越高，随机变量的信息越多
• 熵越低，随机变量的信息越少

（2）熵的数学定义

​ 随机变量X的自信息的数学期望称为熵,分布越均衡熵越大

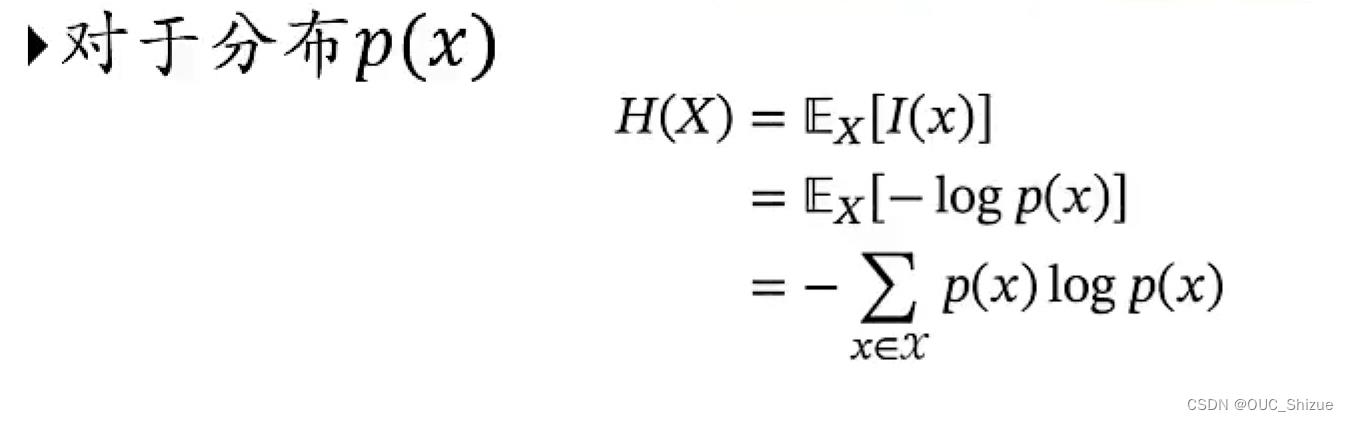
（3）熵编码 Entropy Encoding

​ 在对分布_p(y)_的符号进行编码时，熵_H§_也是理论上最优的平均编码长度，这种编码方式称为熵编码.

​ 例如对一篇文档中的a,b,c进行编码，可知其服从某一分布，可根据其自信息设置其码字长度：a的长度为_-log(a)，b的长度为-log(b)，c的长度为-log©，平均码字长度为_H§=-p(a)log(a)-p(b)log(b)-p©log©

（4）交叉熵 Cross Entropy

​ 可以利用交叉熵来衡量两个分布的差异

（5）KL散度 Kullback-Leibler Divergence

​ KL散度也可用于衡量两个分布的差异，差异越小KL散度越小，反之越大

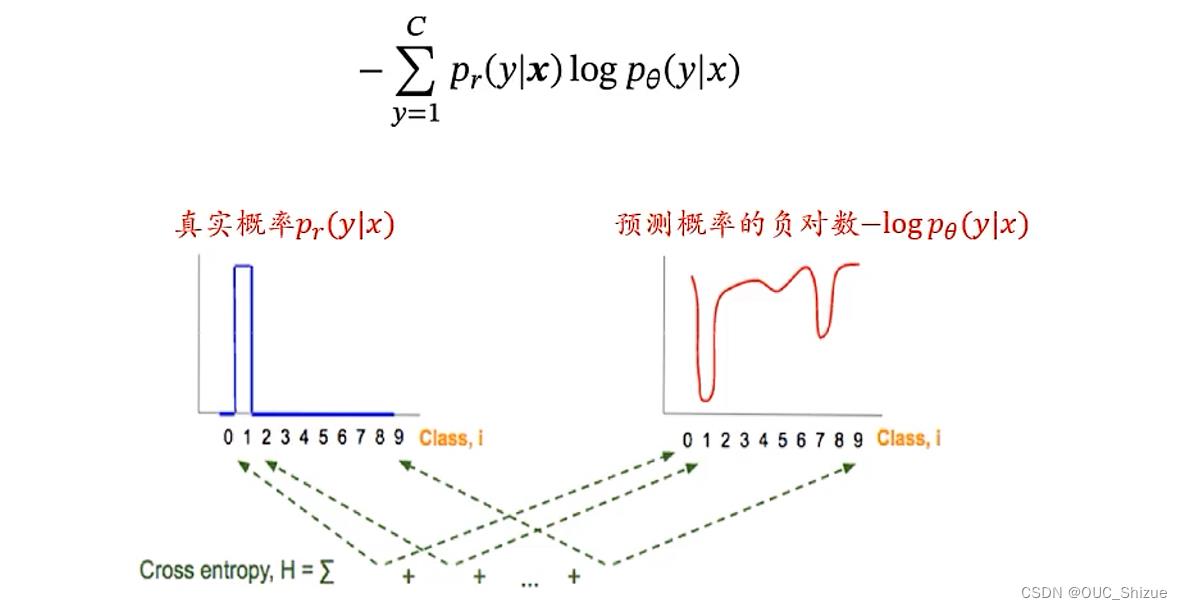
4、交叉熵与KL散度应用到机器学习

​ 可以用于衡量真是分布与预测分布之间的差异

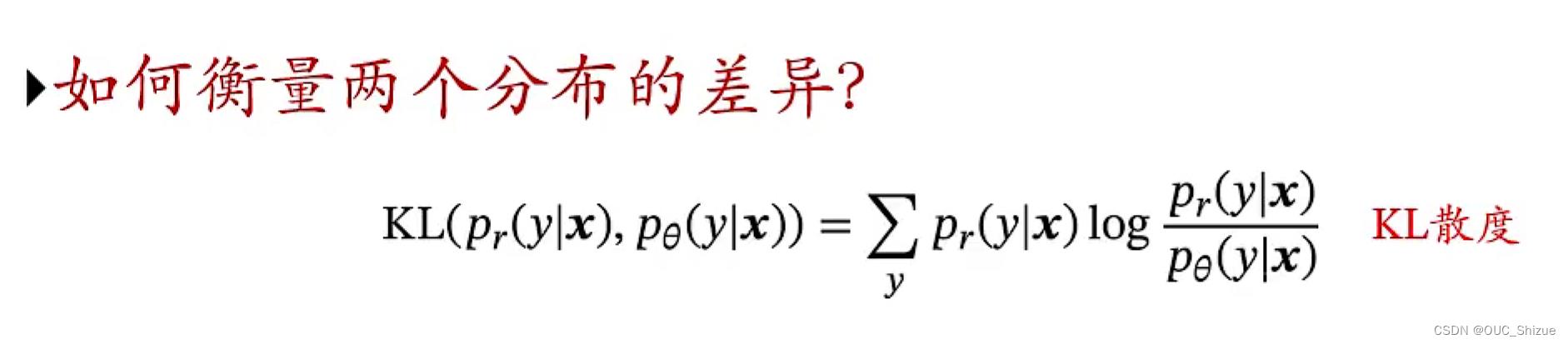
​ 由于优化的部分为Pθ，即预测分布，与真实分布Pr无关，因此上式可简化为

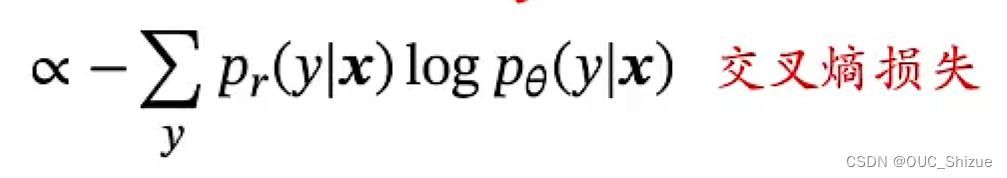
​ 因此最小化两个分布的差异，即最小化两个分布的交叉熵；而式中的Pr为one-hot向量形式，因此除_y*项之外均为0，因此可写为_min KL=-logpθ(y*|x)，即负对数似然，因此优化目标转化为使对数似然最大化，即最大对数似然估计

四、Logistic回归 Logistic Regression

1、模型

​ 也称为对数几率回归，简称对率回归，模型如下，其中1为增广向量：

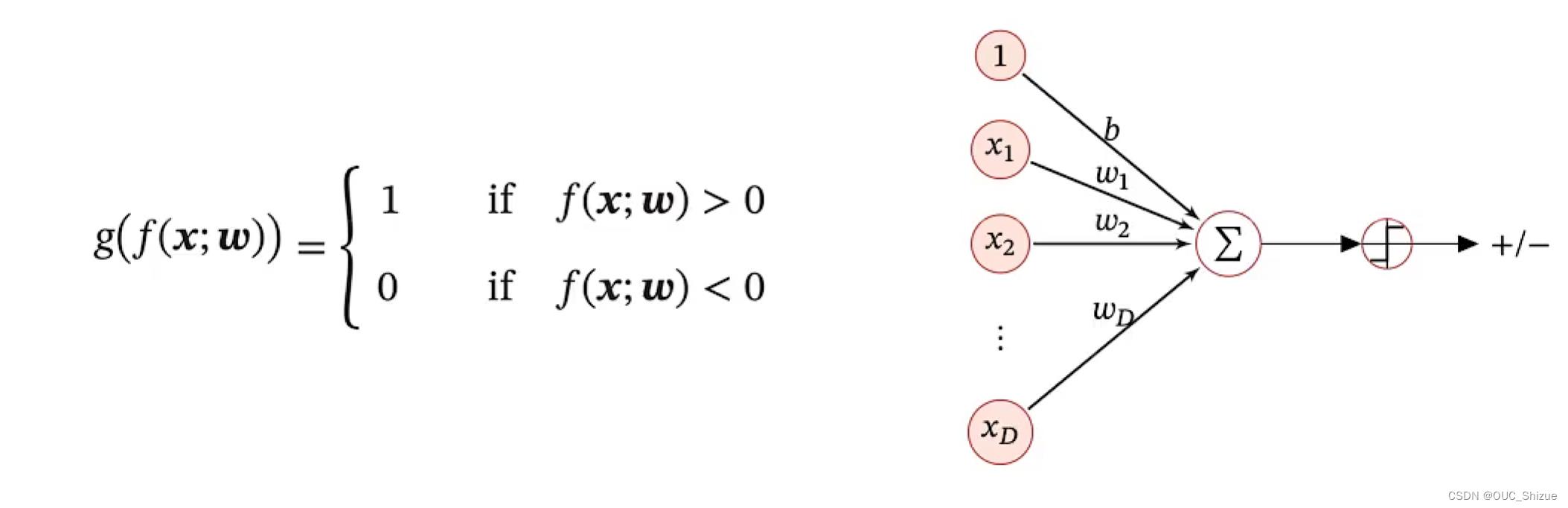
2、分类问题

3、Logistic函数

​ 此类函数也称为Sigmoid函数，其单增且反函数单增，两端饱和，因此常用作神经网络的激活函数，即上述函数g

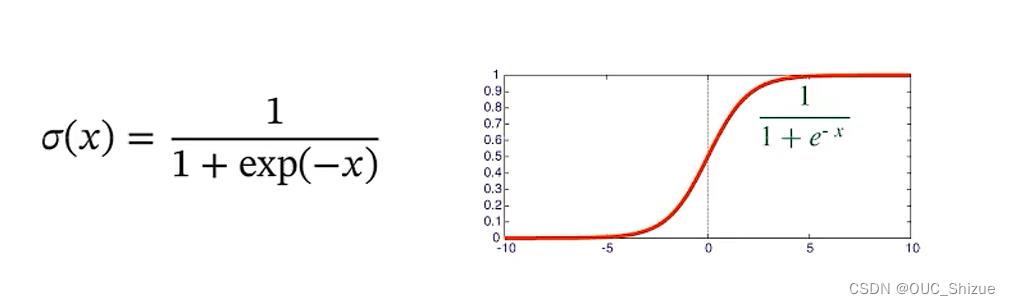
4、Logistic回归

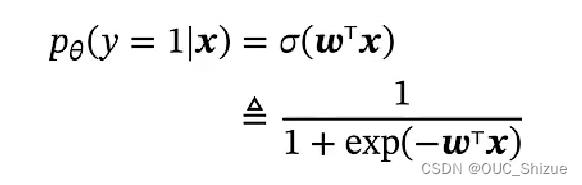
5、损失函数（学习准则）

​ 由于Logistic回归函数不可导，因此需要将损失函数转化到交叉熵模块，从而进行优化。

（1）定义

（2）梯度下降

五、Softmax回归

​ Softmax回归可以理解为Logistic回归在多分类问题上的扩展

1、多分类问题 Multi-class Classification

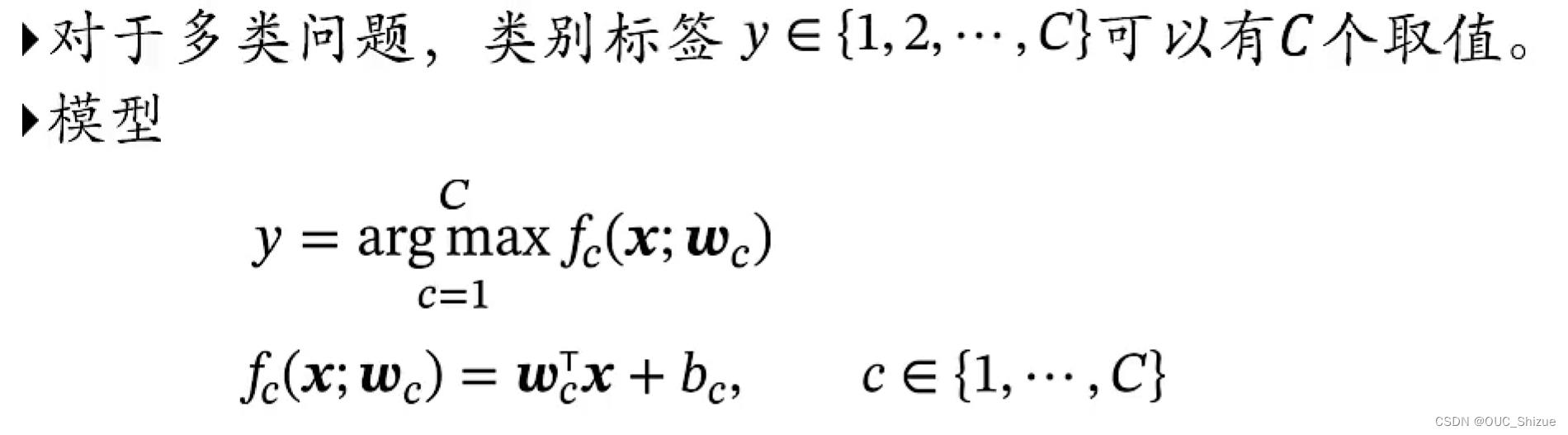
2、Softmax函数

​ 例如：

3、Softmax回归

4、交叉熵损失

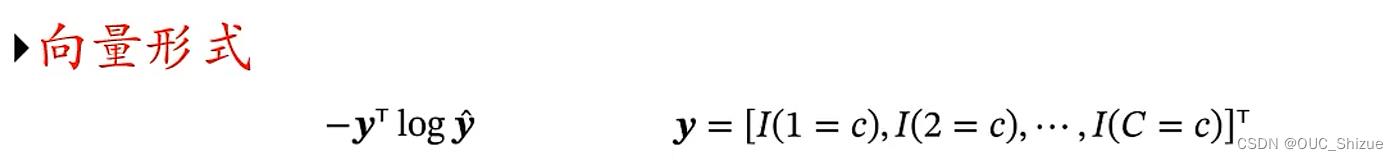
​ 例子：

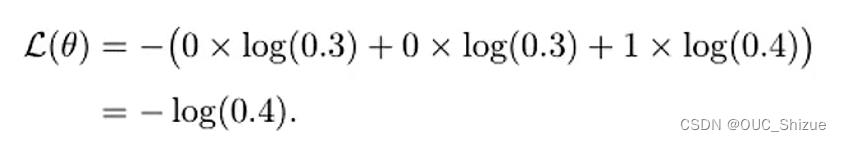
5、学习准则：交叉熵

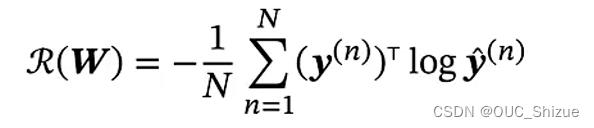
六、感知器

1、模型

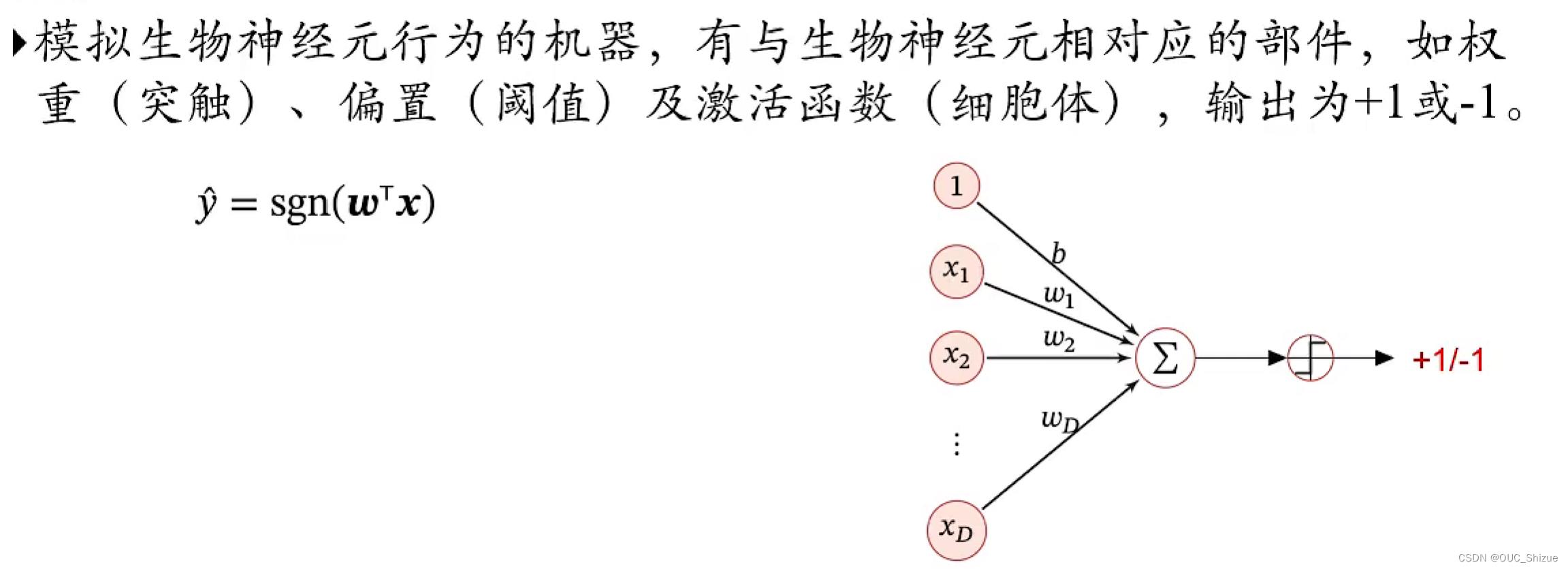
​ 在感知器中y(n)取+1/-1，当y(n)=+1时，如果上式小于0，这说明w*Tx(n)<0，即预测结果为-1，说明预测错误，反之如果上式>0成立则说明预测正确

2、学习算法

​ 每次更新w以后ywTx的值较原值增大，每次更新一个样本，直到所有样本分类正确

3、学习准则

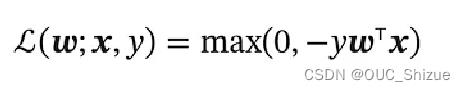
​ 当分类正确时，梯度为0，分类错误时，梯度为-yx

4、感知器的学习过程

​ 每次循环需要对样本重新随机排序，否则靠后的样本对模型的影响会较大，需要进行正则化增大随机性；迭代次数也可通过设置验证集，当模型在验证集上的错误率不再下降时停止迭代。

​ 下图为感知器参数学习的更新迭代过程，分界面为WTx=0：

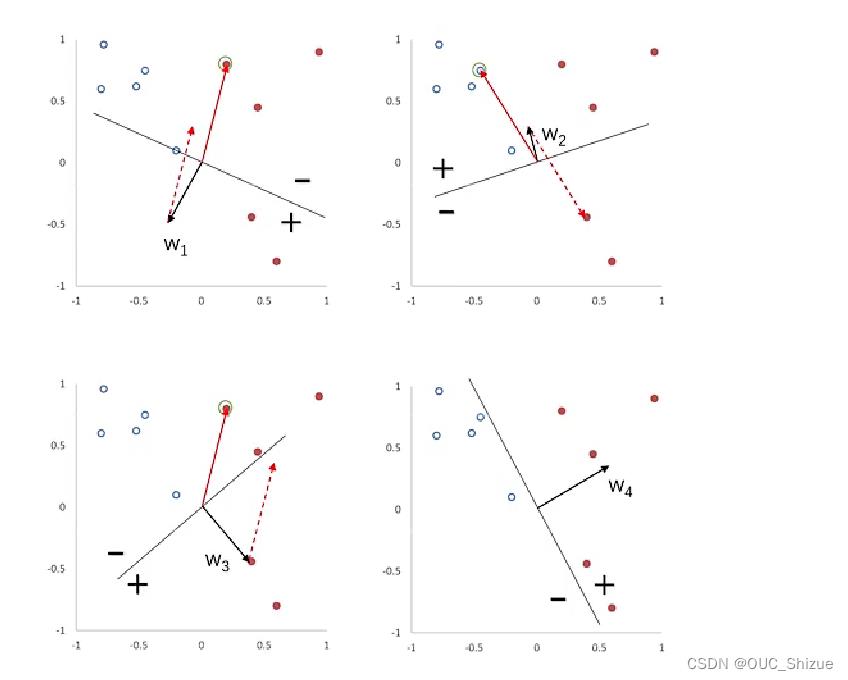
5、收敛性

七、支持向量机 Support Vector Machine

1、最大间隔

2、支持向量机 SVM

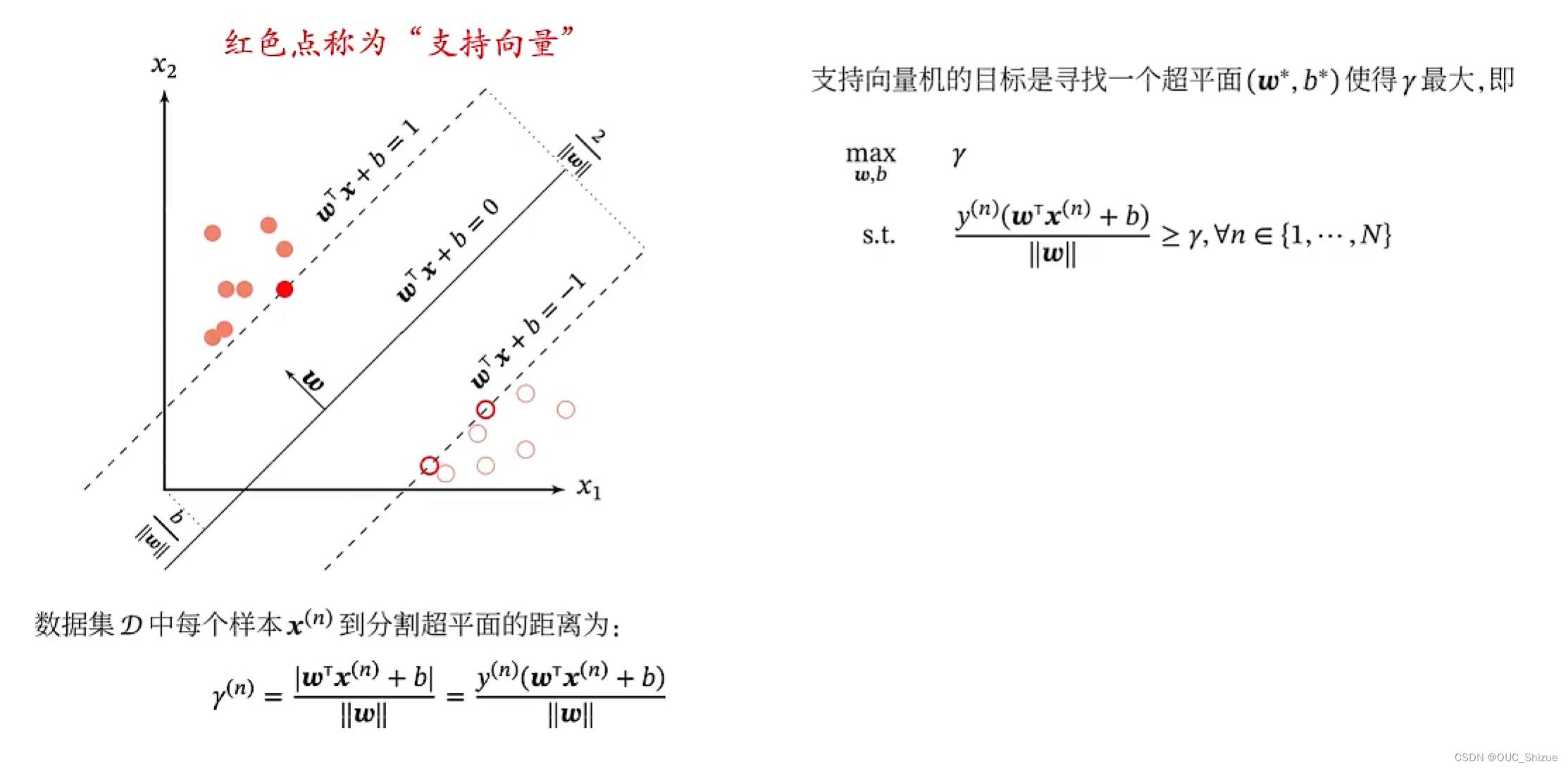
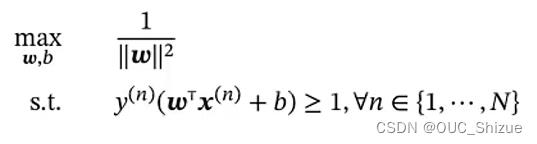
3、软间隔 Soft Margin

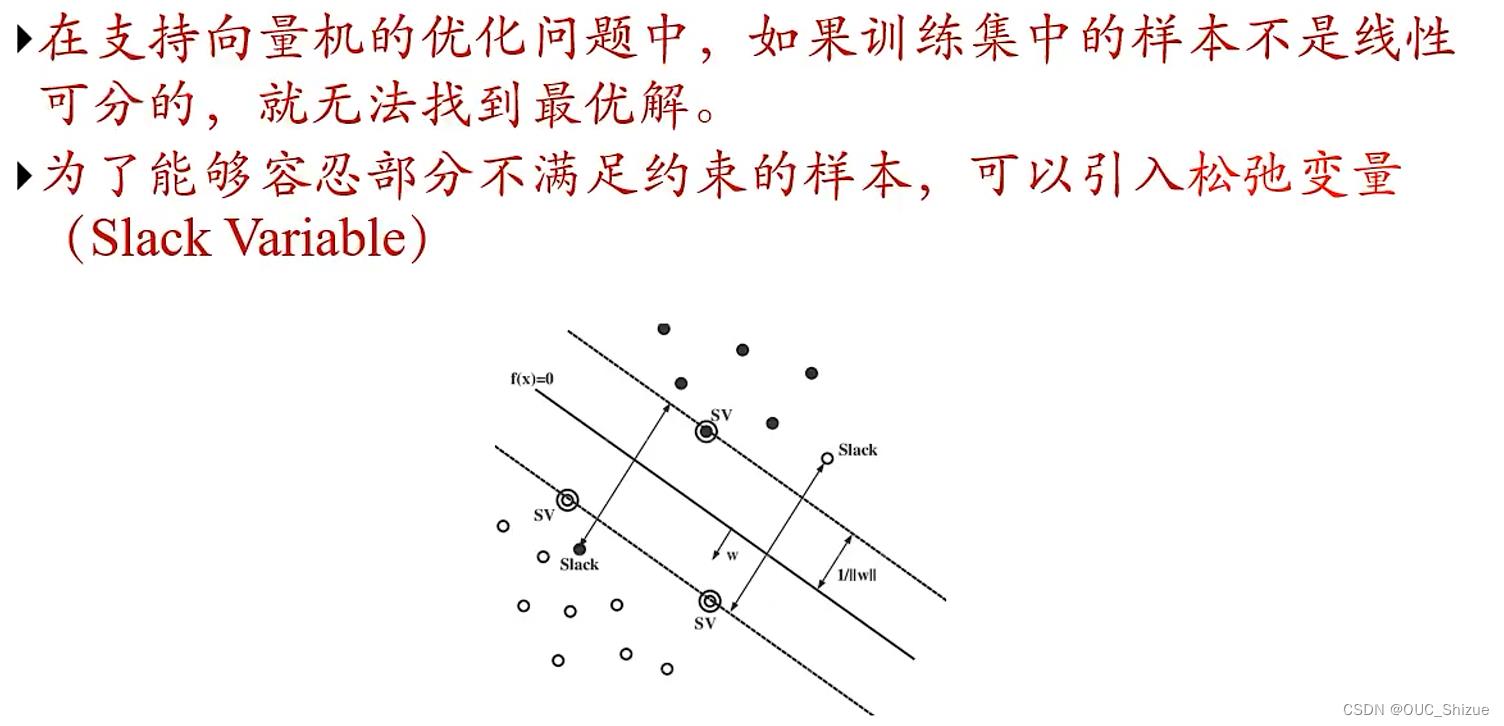
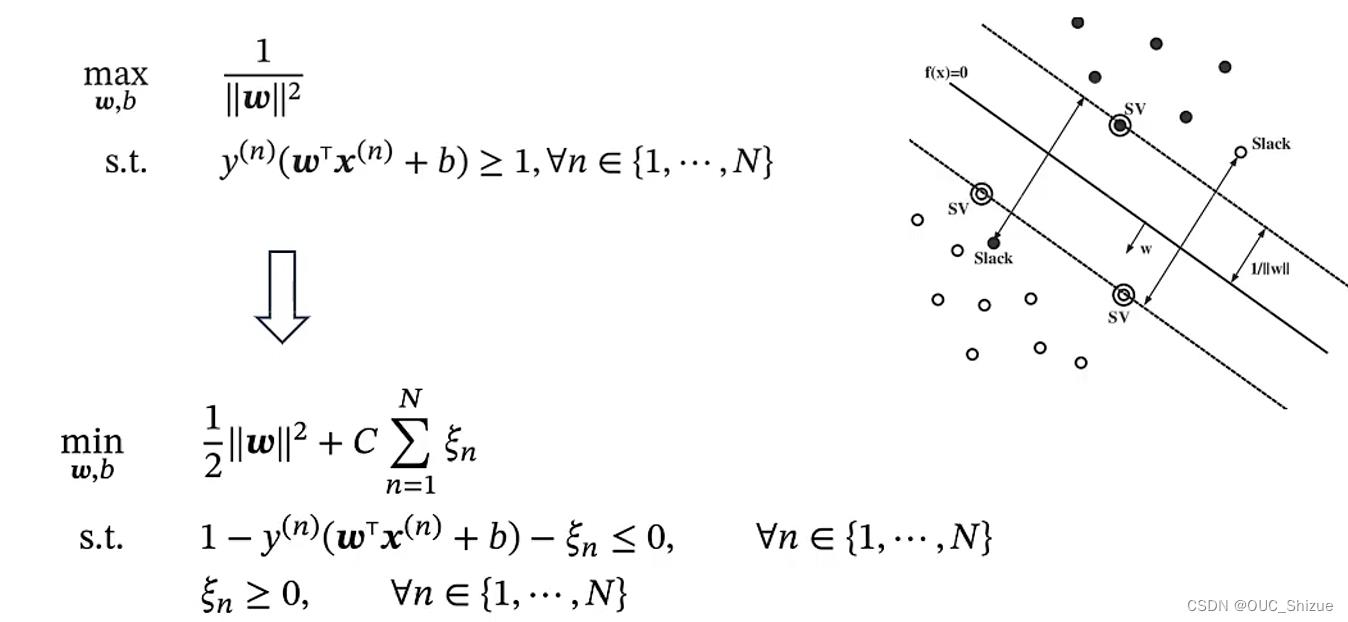
​ 如果ξ=0则样本线性可分，0<ξ<1说明模型可以分对，但存在部分样本不可分；ξ>1则说明会出现分类错误；因此软间隔SVM的目标为ξ最小

4、带软间隔的支持向量机

​ 可以理解为max部分为经验风险，后项为正则化项，该式也称为Hinge损失函数，感知器损失如下：

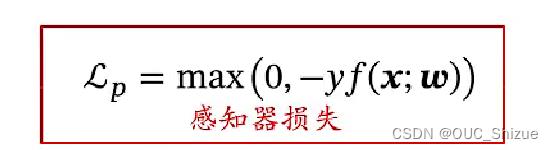
​ 对比可见感知器内的点只要分对就不做惩罚，而SVM中即使分对但margin<1仍然要做惩罚

5、SVM优化

• 约束优化问题，可用拉格朗日优化/KKT算法，可将约束优化转化为非约束优化
• SMO算法
• 梯度下降法

6、SVM优势

​ 可以和核方法（Kernel Method）相结合

八、线性分类模型总结

1、不同损失函数的对比

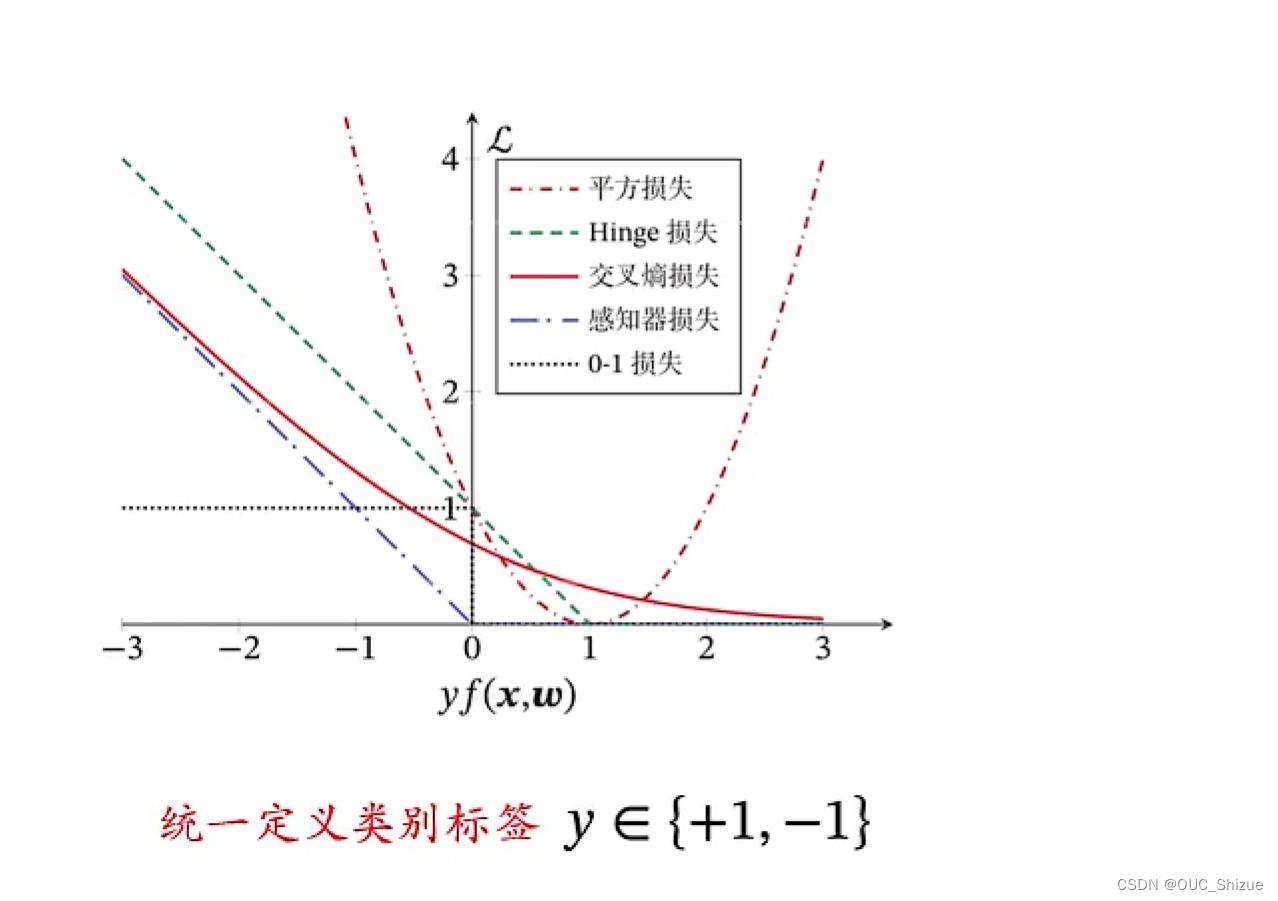
（1）平方损失

​ 从图中可见平方损失在x=1之后上升，说明预测正确依然进行了惩罚，因此平方损失不适合用于分类任务

（2）Logistic回归

​ 随着f(x)的增大对应损失越来越小，符合客观认知，但在f(x)=1之后仍然进行了惩罚，对于分类任务是没有必要的，因此需要再次优化

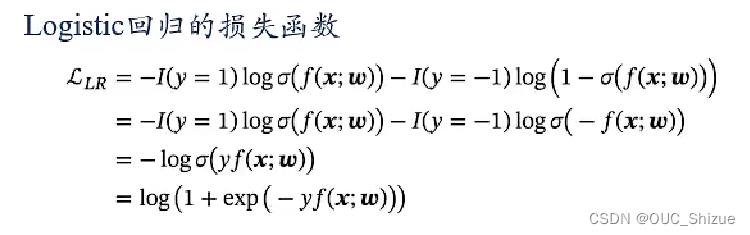
（3）感知器损失

​ 只要小于0就惩罚，因此适合用感知器进行分类

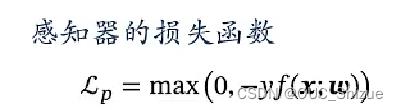
（4）软间隔SVM损失/Hinge损失

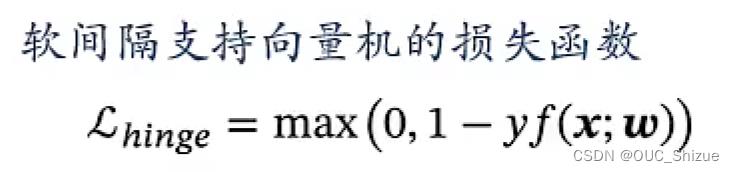
​ 直观理解为感知器向右平移了一个单位，这一个单位用于宽容边界值，小于边界值才进行惩罚

2、小结

3、线性不可分：XOR问题的解决

(1)问题描述

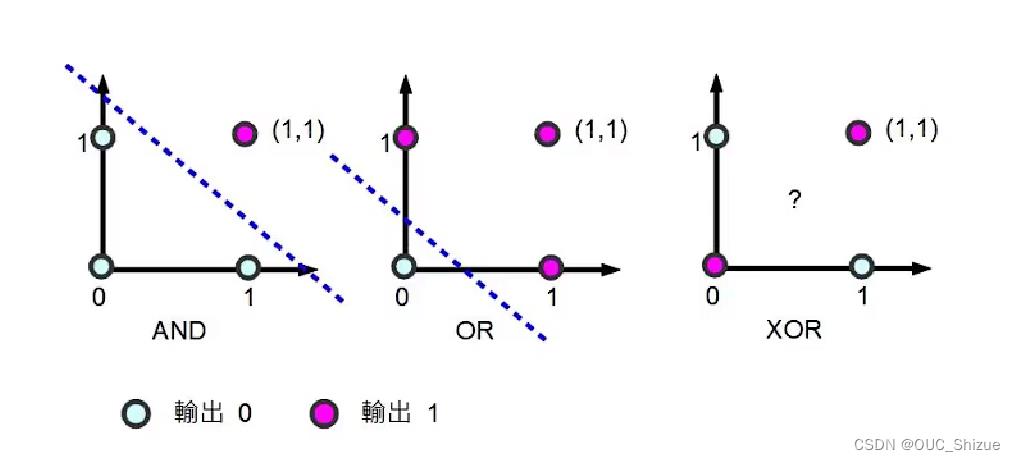
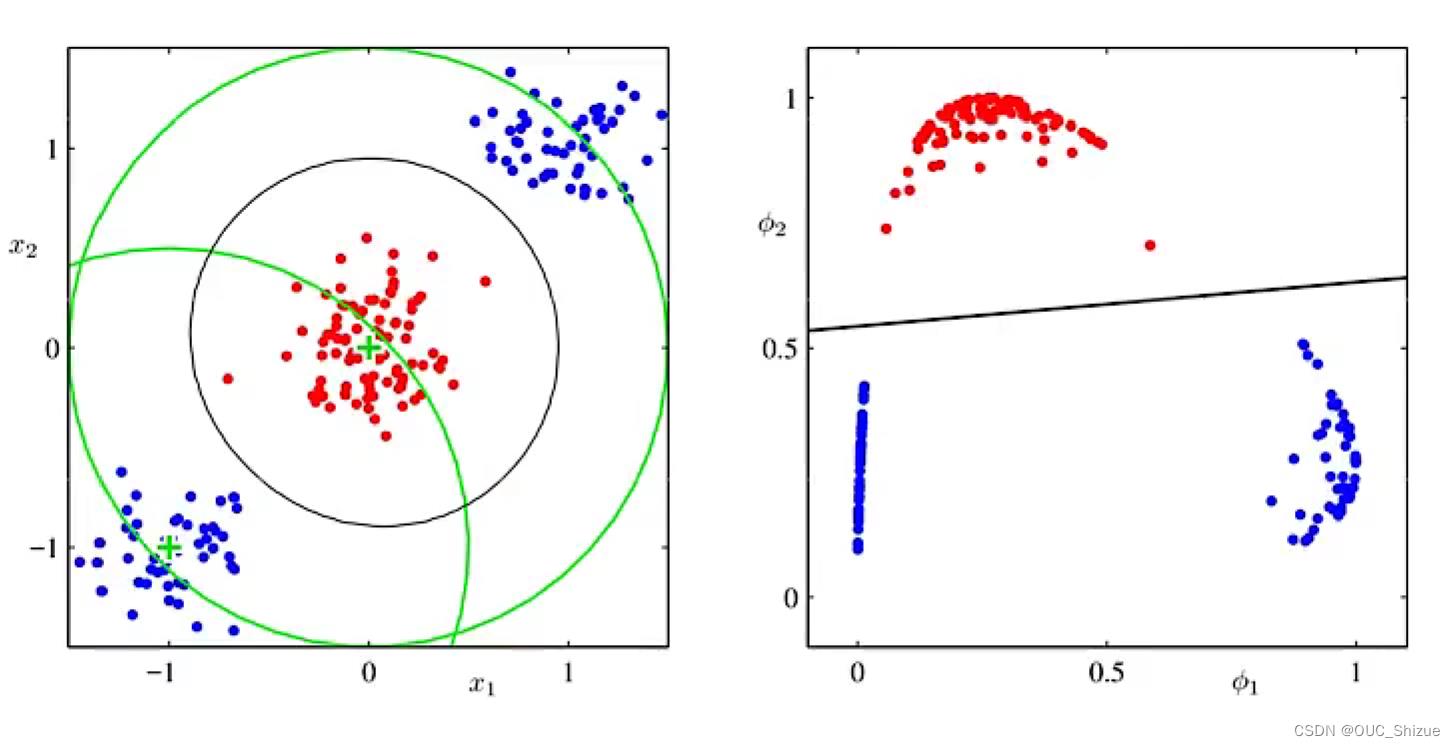
（2）解决方法：使用“基函数”的广义线性模型

​ 例如使用图中一个点作为锚点，然后构造φ(x)计算每个点距离锚点的距离，将两部分点在新的空间构造，从而在新的平面内线性可分

第三章：前馈神经网络（全连接神经网络） FNN

一、神经元

1、激活函数性质

• 连续并可导（允许少数点上不可导）的非线性函数：可导的激活函数可以直接利用数值优化的方法来学习网络参数
• 激活函数及其导数要尽可能简单，有利于提高网络计算的效率
• 激活函数的导函数的值域要在一个合适的区间内，不能太大也不能太小，否则会影响训练的效率及稳定性
• 总体上升，部分区域可以有波动

2、常用的激活函数

（1）S型函数

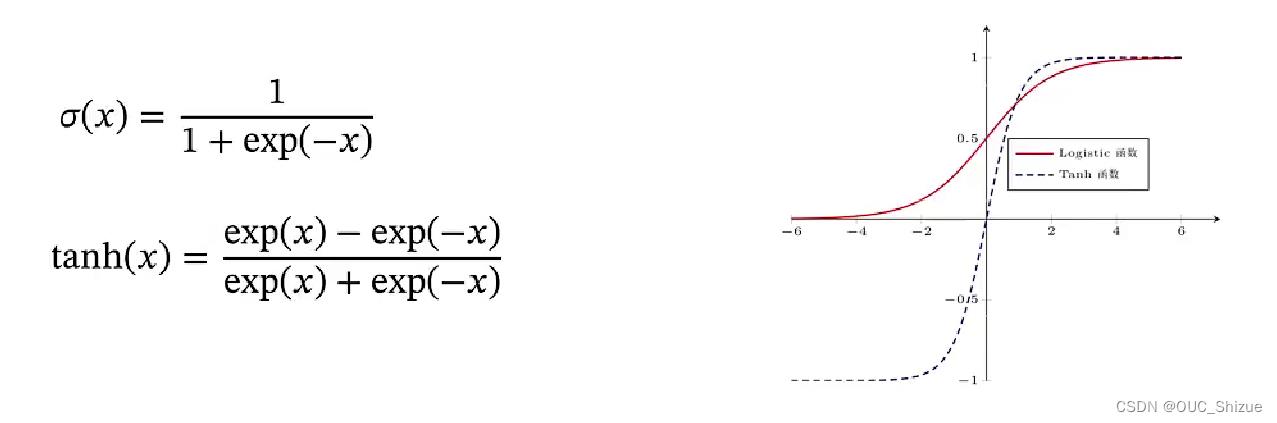
• 相互转化:tanh(x)=2σ(2x)-1
• 都是饱和函数
• Tanh函数是零中心化的，而Logistic函数的输出恒大于0
• 非零中心化的输出会使得其后一层的神经元的输入发生偏置偏移(bias shift)，并进一步使得梯度下降的收敛速度变慢；消除方法为对数据进行归一化；或者加上一个偏置σ(x)+b

（2）斜坡函数

Relu函数

​ 当前机器学习激活函数首选Relu函数，但是存在死亡Relu问题(Dying Relu Problem)，由于ReLU函数左侧为0，因此会出现所有输出都为0的绝对抑制状态，改进方法为使用LeakyReLU(x)函数，即在函数左边让其等于一个很小的参数，从而有了一个小的梯度，保证参数可以更新

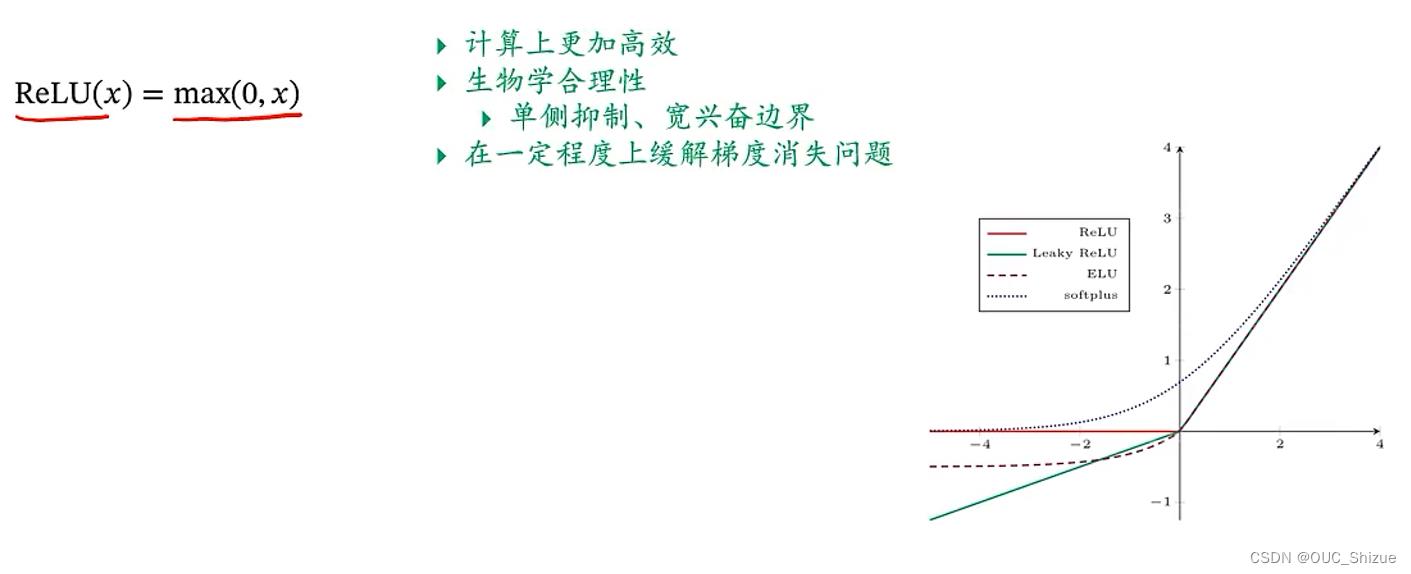
LeakyReLU函数

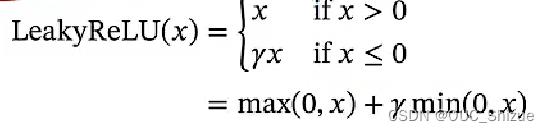
​ 如绿线所示，在x<0时也有一个较小梯度，可以让模型慢慢更新

近似的零中心化非线性函数

Rectifier函数的平滑版本

​ 用曲线去逼近ReLU函数，但是计算相较于ReLU函数复杂，首选仍然是ReLU

​ Softplus(x)=log(1+exp(x))

（3）复合函数

（1）Swish函数：一种自门控(Self-Gated)激活函数

​ 可以理解为Logistic函数与斜坡函数复合

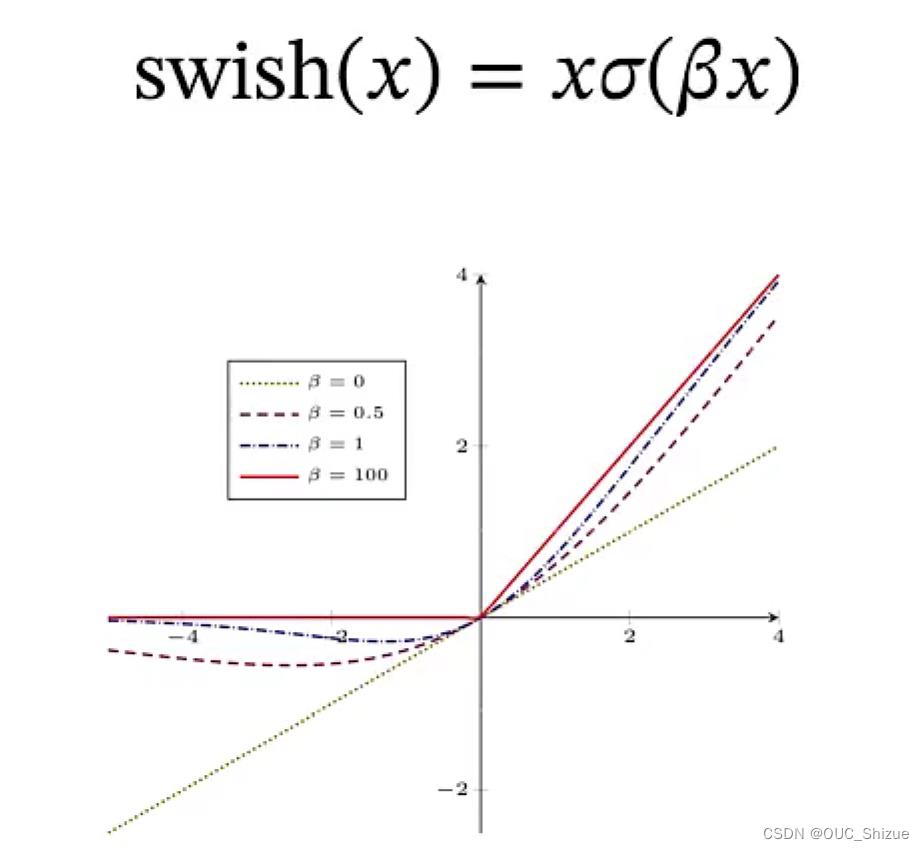
（2）高斯误差线性单元 Gaussian Error Linear Unit，GELU

​ 高斯分布的累积分布函数也是S形函数，与swish函数类似；但由与高斯分布没有解析解，因此无法直接得到GELU函数，但可以通过Logistic函数与Tanh函数来近似。

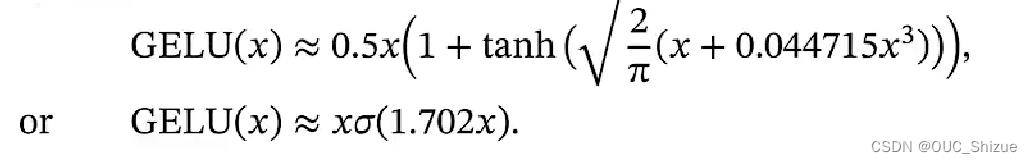
3、几种激活函数总结

二、神经网络

1、神经网络三个组成

（1）神经元的激活规则

​ 主要指神经元输入到输出之间的映射关系，一般为非线性函数。

（2）网络的拓扑结构

​ 不同神经元之间的连接关系

（3）学习算法

​ 通过训练数据来学习神经网络的参数

2、连接主义模型

三、前馈神经网络

1、基础概念

• 各神经元分别属于不同的层，层内无连接
• 相邻两层之间的神经元全部两两连接
• 整个网络中无反馈，信号从输入层向输出层单向传播，可用一个有向无环图表示

​ 神经网络中输入层为第0层，后续以次为1、2、3…层，其中L M f为超参数，W b为参数，z a为活性值

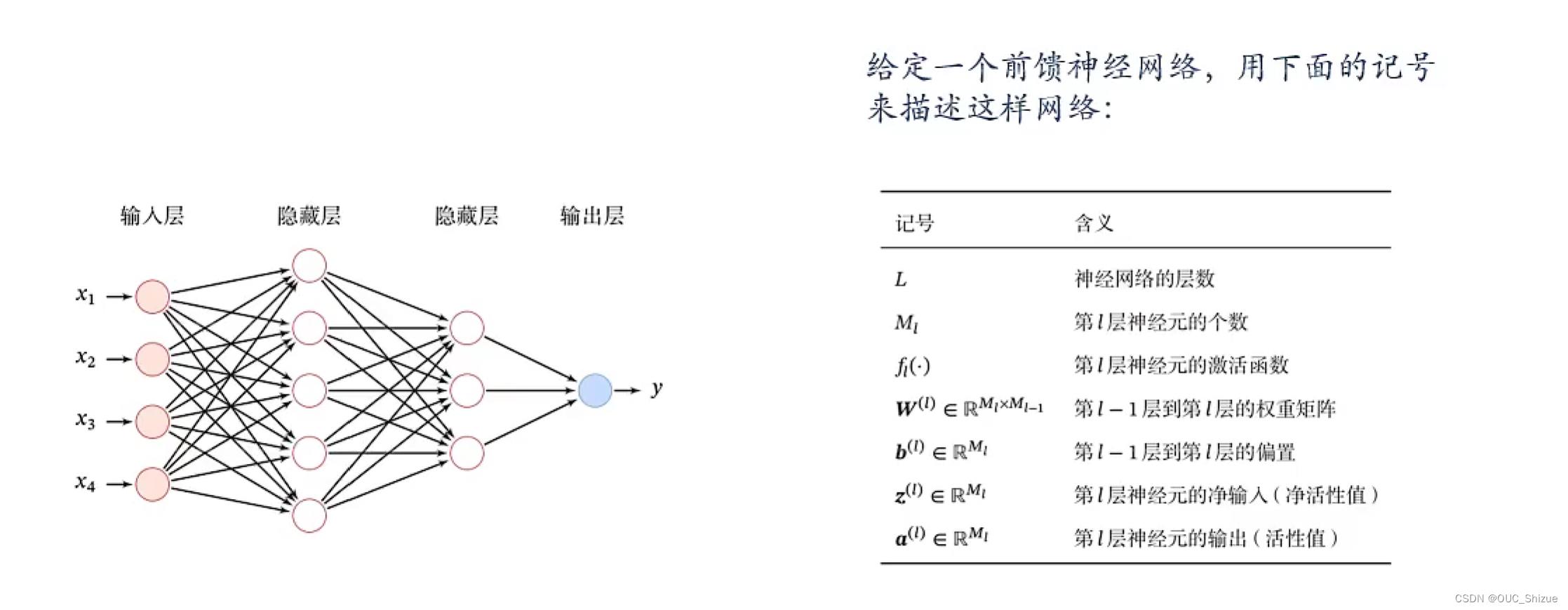
2、信息传递过程

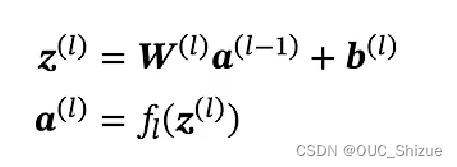
​ 合并后得到：

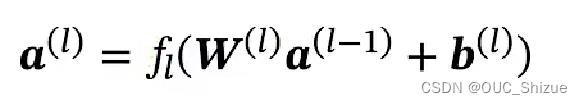
​ 前馈计算：

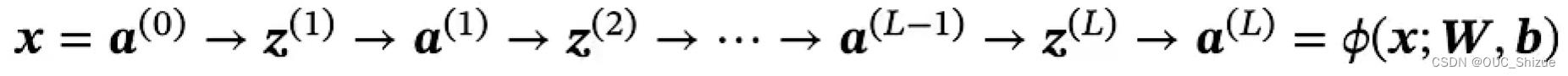
3、通用近似定理

4、应用到机器学习

​ 如果g()为Logistic回归，那么Logistic分类器可看做神经网络的最后一层

5、参数学习

（1）对于多分类问题

（2）结构化风险函数

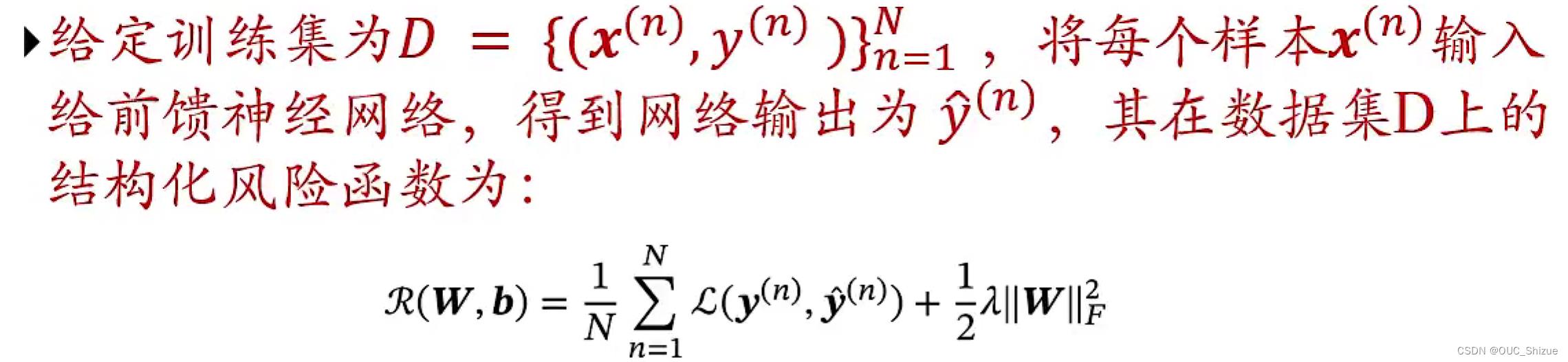
​ 其中正则化项可以选择Frobenius范数

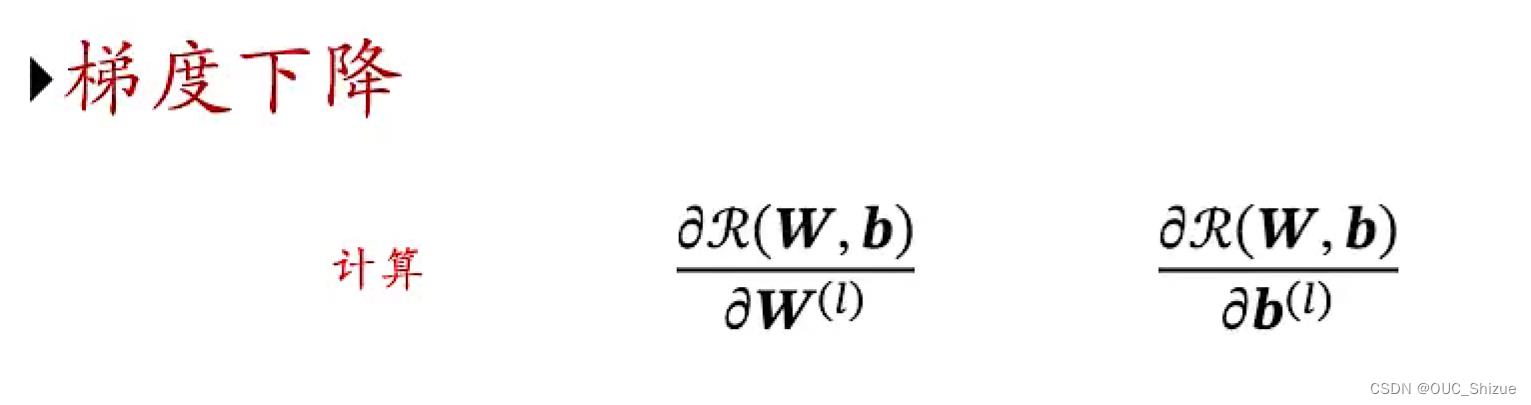
6、梯度计算方法

​ 神经网络是一个复杂的复合函数，有以下求解方法：

• 链式法则求解
• 反向传播算法（根据前馈网络的特点而设计的高效方法）
• 自动微分 Automatic Differentiation，AD

四、反向传播算法

1、定义

​ 反向传播(Backpropagation，BP）是误差反向传播的简称，是一种与最优化方法（如梯度下降法）结合使用的，用来训练人工神经网络的常见方法。 该方法对网络中所有权重计算损失函数的梯度。 这个梯度会反馈给最优化方法，用来更新权值以最小化损失函数。

2、算法实现

3、实例

（1）网络图

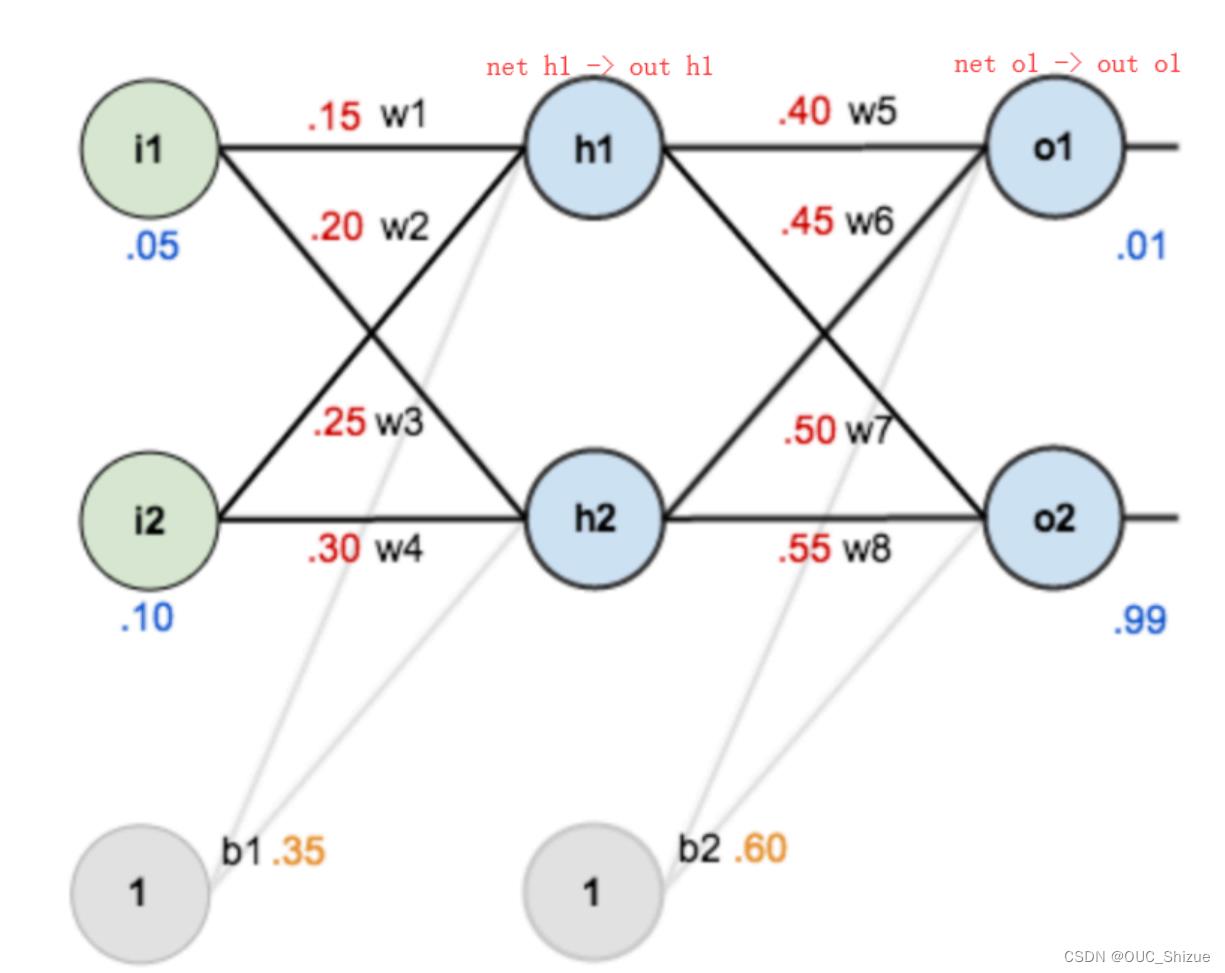
（2）前馈运算 激活函数为sigmoid

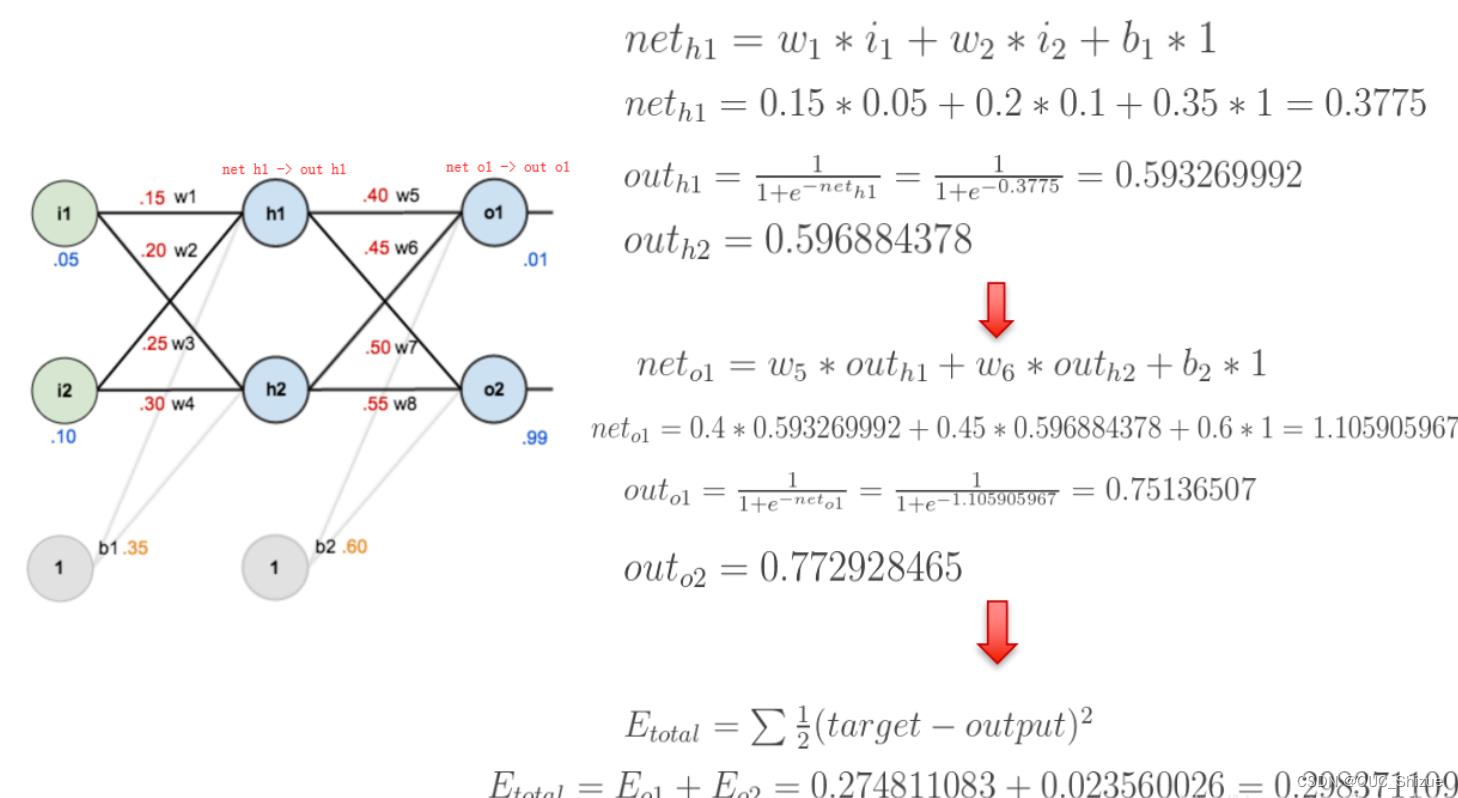
（3）反向传播

（4）参数更新

五、计算图与自动微分

1、定义

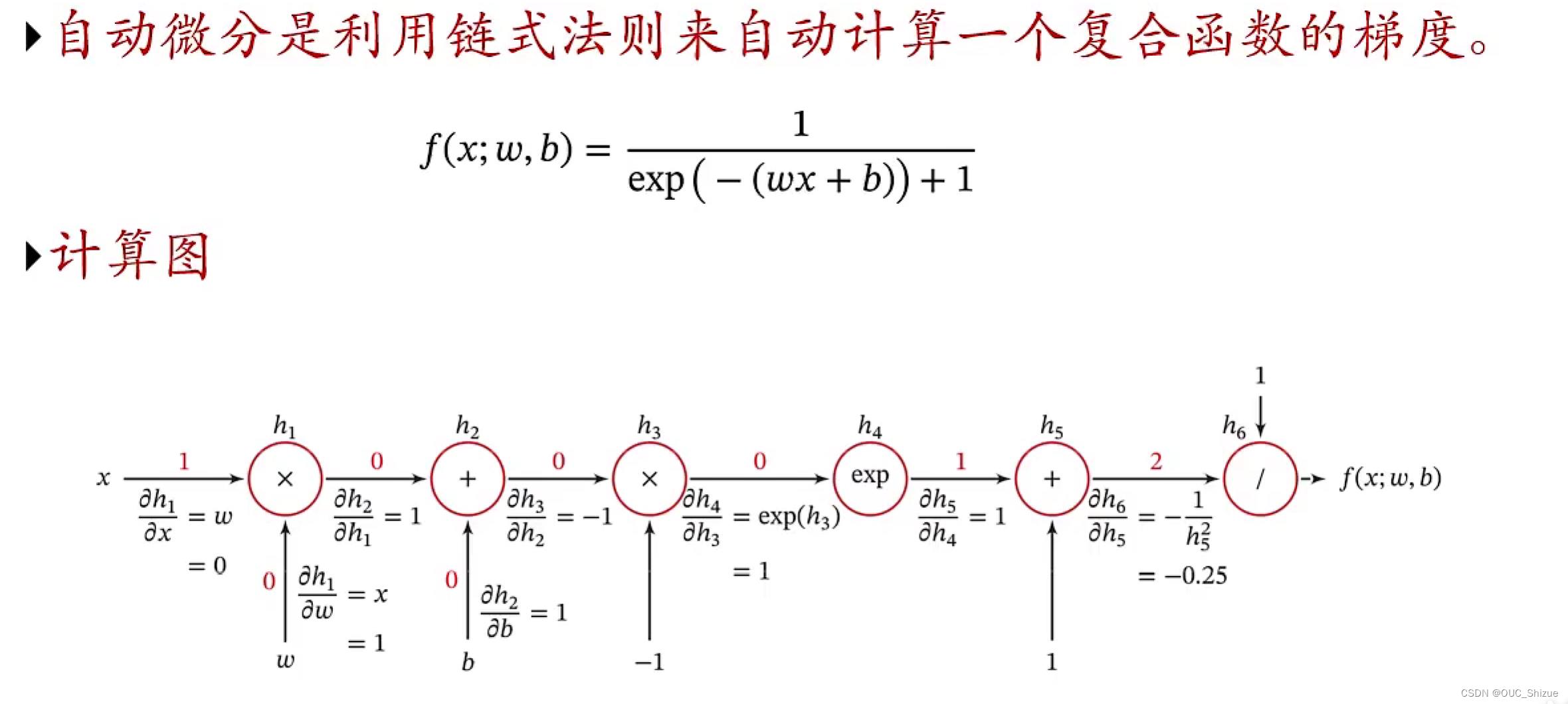
2、实例

​ 针对上图有：

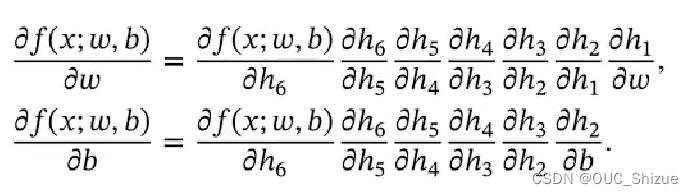
​ 当x=1，w=0，b=0时，可以得到：

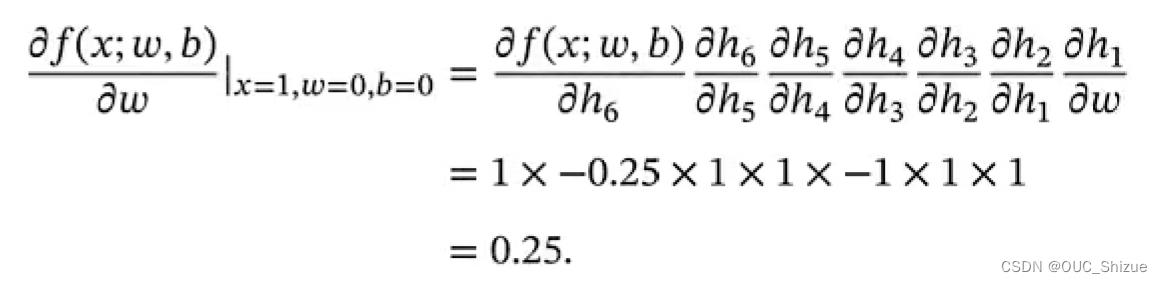
3、前向模式与反向模式

• 前向模式：传递过程中保存的参数较多，资源消耗可能过大
• 反向模式：与反向传播相同，资源占用较少

4、静态计算图和动态计算图

• 静态计算图是在编译时构建计算图，计算图构建成功之后在运行时不能改变，效率较高，可以在构建时进行优化，并行能力强，但灵活性较差（Theano、TensorFlow）
• 动态计算图在程序运行时动态构建，不容易进行优化，且输入的网络结构不一致时难以进行并行计算，但灵活性较高（DyNet、Chainer、Pytorch）

5、Keras快速搭建神经网络

6、深度学习的三个步骤

• 定义网络
• 损失函数
• 优化

六、前馈神经网络优化

1、非凸优化问题

​ 局部最优但不是全局最优

2、梯度消失问题 Vanishing Gradient Problem

​ 例如导数在0~1之间，连乘以后梯度趋近于0，导致梯度消失，当神经网络深度较深时，下层网络的梯度趋近于0，难以更新；因此激活函数的导数最好在1附近，不能太大或过小，故推荐ReLU函数

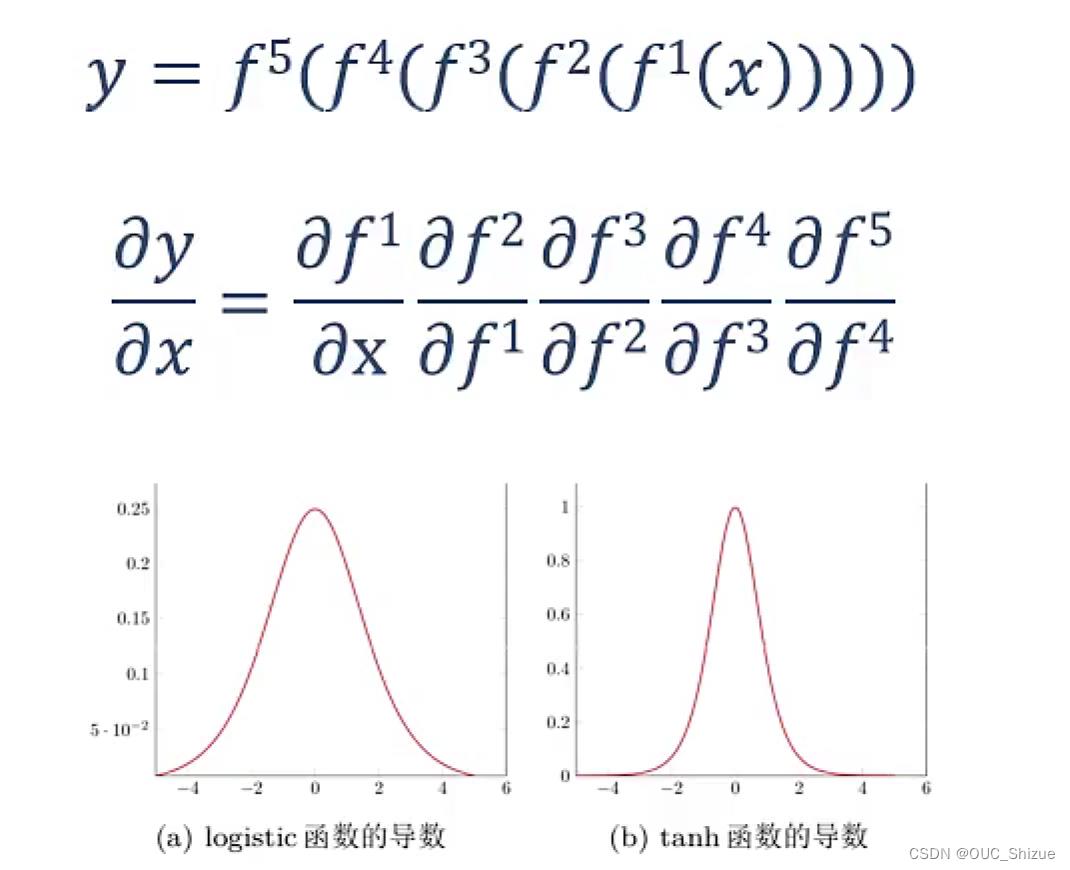
3、优化问题难点

• 非凸优化问题：存在局部最优而非全局最优解，影响迭代
• 梯度消失问题：下层参数比较难调
• 参数过多，影响训练，参数解释起来比较困难

4、优化问题需求

• 计算资源要大
• 数据要多
• 算法效率要好，收敛速度快

第四章：卷积神经网络 CNN

一、概述

1、卷积神经网络 Convolutional Neural Networks，CNN

• 前馈神经网络的一种
• 受生物学上感受野（Receptive Field）的机制而提出，在视觉神经系统中，一个神经元的感受野是指视网膜上的特定区域，只有这个区域内的刺激才能激活该神经元

2、CNN的三个结构特性

• 局部连接
• 权重共享，降低参数数量
• 空间或时间上的次采样

二、卷积

1、定义

w被称为滤波器（filter）或卷积核（convolution kernel）

​ 如果输入长度为N，滤波器长度为K，则output长度为N-K+1

2、举例

​ 此处选用Filter:[-1,0,1]

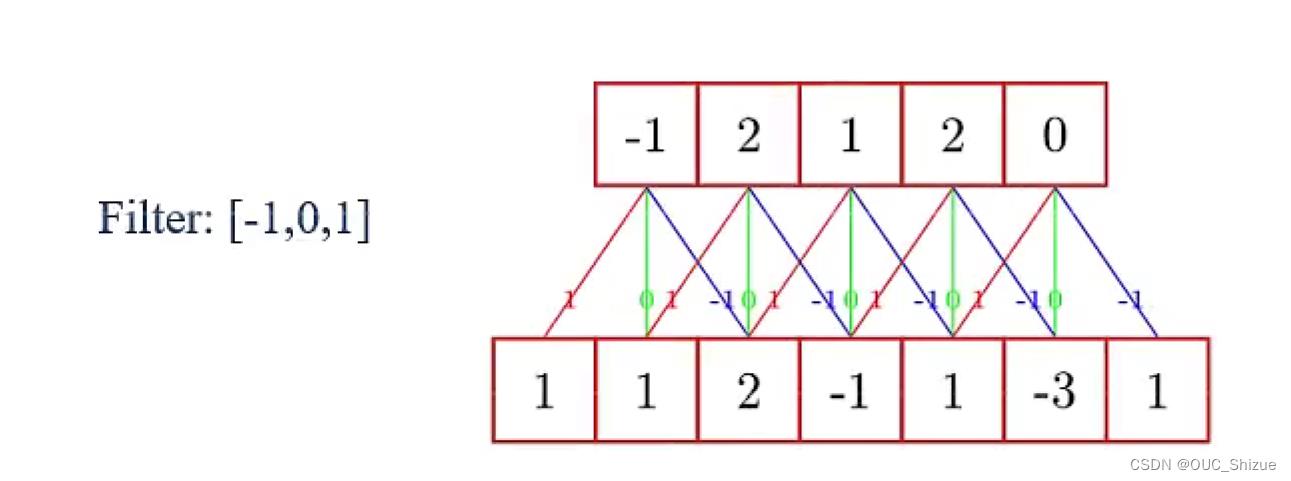
3、卷积的作用

（1）近似微分

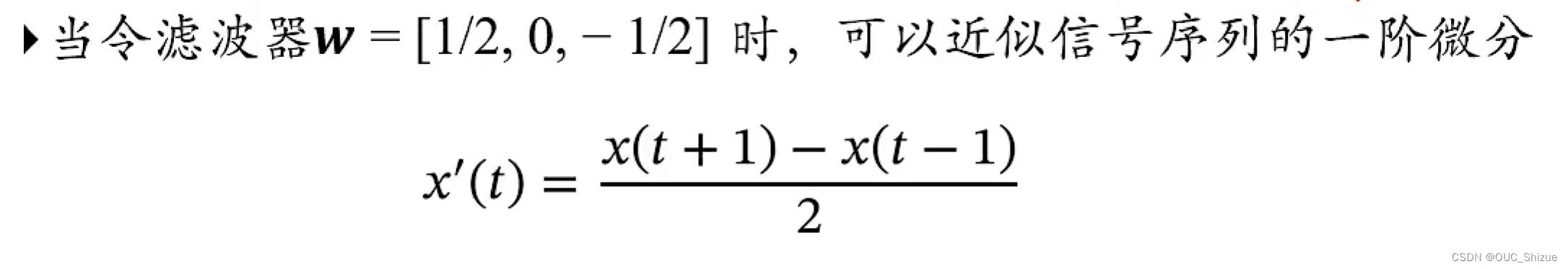
​ 同理，当滤波器w=[1,-2,1]时，可以近似信号序列的二阶微分

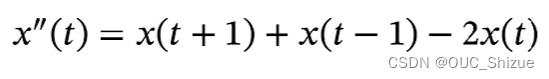
（2）低通滤波/高通滤波

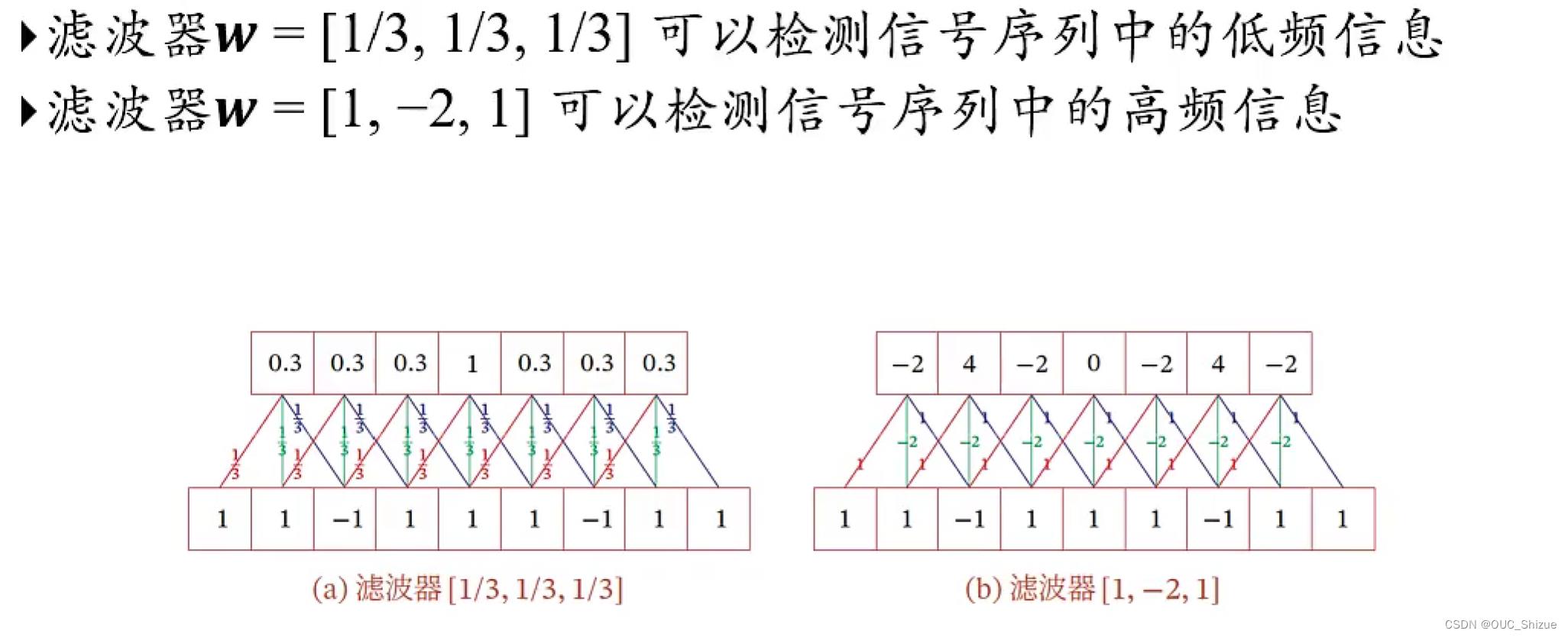
4、卷积扩展

​ 引入滤波器的滑动步长S和零填充P（Padding）

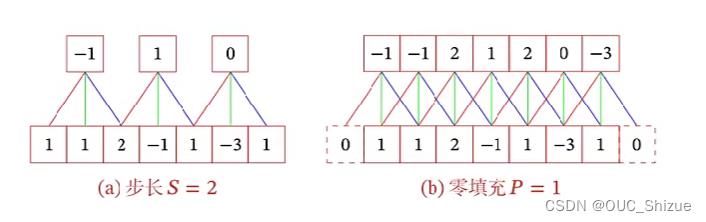
5、卷积类型

（1）按输出长度分类

​ 卷积结果按输出长度不同可以分为三类，在早期文献中，卷积一般默认窄卷积，目前文献中一般默认未等宽卷积

• 窄卷积，步长S=1，两端不补零P=0，输出长度为M-K+1
• 宽卷积，S=1，P=K-1，输出长度为M+K-1
• 等宽卷积，S=1，P=(k-1)/2，输出长度M

（2）按维数分类

​ 由于图像模块常用二维卷积，因此特别介绍

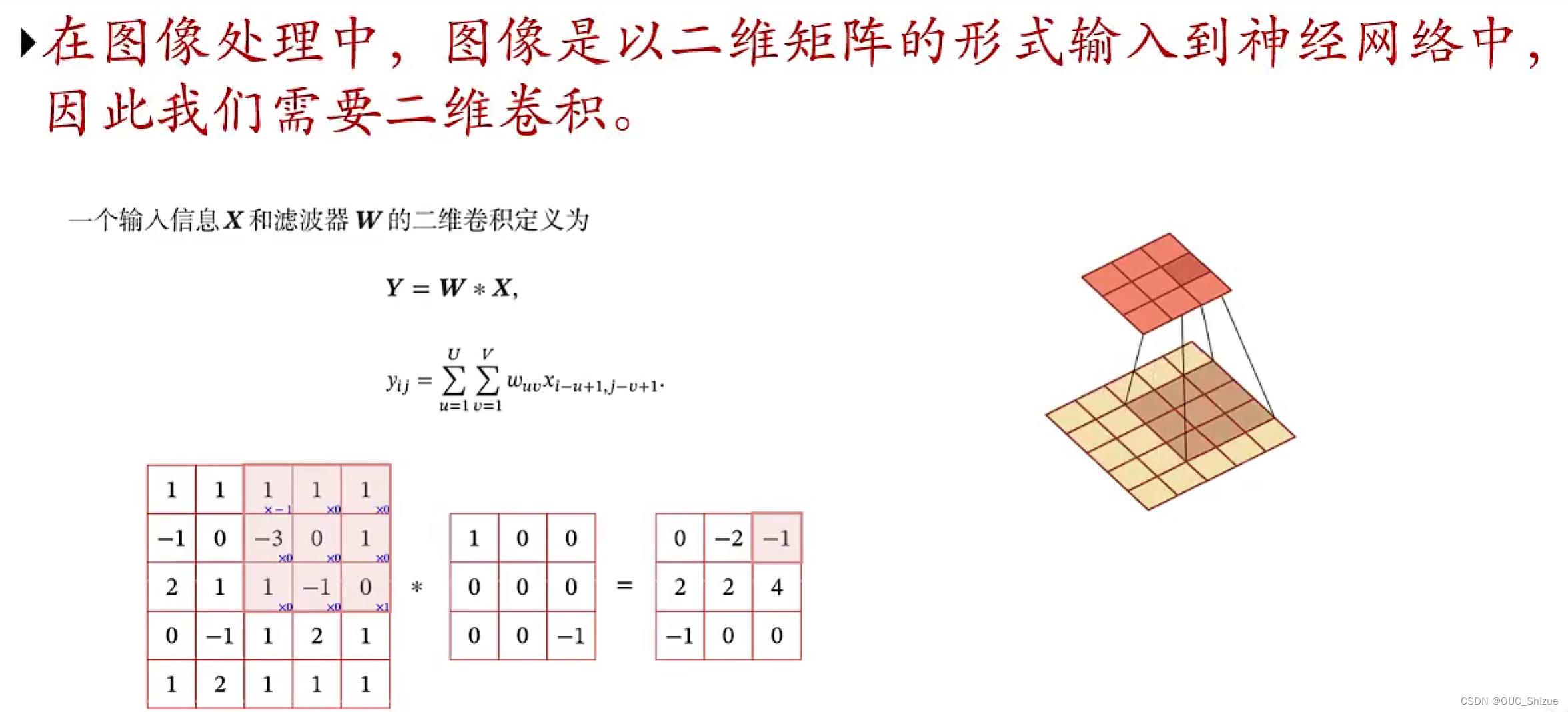
6、卷积作为特征抽取器

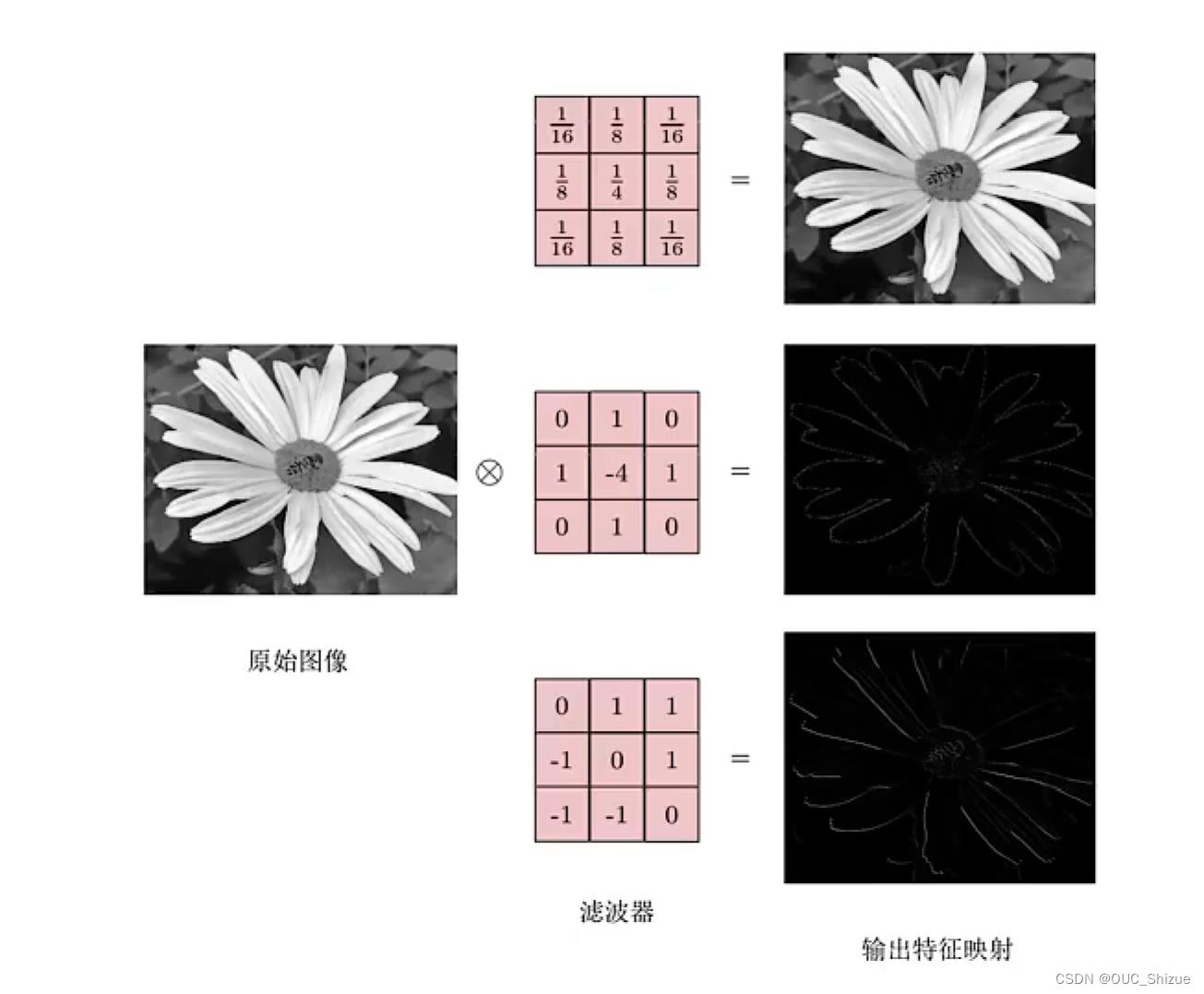
三、卷积神经网络

1、用卷积层代替全连接层

2、互相关

• 计算卷积需要进行卷积核翻转（但由于w是可学习的参数，因此翻转是非必要的）
• 卷积操作的目的：提取特征

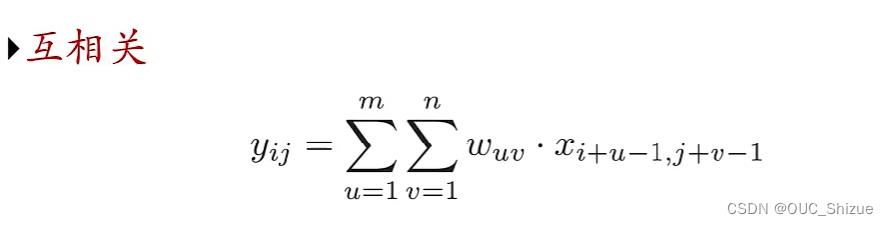
3、多卷积核

（1）多卷积核目的

​ 将卷积核看做是特征提取器，引入多卷积核可以增强卷积层的能力

（2）以两维为例

​ 特征映射（Feature Map）：图像经过卷积后得到的特征

​ 卷积层：输入：D个特征映射M×N×D

​ 输出：P个特征映射M’×N’×P

4、卷积层的映射关系

5、卷积层

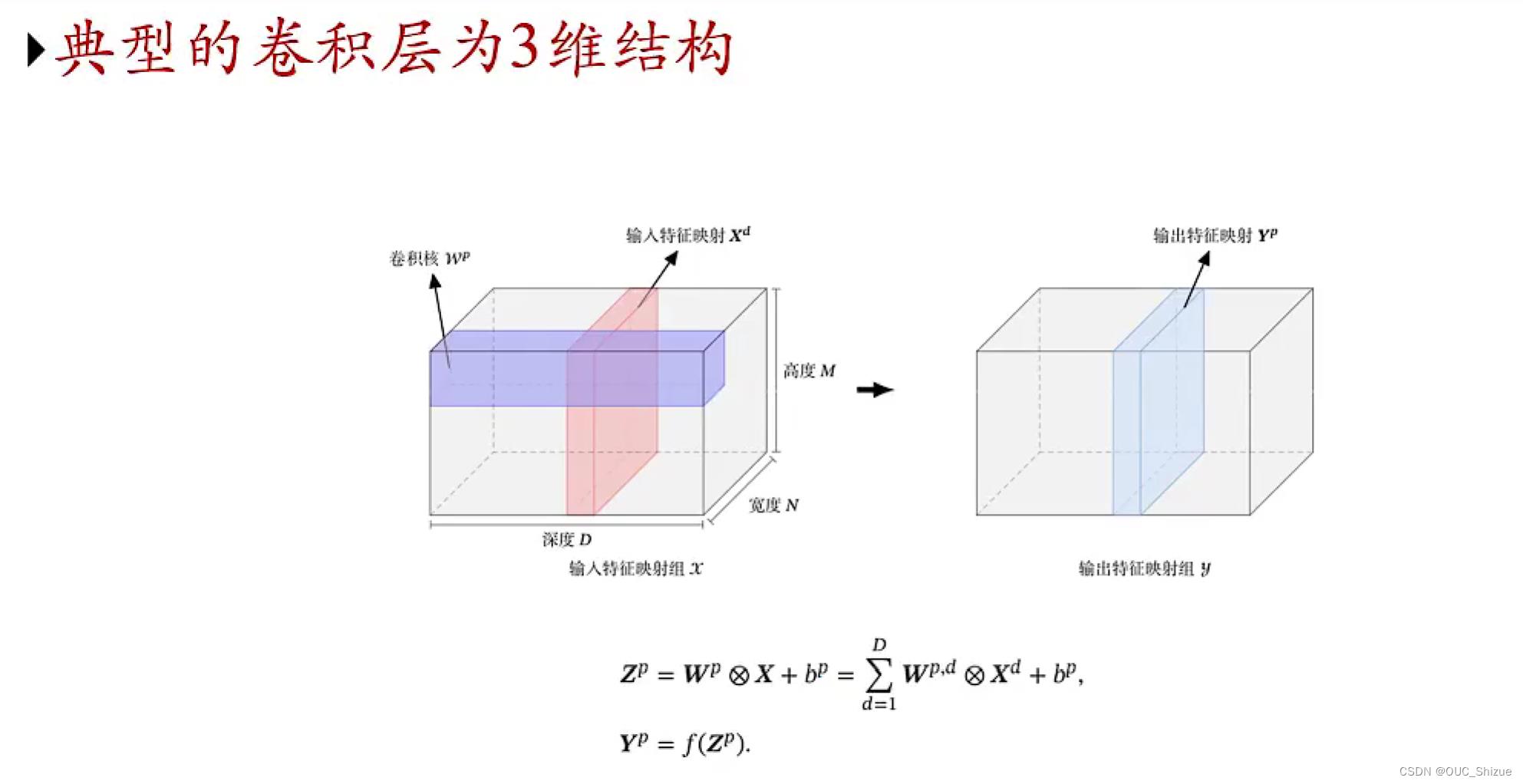
6、汇聚层 Pooling Layers

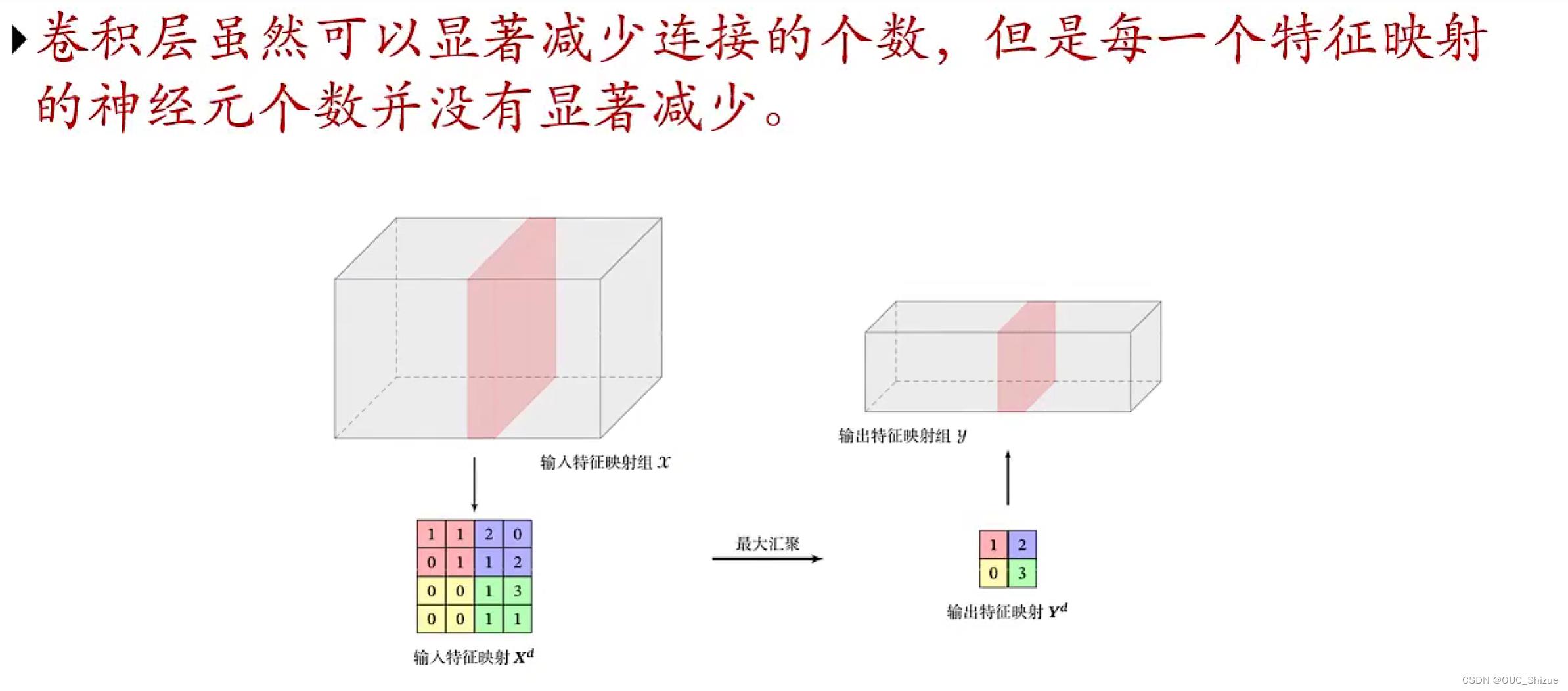
7、卷积网络结构

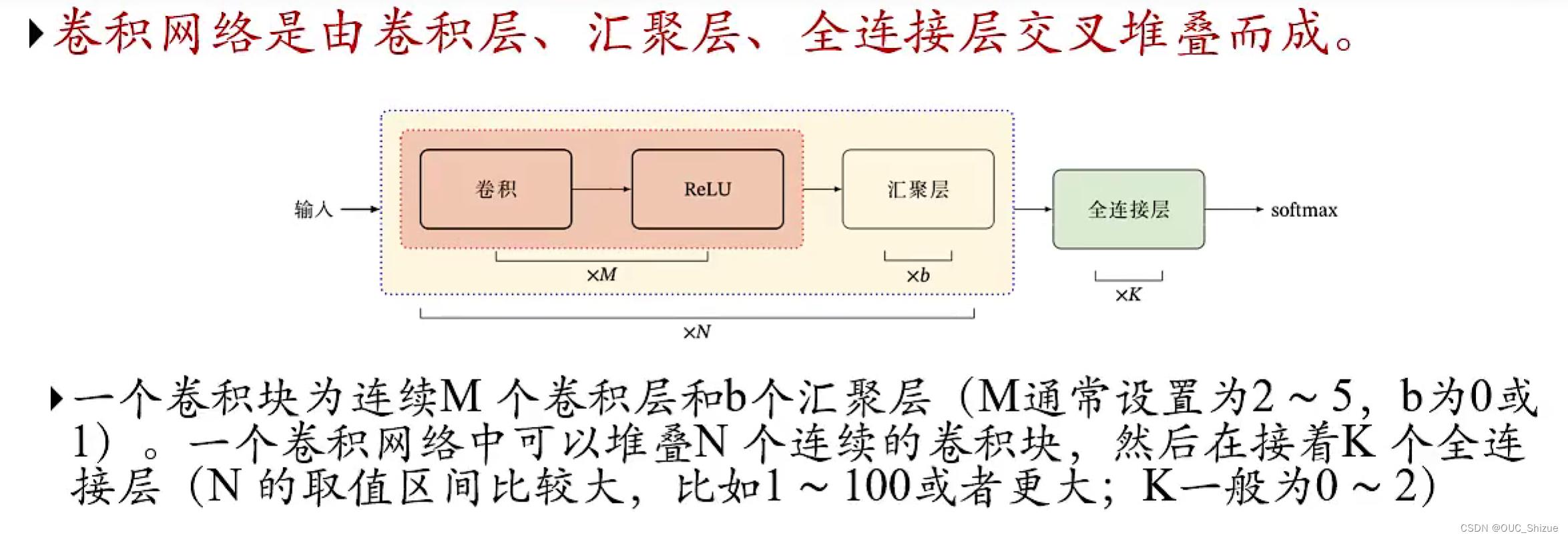
典型结构：

• 趋向于小卷积、大深度
• 趋向于全卷积

四、其他卷积类型

1、空洞卷积

（1）如何增加输出单元的感受野

• 增加卷积核的大小
• 增加层数
• 在卷积之前进行汇聚操作

（2）空洞卷积

​ 通过给卷积核插入“空洞”来变相增加其大小

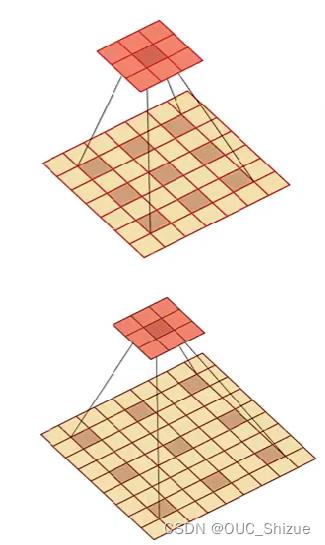
2、转置卷积/微步卷积

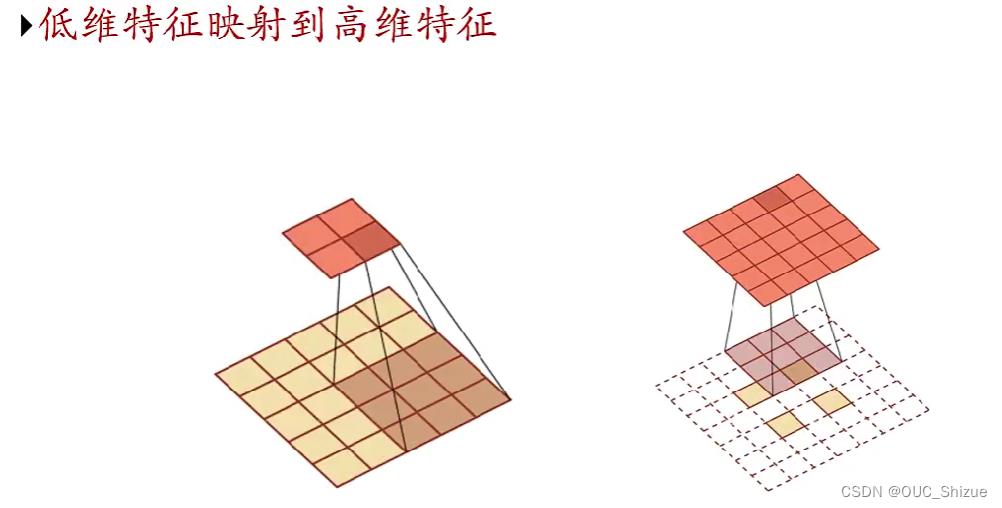
五、典型的卷积神经网络

1、LeNet-5

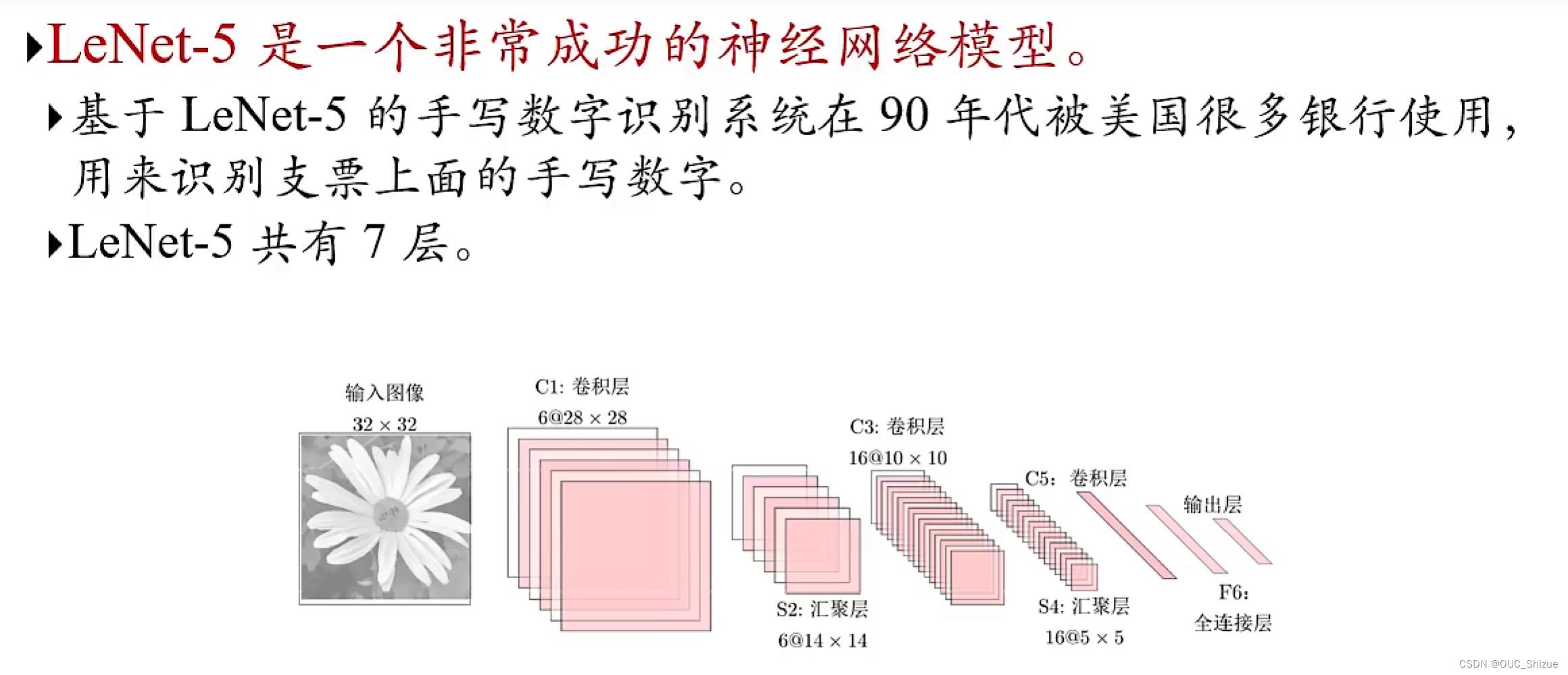
2、Large Scale Visual Recognition Challenge中优秀模型

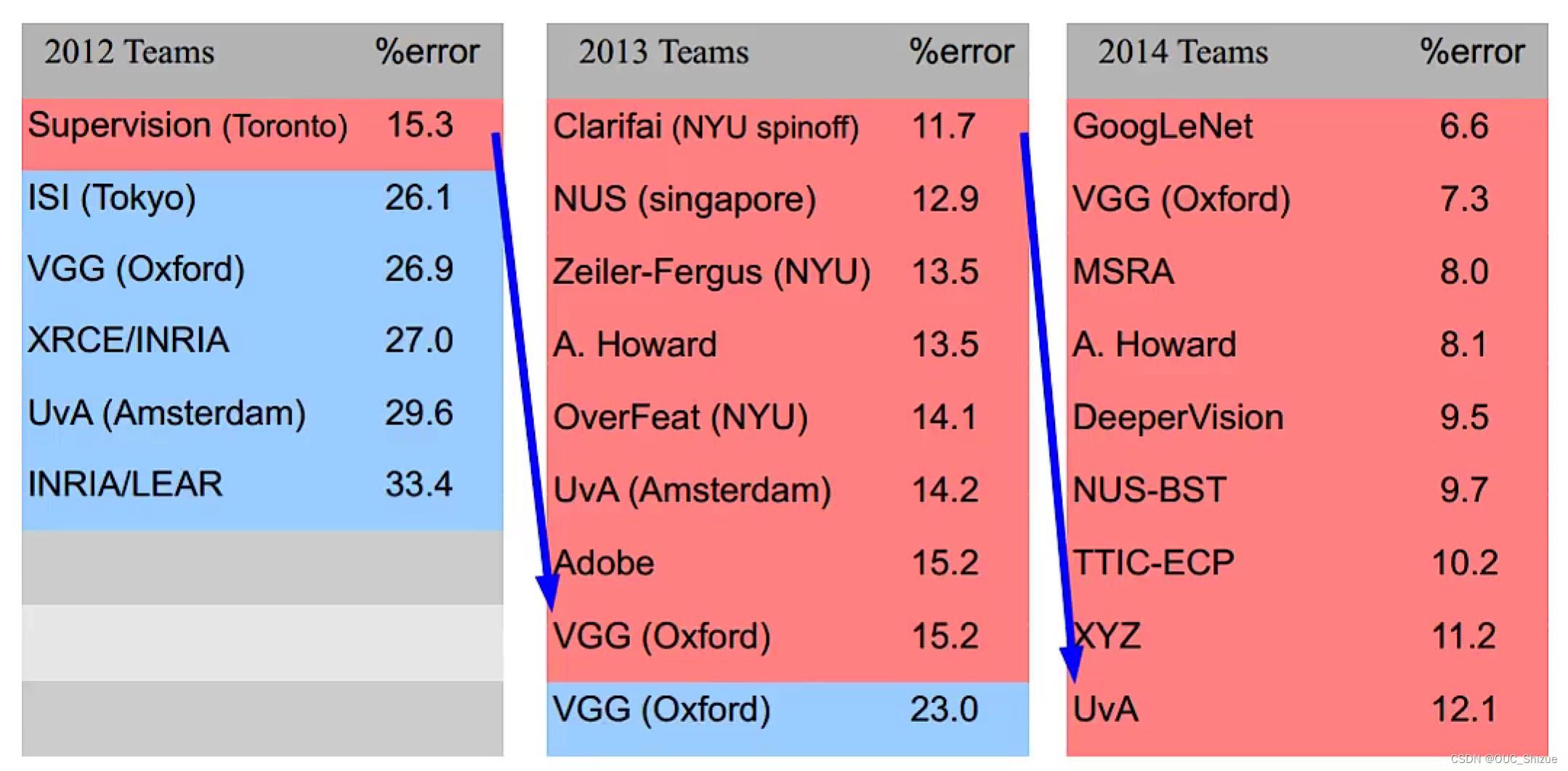
2015为ResNet

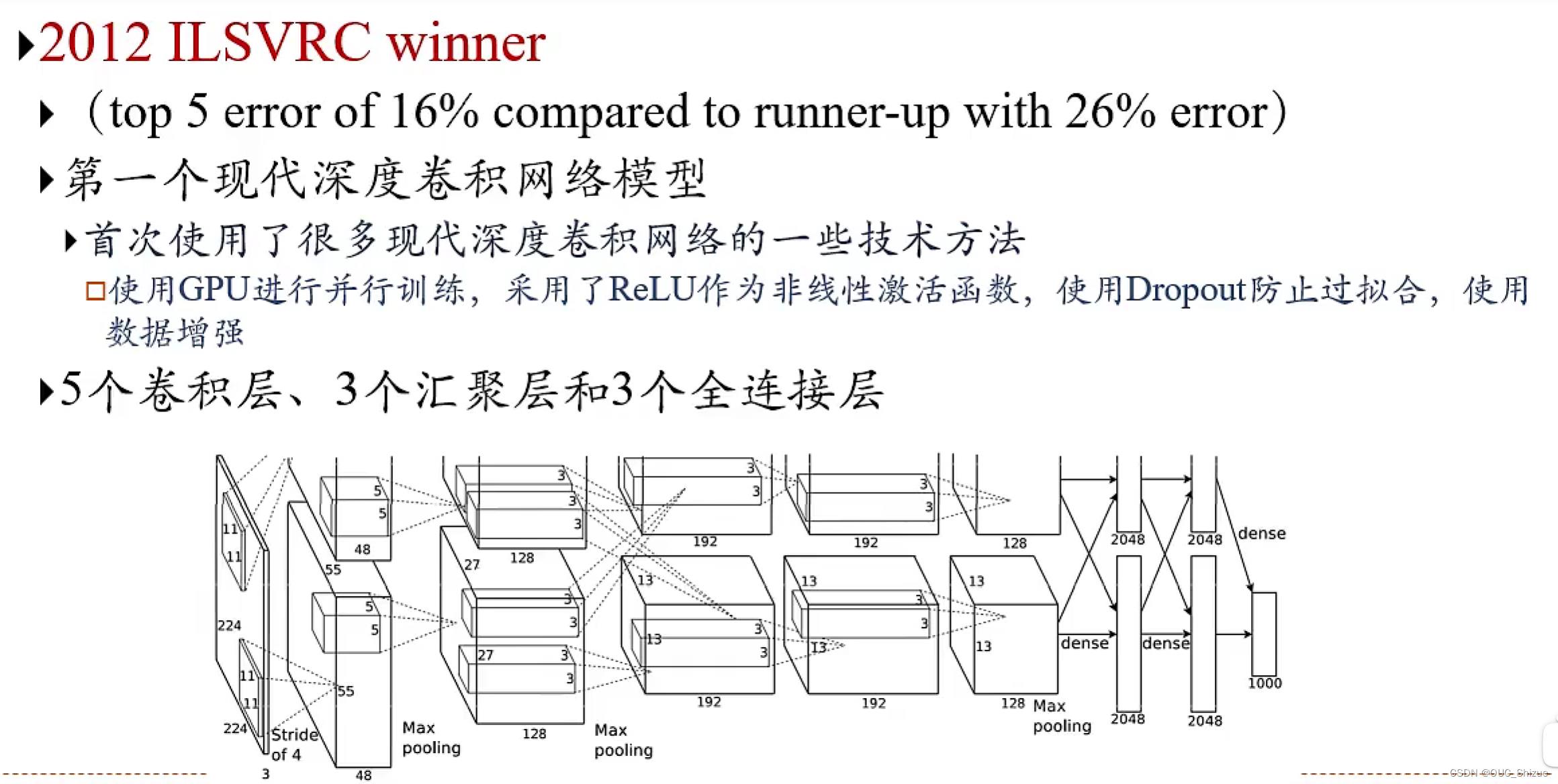
3、AlexNet

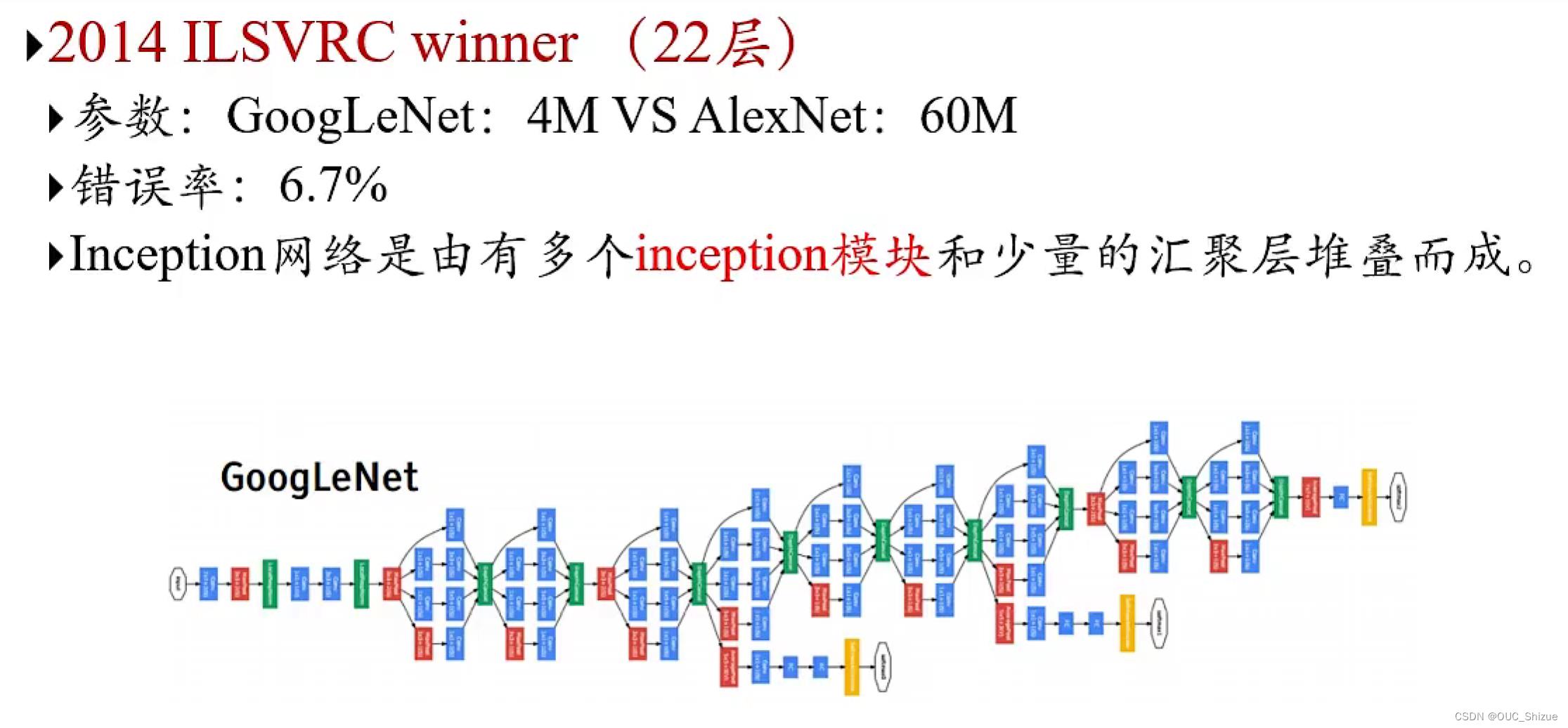
4、Inception网络

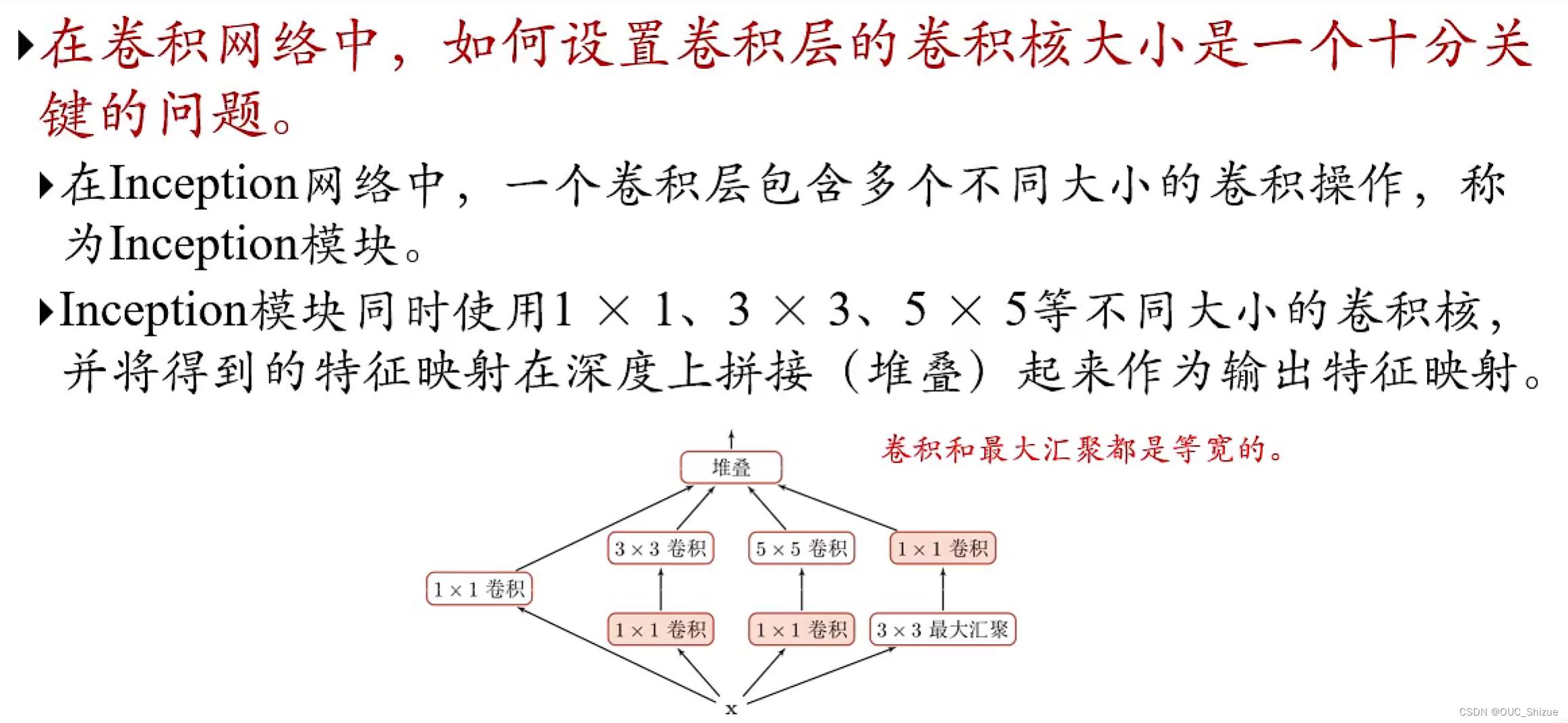
（1）Inception模块v1

​ 穷举各类卷积再堆叠，大大提高得到的特征丰富程度

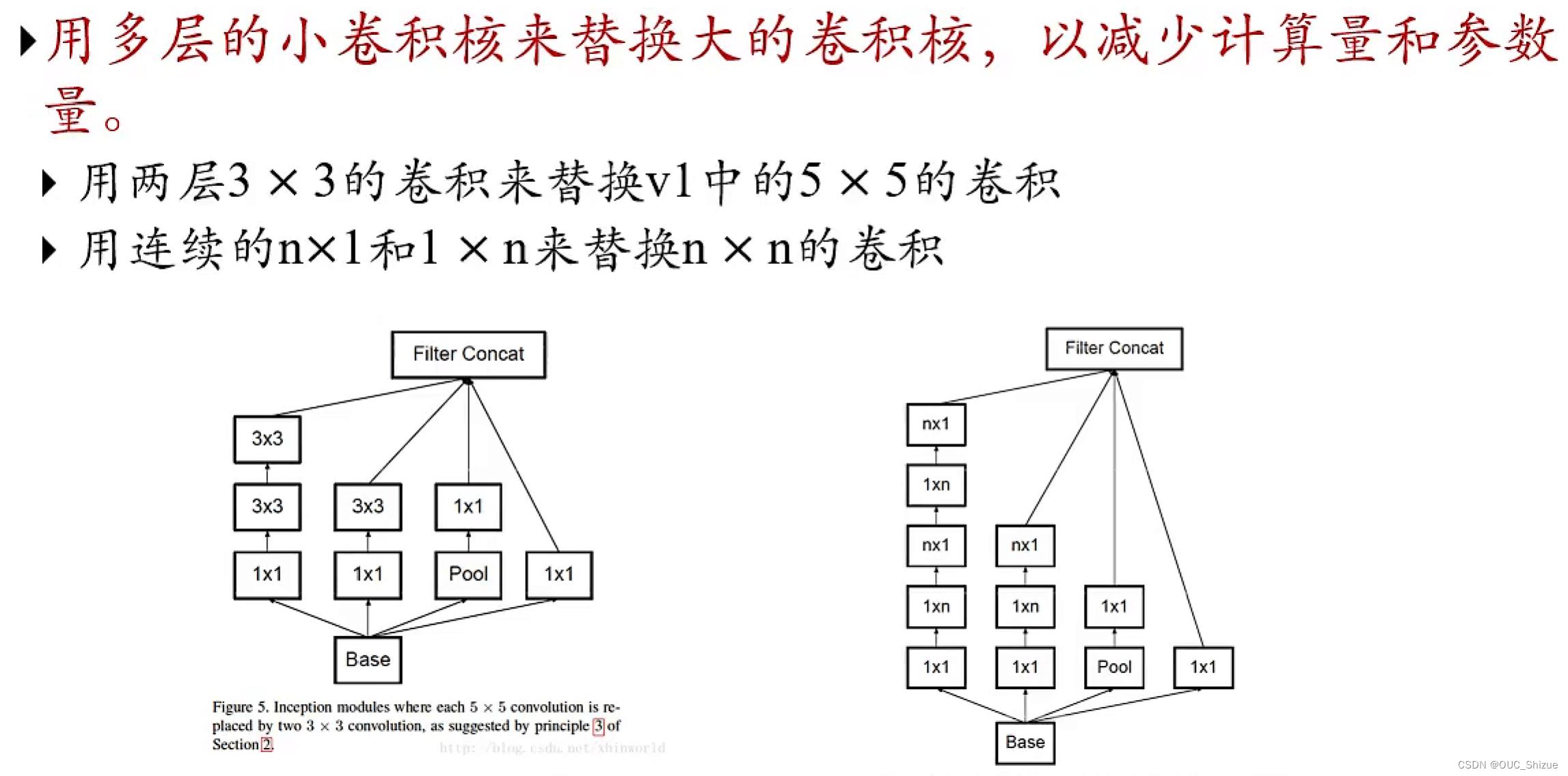
（2）Inception模块v3

5、残差网络 Residual Network，ResNet

（1）概览

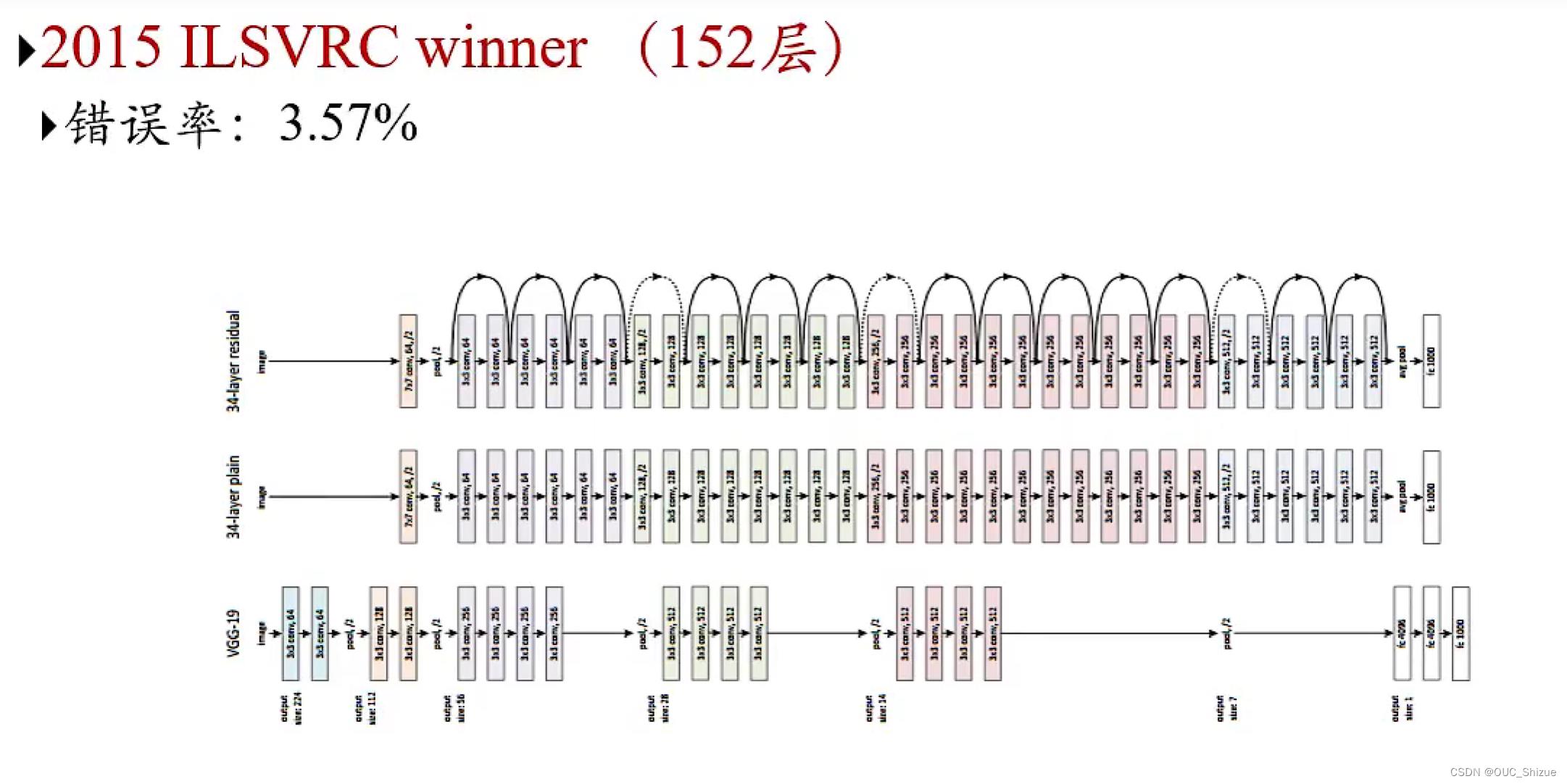
（2）定义

（3）残差单元

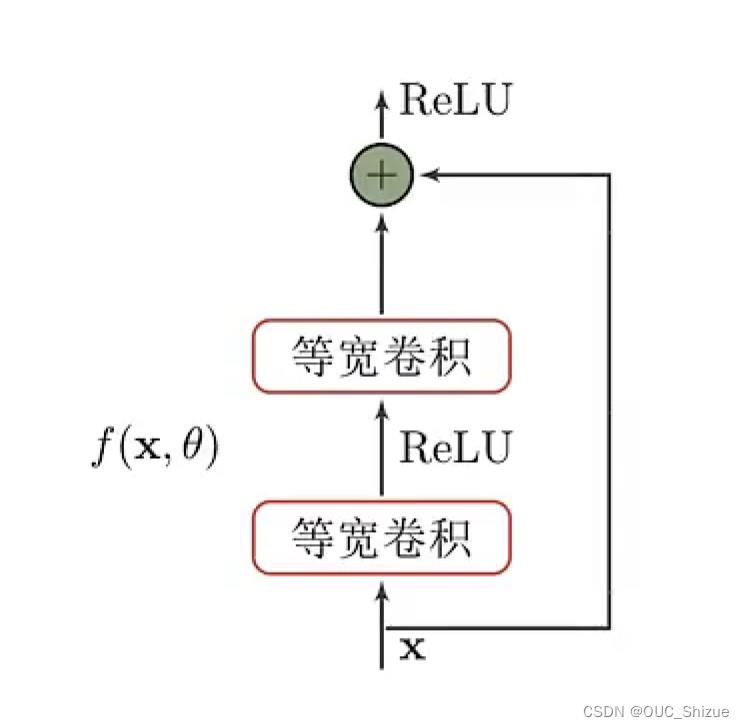
（4）残差应用的意义

​ 残差的连接，或者说直连边是深度堆叠必不可少的技术，其使得梯度dh(x)/dx=1+df(x,θ)/dx，由于有1的存在，因此链式法则连乘之后不会出现梯度消失的现象，故可以大量堆叠

六、卷积神经网络的应用

1、AlphaGo

2、目标检测 Object Detection

3、像素级图像分割 RCNN

4、光学识别 OCR

七、卷积应用到文本

1、Ngram特征与卷积

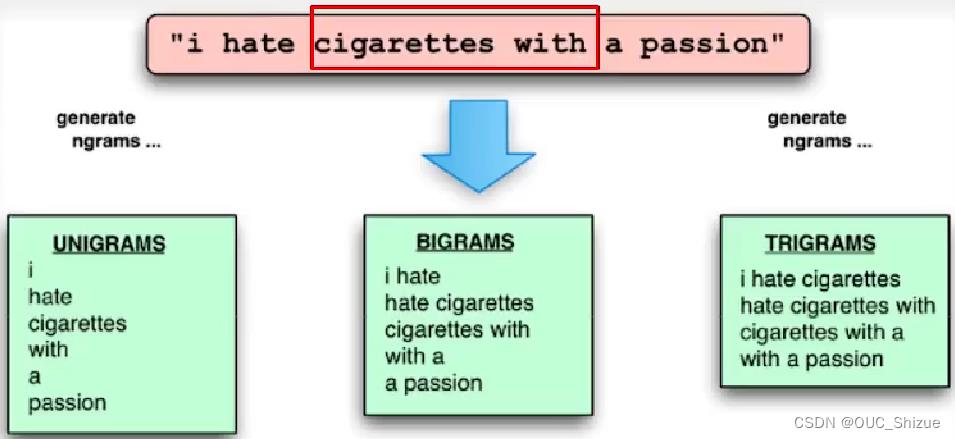
2、基于卷积模型的句子表示

​ 通过查表将单词编程向量

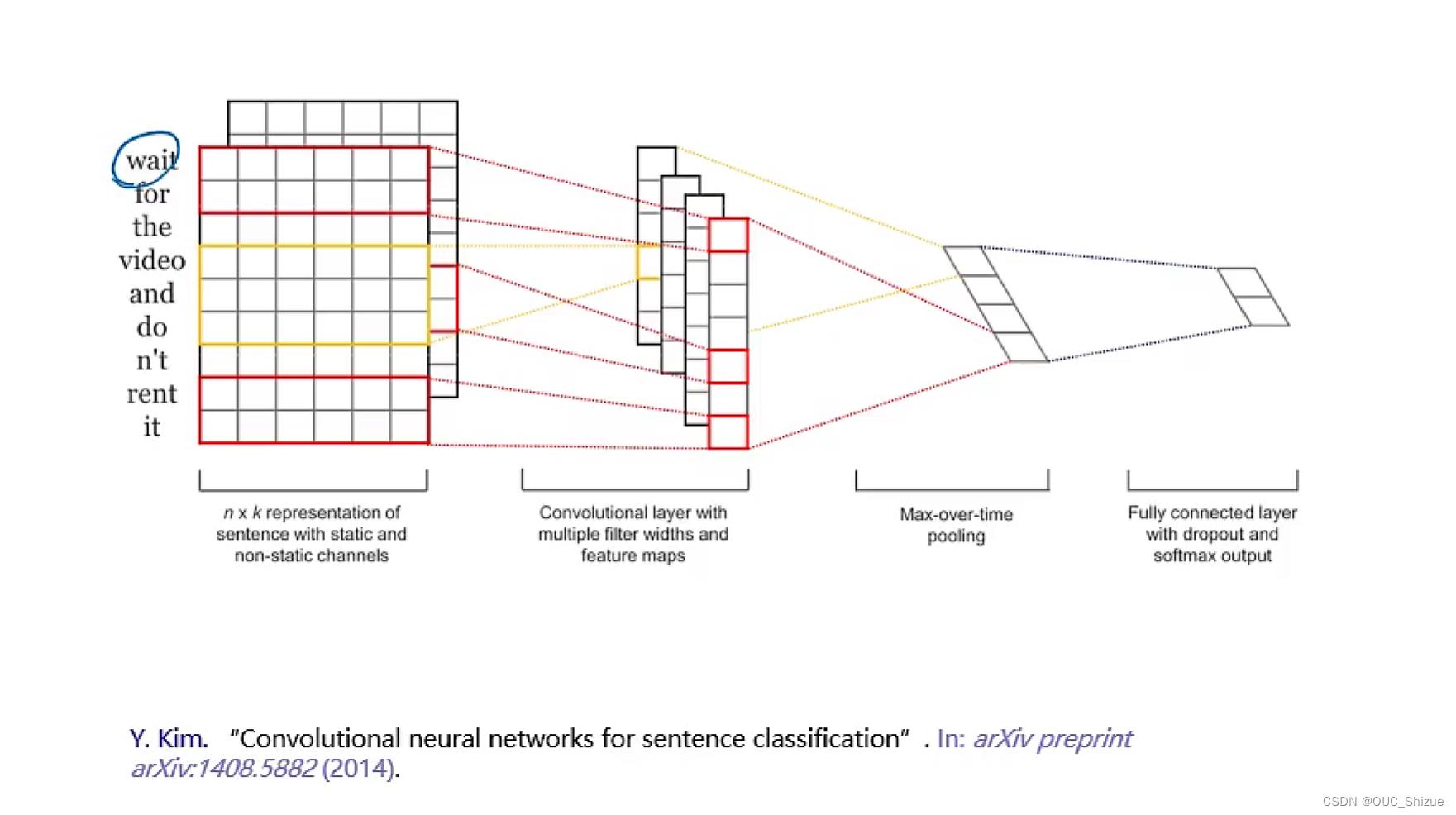
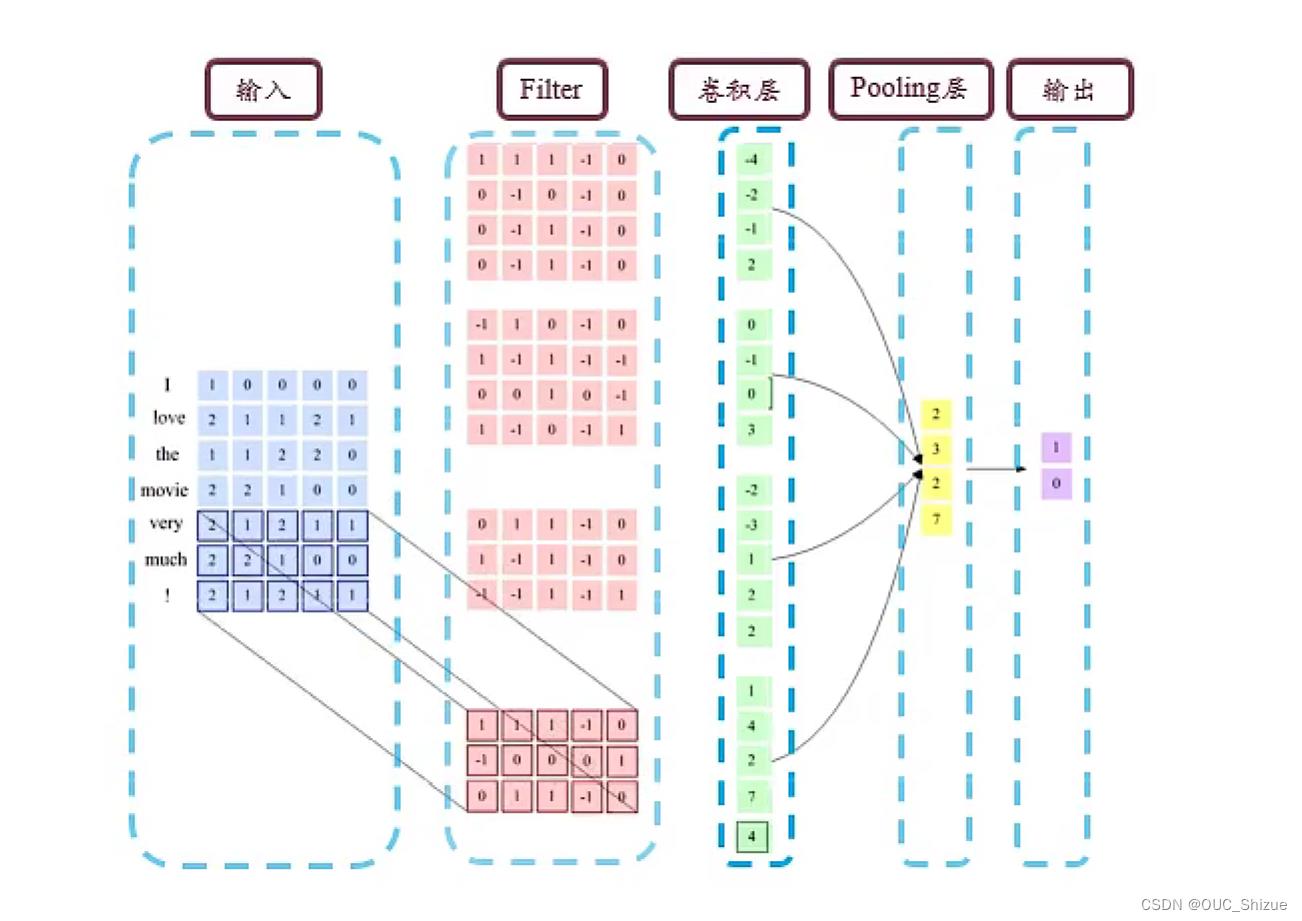
第五章：循环神经网络

一、给前馈神经网络增加记忆力

1、前馈网络特点 FNN

• 相邻两层之间存在单向连接，层内无连接
• 构成一个有向简单图
• 输入和输出的维数是固定的，不能任意改变
• （全连接前馈网络）无法处理变长序列数据

2、有限状态自动机 Finite Automata

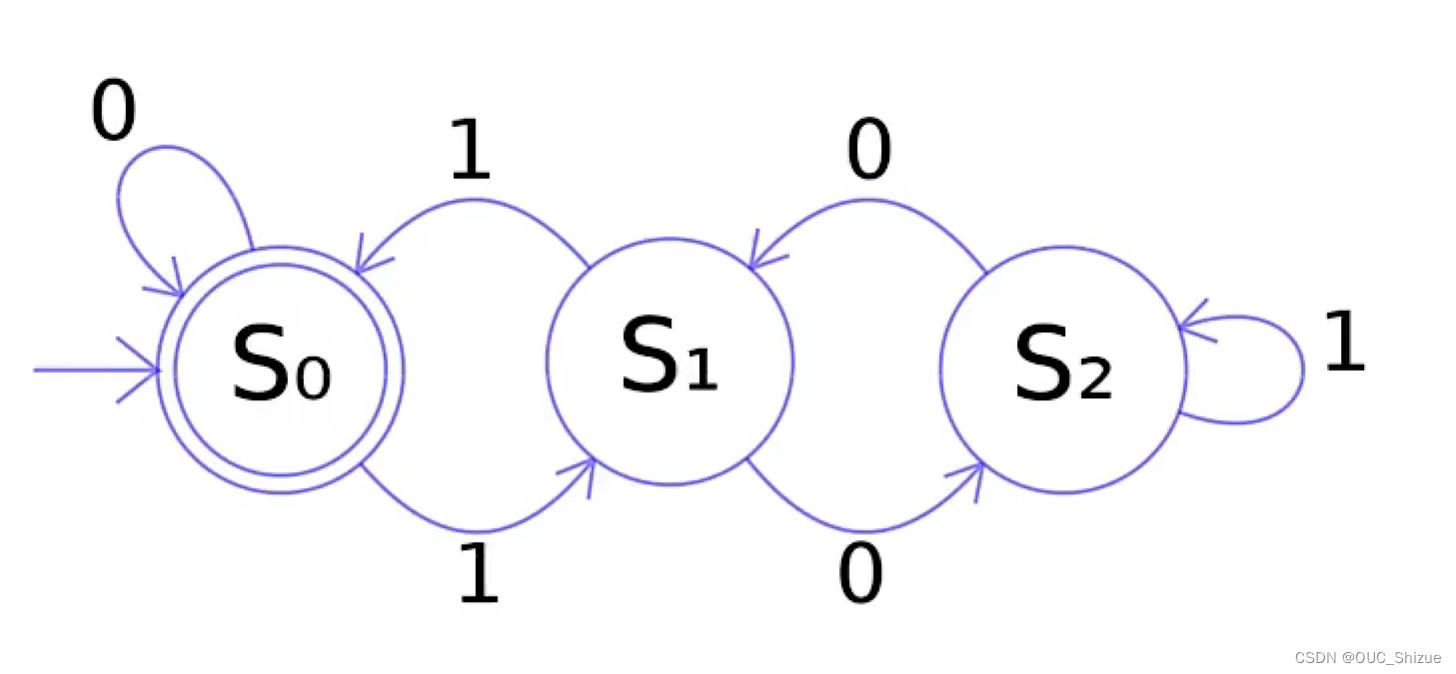
3、图灵机

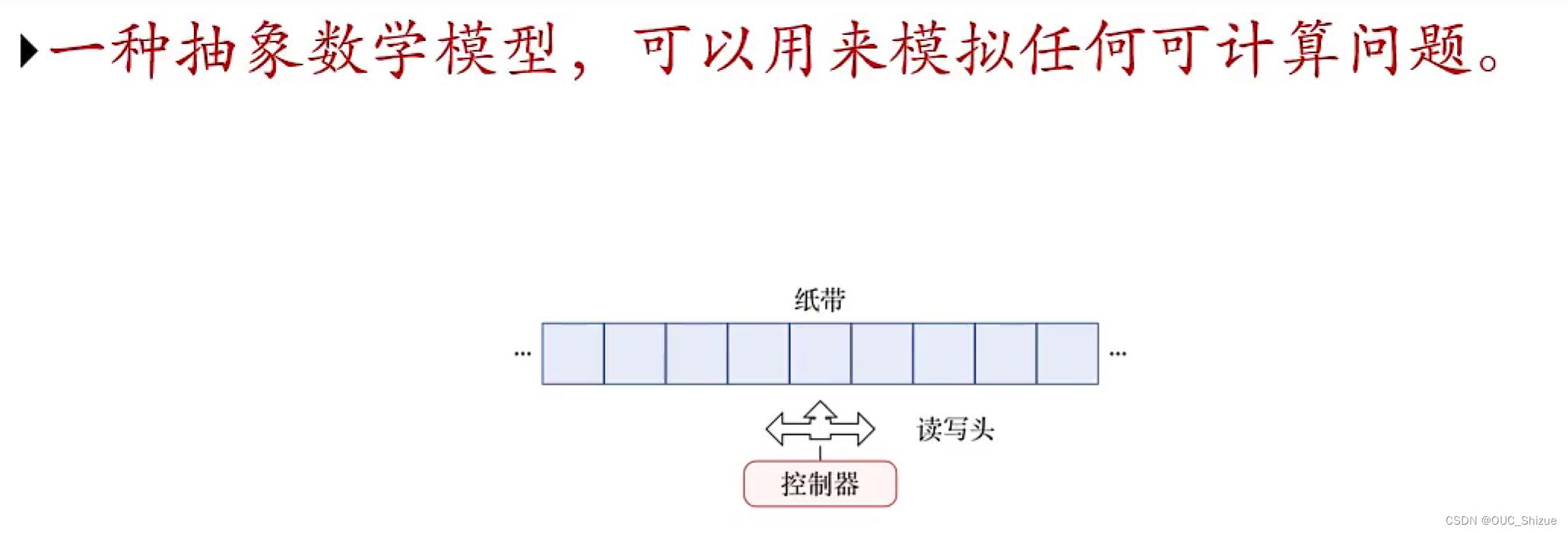
4、时延神经网络 Time Delay Neural Network，TDNN

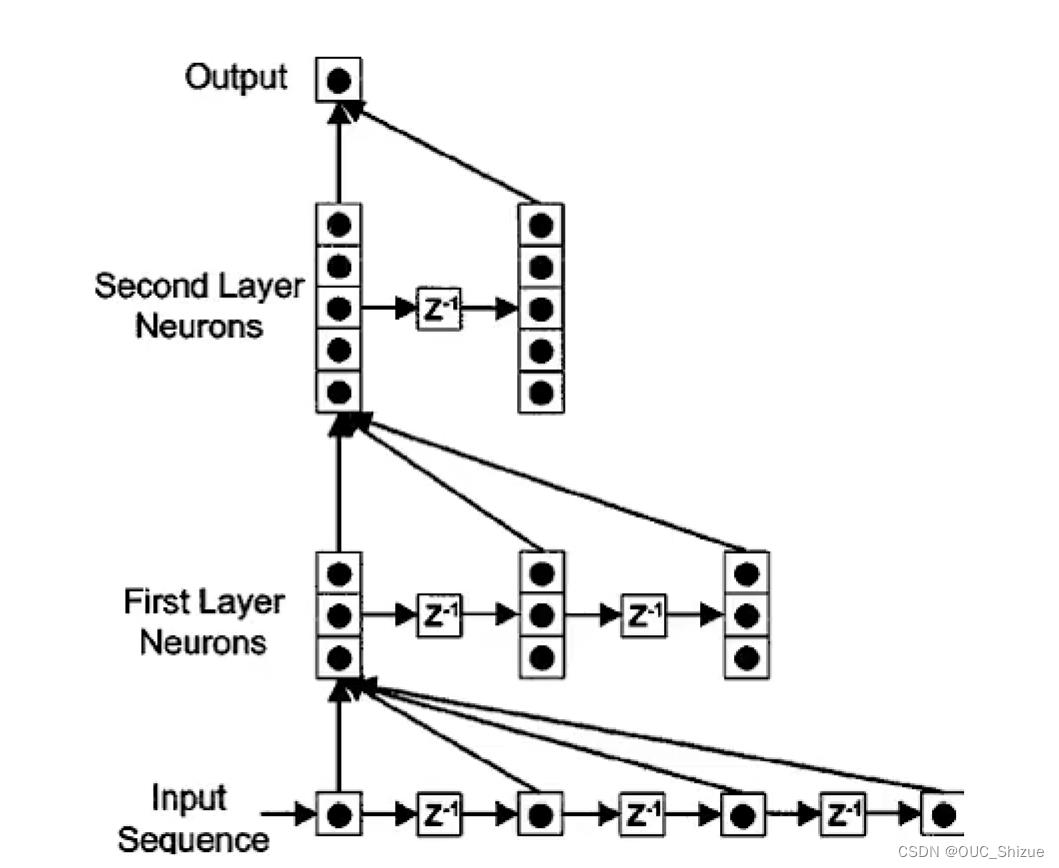
5、自回归模型 Autoregressive Model，AR

6、有外部输入的非线性自回归模型 Nonlinear Autoregressive with Exogenous Inputs，NARX

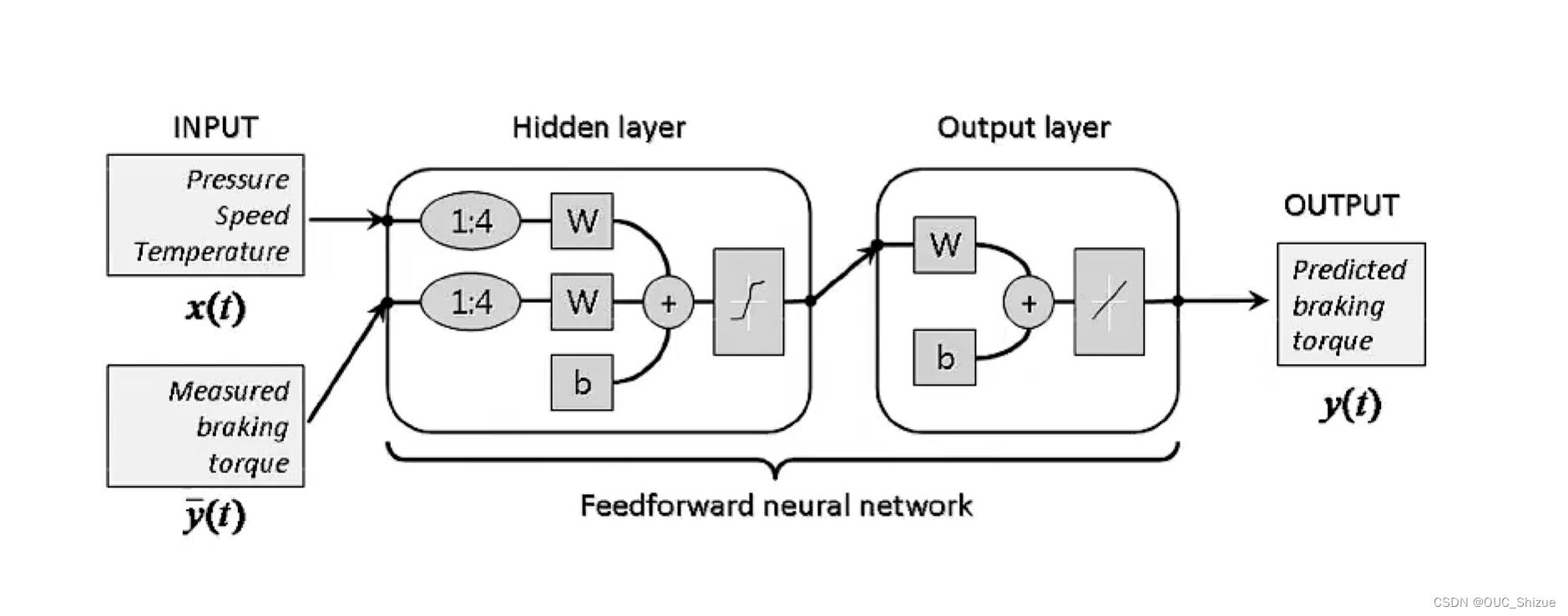
二、循环神经网络 Recurrent Neural Network，RNN

1、图解

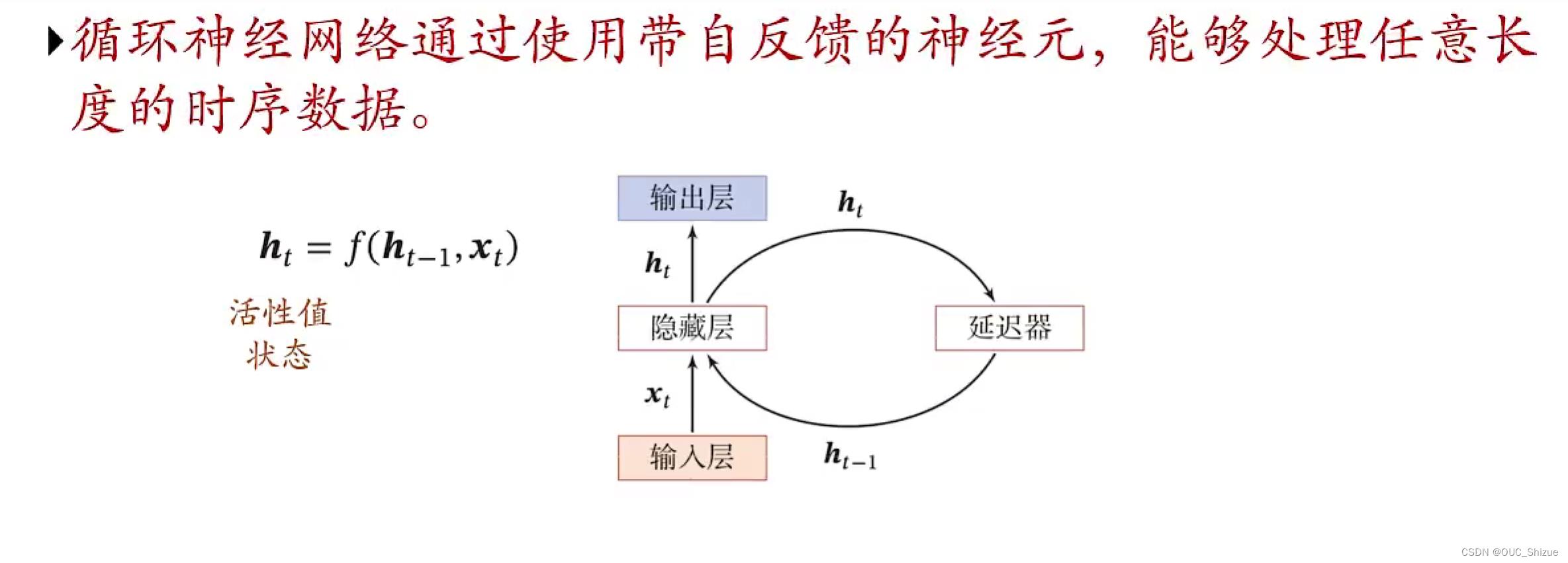
• RNN比FNN更加符合生物神经网络的结构
• RNN已经被广泛应用在语音识别、语言模型以及自然语言生成等任务上

2、按时间展开

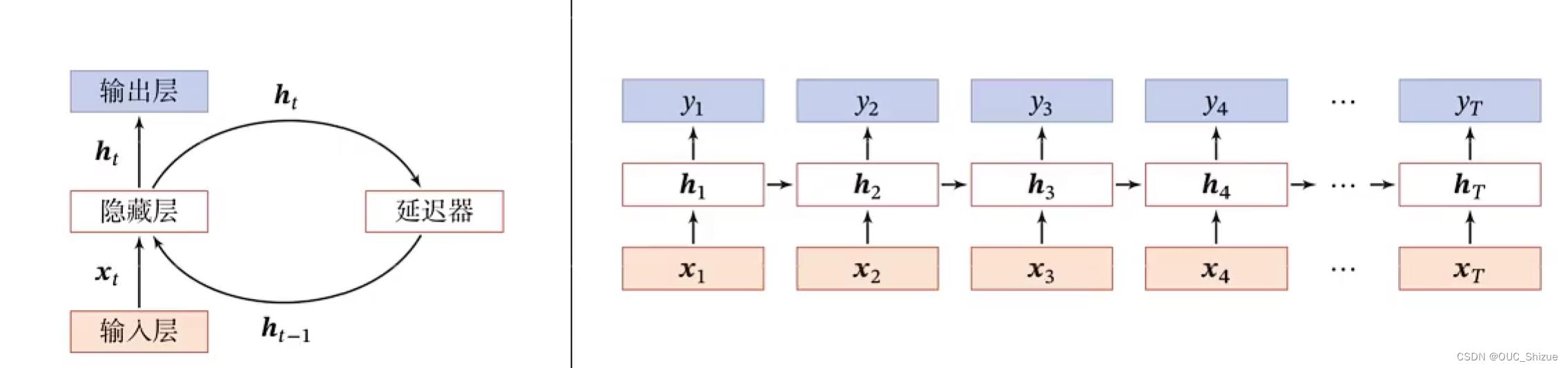
• 时间维度上较浅，需要加深
• 非时间维上较深，需要考虑梯度消失问题

3、简单循环网络 Simple Recurrent Network，SRN

4、图灵完备 Turing Completeness

5、应用

• 输入-输出映射（机器学习模型）
• 存储器（联想记忆模型，例如Hopfield）

三、RNN应用到ML中

1、序列到类别

​ 输入是个序列（向量），输出是个类别

2、情感分类

​ 第一步要将文字查表映射到一个向量作为一个input

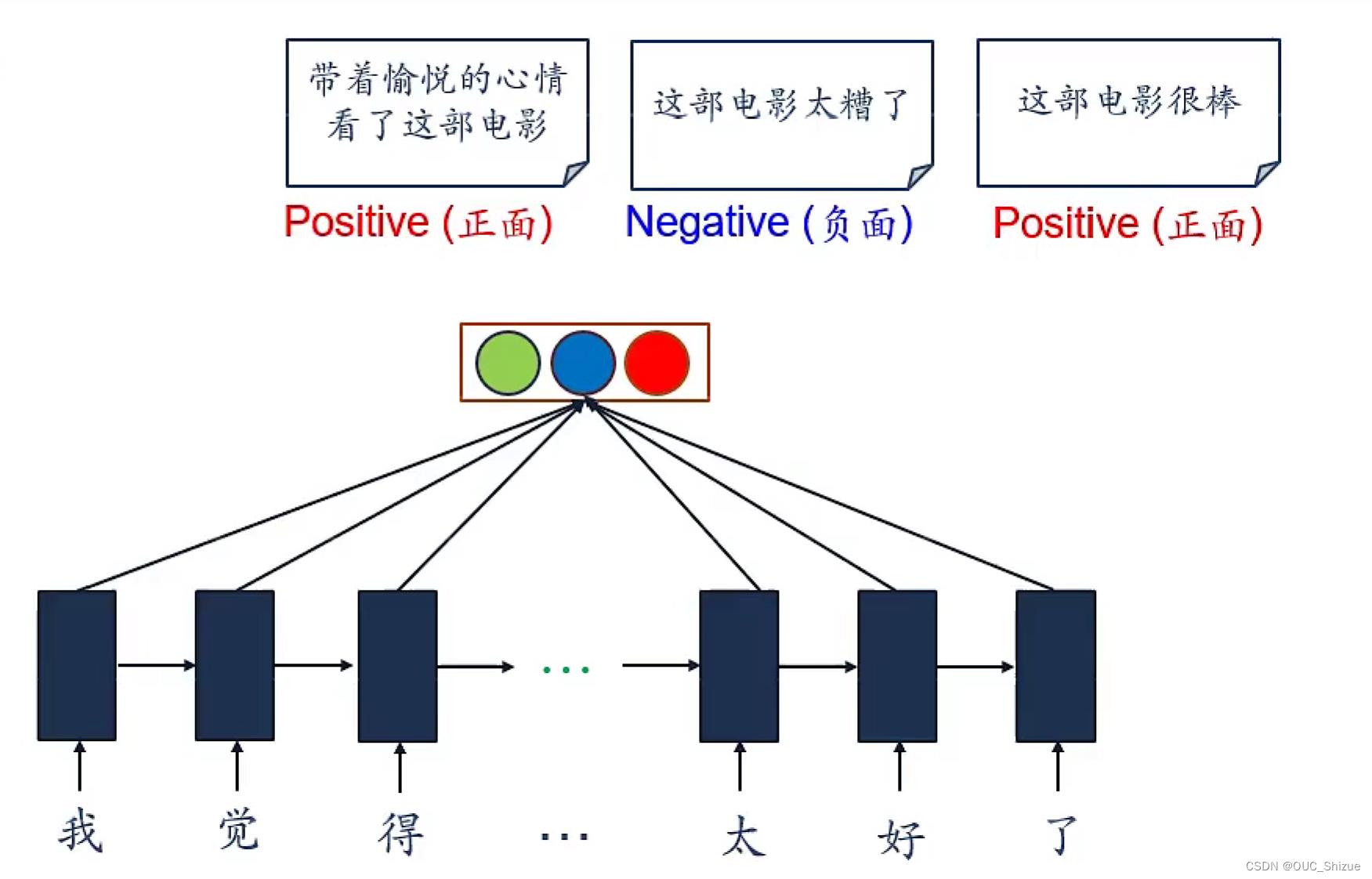
3、同步序列到序列模式

​ 输入是一个序列，输出也是个序列，且是一一对应的

（1）中文分词

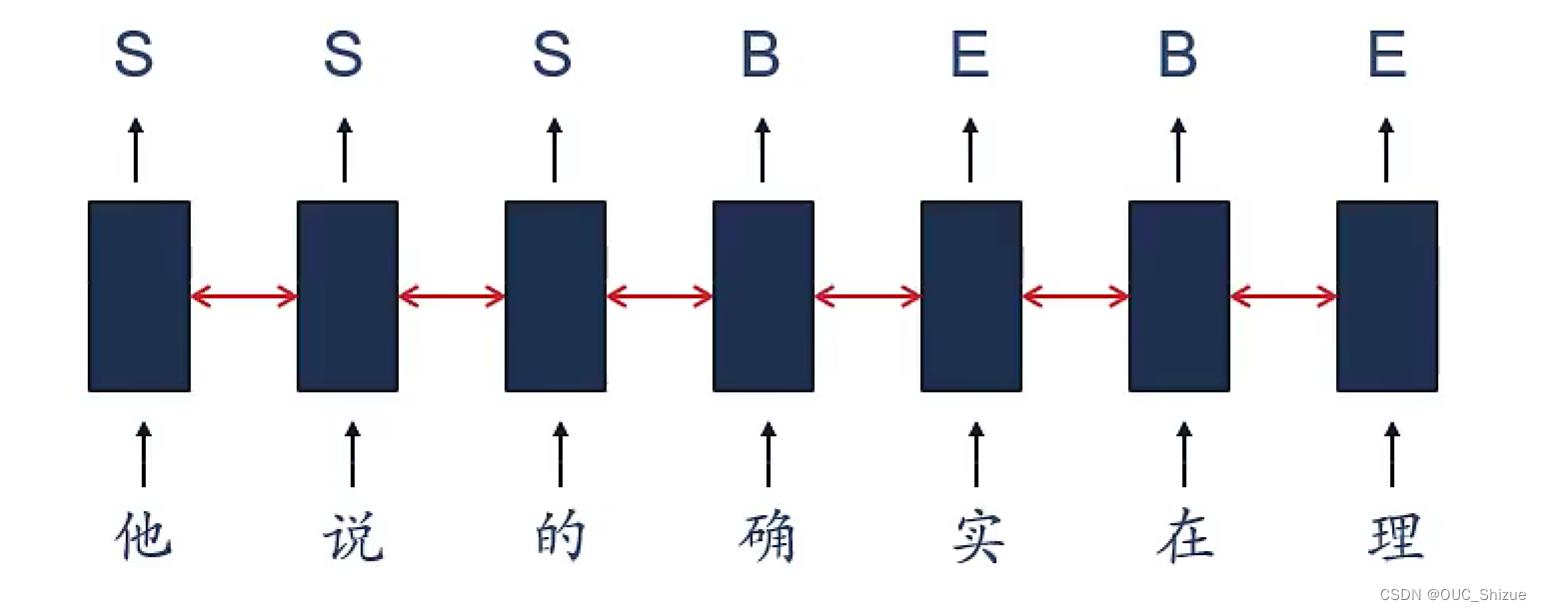
（2）信息抽取 Information Extraction，IE

（3）语音识别

​ Connectionist Temporal Classification，CTC

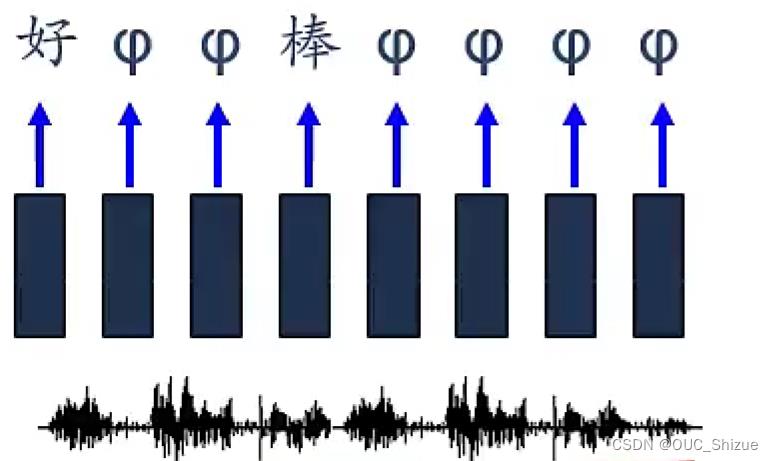
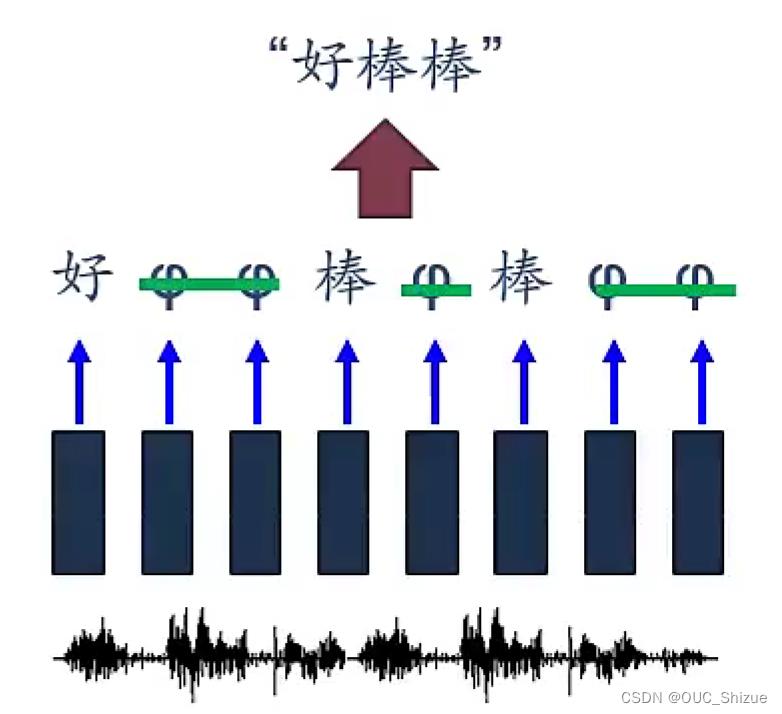
4、异步序列到序列模式

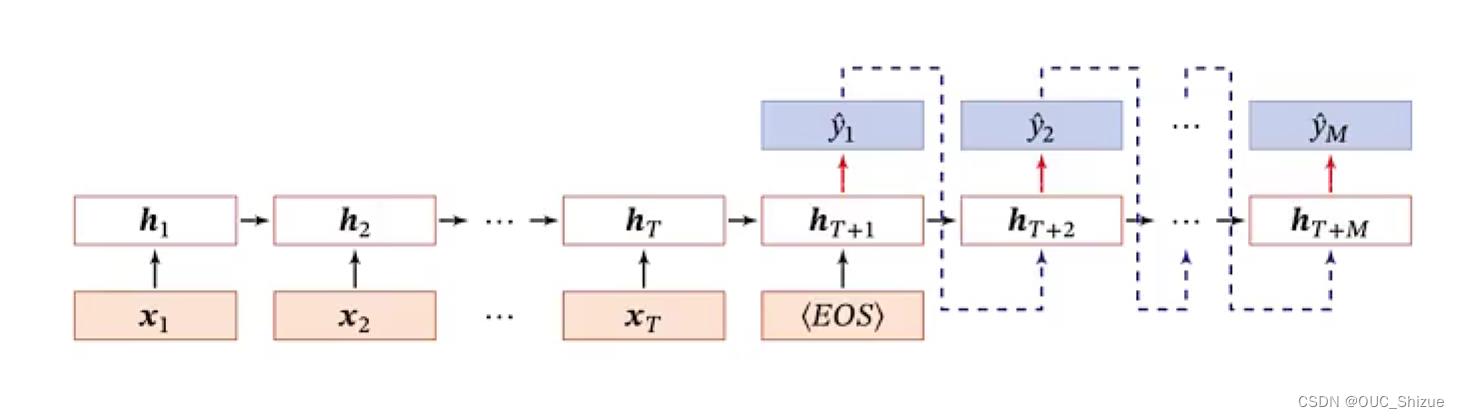
​ 典型应用为机器翻译

四、参数学习

1、损失函数

2、随时间反向传播算法 BackPropagation Through Time，BPTT

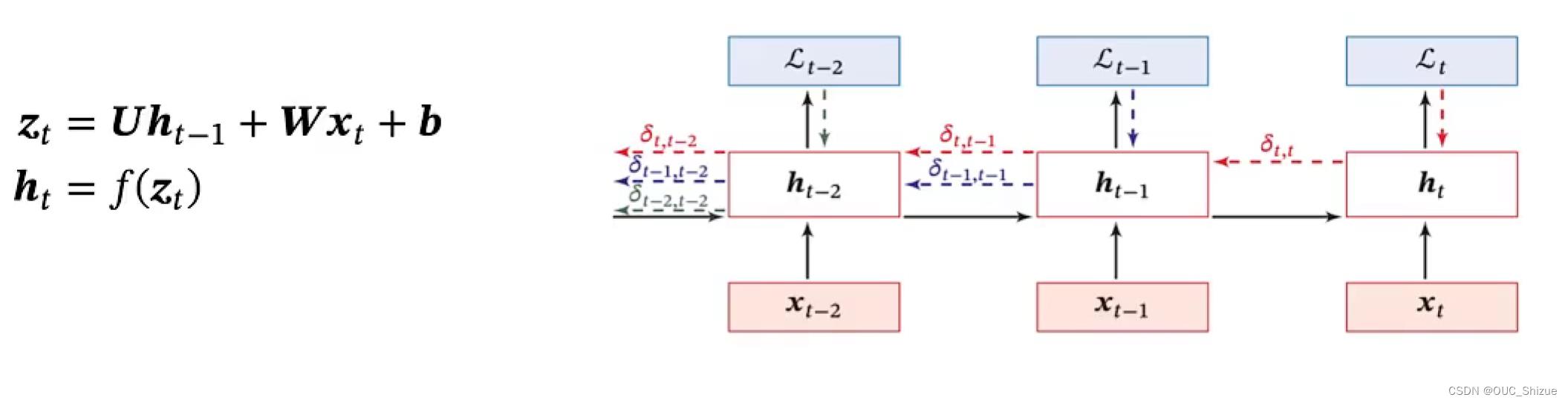
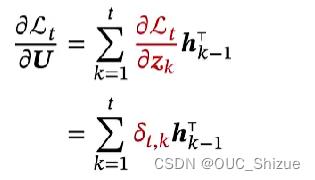
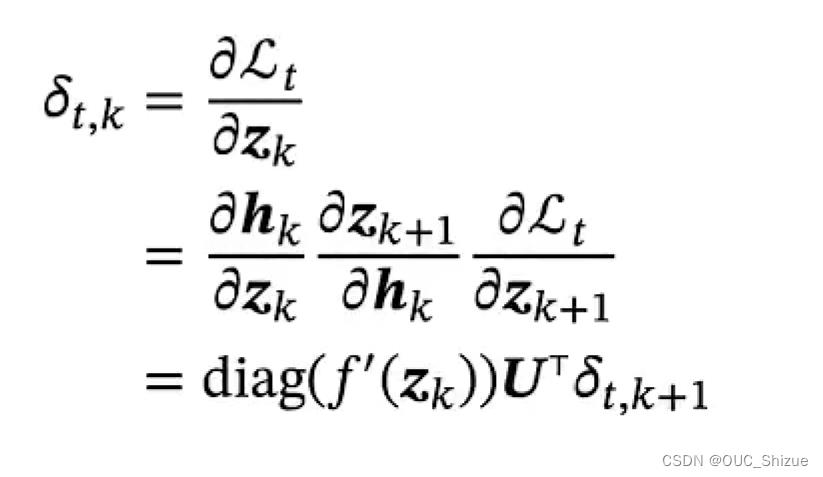
3、梯度

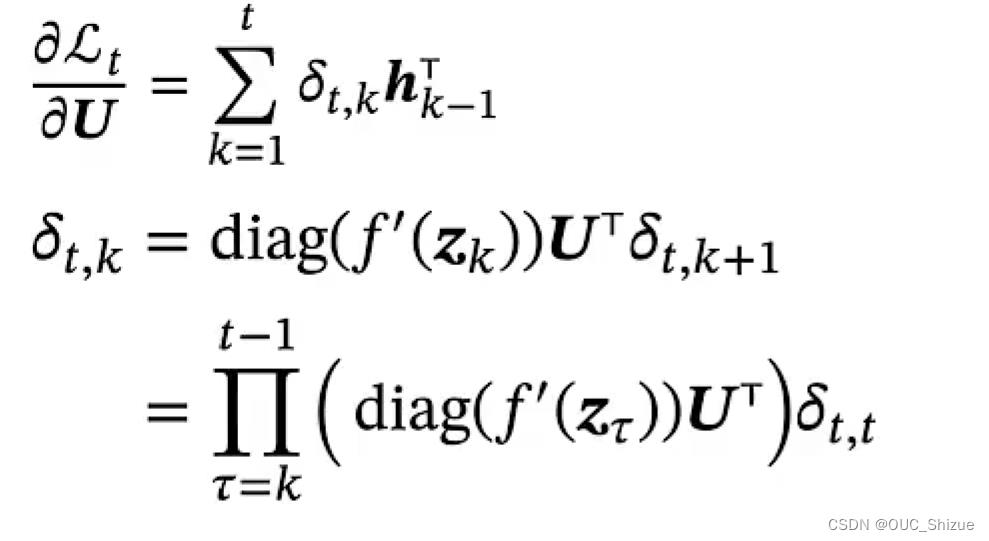
​ 令括号中的部分等于γ，则

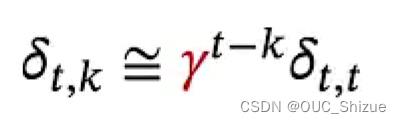
​ 从式子分析，当t-k较大，即两个时间点相隔较远时，若γ>1则梯度->∞，发生梯度爆炸；若γ<1则梯度->0，发生梯度消失

4、长程依赖问题 Long-Term Dependencies Problem

​ 由于梯度爆炸或梯度消失问题，实际上只能学习到短周期的依赖关系；要解决该问题的方法即使得γ=1

五、解决长程依赖问题

1、问题来源

​ 神经网络在时间维度上非常深，容易发生梯度消失或梯度爆炸问题

​ 梯度爆炸可用权重衰减或梯度阶段方法解决；梯度消失则需要改进模型

2、改进方法

​ 循环边改为线性依赖边，但此时ht与ht-1为线性关系，削弱了模型能力

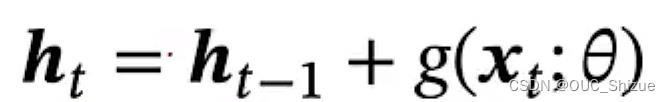
​ 进一步改进，增加非线性

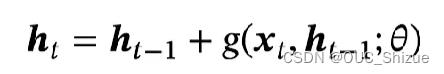
​ 但由于此式子ht一直在增大，当信息饱和时难以更新信息

六、GRU与LSTM

1、门控机制

​ 控制信息的积累速度，包括有选择地加入新的信息，并有选择地遗忘之前累积的信息。

2、门控循环单元 Gated Recurrent Unit，GRU

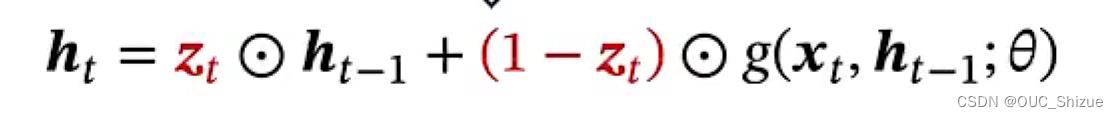
（1）更新门

​ Zt为0~1之间的一个一维向量，也称为更新门

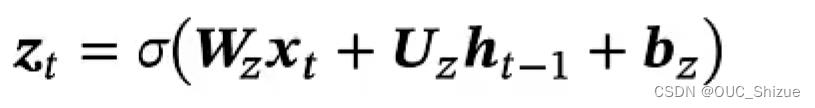
[Mechine Learning] Active Learning

[机器学习] Coursera ML笔记 - 神经网络（Learning） - 标准梯度下降

[机器学习] Coursera ML笔记 - 神经网络（Learning） - 标准梯度下降

Neural Networks: Learning 学习笔记

机器学习- 吴恩达Andrew Ng Week5 神经网络学习Neural Networks Learning知识总结

[机器学习] Coursera ML笔记 - 监督学习（Supervised Learning） - Representation