对称矩阵的压缩存储

Posted 2022-12-14 Luella_G

对称矩阵就是一个方阵。假设有一个N*N的方阵A，若该方阵为对称矩阵，则对于该方阵中的每一个元素Aij，必须满足Aij == Aji（其中 0 <= i <= N-1 , 0 <= j <= N-1）。以矩阵的对角线为分界线，上半部分为上三角，下半部分为下三角。

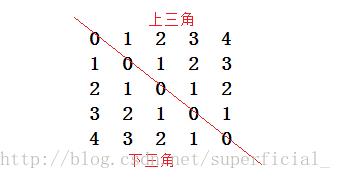
上图即为一个对称矩阵。

若将对称矩阵中的每个元素都保存起来，占用的空间会挺大。根据对称矩阵的性质，我们可以在存储时只存储矩阵的上三角或下三角，最多存储N*(N+1)/2个数据，在数据较多的情况下，会节省很多的空间。

本文将采用下三角存储，将下三角中的数字存储在一个一维数组中，对应的位置为i*(i+1)/2+j（i,j为该数字在对称矩阵中的行列坐标）

 即 i >=j ,SymmetricMatrix[i][j] == Array[i*(i+1)/2+j]

在读取该对称矩阵时，需要的一定是一个完整的方阵，并不是存储的上三角或下三角，我们可以通过行列交换获得未被存储的部分。

对于对称矩阵压缩存储的代码如下：

#include<iostream>

using namespace std;

template<typename T>

class SymmetricMatrix

public:
	SymmetricMatrix(T* array, size_t N)       //构造函数
		:_N(N)
	
		_array = new T[N*(N + 1) / 2];
		size_t index = 0;
		for (size_t i = 0; i < N; ++i)
		
			for (size_t j = 0; j < N; ++j)
			
				if (i >= j)
				
					_array[index++] = array[i * N + j];
				
				else
				
					break;
				
			
		
	
	~SymmetricMatrix()     //析构函数
	
		delete[]_array;
		_array = NULL;
		_N = 0;
	

	T& Access(size_t i, size_t j) 
	
		if (i < j)                     //若为上三角数据，交换行列，得到其对称位置的数据
		
			swap(i, j);
		
		return _array[i*(i + 1) / 2 + j];
	

	void Print()          //读取对称矩阵
	
		for (size_t i = 0; i < _N; ++i)
		
			for (size_t j = 0; j < _N; ++j)
			
				cout << Access(i, j) << " ";
			
			cout << endl;
		
		cout << endl;
	

protected:
	T* _array;     //压缩存储的一维数组
	size_t _N;     //N*N矩阵
;

void TestSymmetricMatrix()

	int array[5][5] = 
	
		0,1,2,3,4,
		1,0,1,2,3,
		2,1,0,1,2,
		3,2,1,0,1,
		4,3,2,1,0
	;
	SymmetricMatrix<int> SM((int *)array, 5);
	SM.Print();


int main()

	TestSymmetricMatrix();
	return 0;

运行结果为：