使用 levenberg-marquardt 优化 欧式空间中的三维点变换关系

Posted 2022-12-13 枯萎的海风

1. 前言

最近涉及到一部分将原先matlab的计算机视觉的相关代码转化成C++实现，其中，有一段是关于空间点变换的。简单来讲，已知欧式空间中的一组空间点$W_1$，在经过某个欧式变换$RT$之后，得到另一组空间点$W_2$，现在在已知$W_1，W_2$的前提下，我们需要求解对应的$RT$。

2. 基本思路

其实这个过程是非常简单的，显然，$W_2 = RT * W_1$， 于是，

$$RT=W_2 * pinv(W_1)$$ , 然而，由于实际过程中存在数据噪声，因而求解得到的 $RT$ 可能是不符合实际物理要求的，这就需要涉及到对 $RT$ 的优化了。

3. matlab 代码

3.1 main

首先生成一组对应的空间点，计算得到他们的变换关系rt 的初值， 然后使用LM优化得到符合物理意义的RT

clear all
clc
close all
warning off

%% generate w3d points   w2(4xn) = rtx(4x4) * w1(4xn) 
[w3d1, w3d2, rtx] = generateW3DPoints(0.01);

rtx_c = w3d2 * pinv(w3d1);

x0 = getRESFromRt(rtx_c);
options=optimset('LargeScale','off','Display','iter','TolFun',1e-30,...
            'TolX',1e-35,'Algorithm','levenberg-marquardt','MaxFunEvals',1e+100,'MaxIter',1000); 
fun = @(x)RTx_youhua(x, w3d1, w3d2);
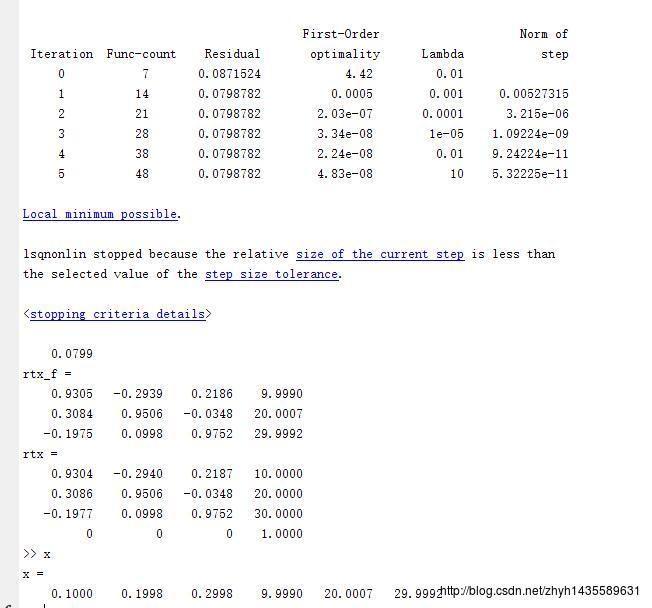
[x, fval] = lsqnonlin(fun, x0, [], [], options);

disp(fval)
rtx_f = getRtFromRES(x)
rtx

w3d1_t = w3d1';
w3d2_t = w3d2';
w3d1_t(:, 4) = 1:size(w3d1_t, 1);
w3d2_t(:, 4) = 1:size(w3d2_t, 1);
save('w3d1.txt', 'w3d1_t', '-ascii', '-double')
save('w3d2.txt', 'w3d2_t', '-ascii', '-double')

3.2 generateW3DPoints

使用meshgrid生成空间点, noise_level 是误差水平的参数

function [w3d1, w3d2, rtx] = generateW3DPoints(noise_level)
   [X, Y, Z] = meshgrid(1:10, 1:10, 1:2);    
    w3d1 = [X(:)'; Y(:)'; Z(:)'; ones(1, length(X(:)))];
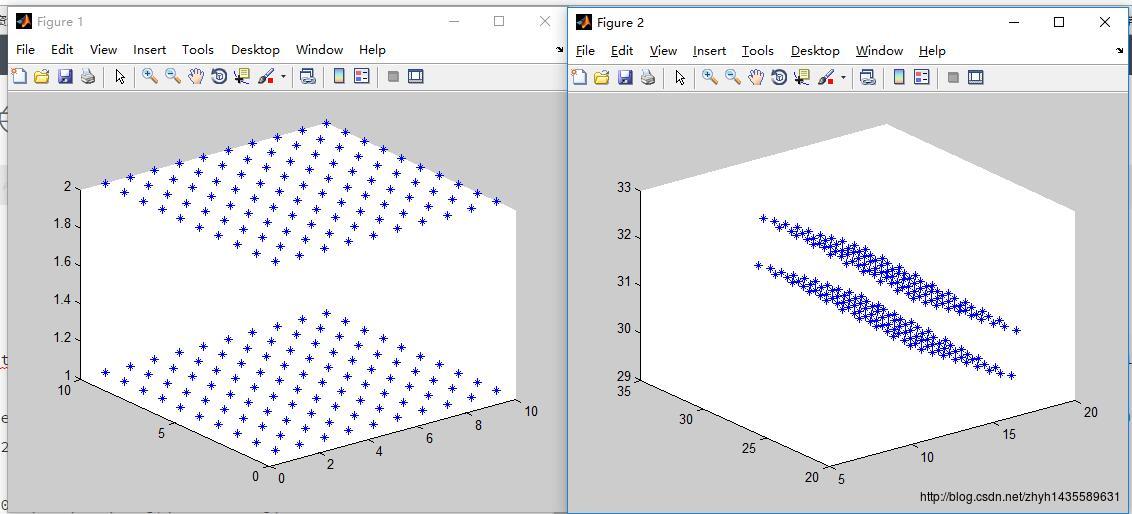
    figure, plot3(w3d1(1, :), w3d1(2, :), w3d1(3, :), '*')

    rtx = [getRtFromRES([0.1, 0.2, 0.3, 10, 20, 30]); 0 0 0 1 ];
    w3d2 = rtx * w3d1;

    w3d2 = w3d2 + noise_level * addnoise(w3d2);    
    figure, plot3(w3d2(1, :), w3d2(2, :), w3d2(3, :), '*')
end

% @author       :       zhyh2010
% @date         :       20150806
% @output       :       
% @description  :       add noise

function [noise_new] = addnoise(x1)
    noise = rand(size(x1, 1), size(x1, 2));
    noise_mean = mean(noise, 2);
    noise_std = std(noise, 1, 2);
    noise_new = (noise - repmat(noise_mean, [1 size(x1, 2)])) ./ repmat(noise_std, [1 size(x1, 2)]);
    noise_new_mean = mean(noise_new , 2);
    noise_new_std = std(noise_new, 1, 2);
    assert(all(abs(noise_new_mean) < 1e-6), 'noise did not normalized!!!')
    assert(all(abs(noise_new_std - 1) < 1e-6), 'noise did not normalized!!!')
end

3.3 getRtFromRES

使用欧拉角对 RT 进行描述

function [ Rt ] = getRtFromRES( res )
x = res(1);
y = res(2);
z = res(3);
t1 = res(4);
t2 = res(5);
t3 = res(6);

Rt = [cos(y)*cos(z)-sin(x)*sin(y)*sin(z), -cos(x)*sin(z), sin(y)*cos(z)+sin(x)*cos(y)*sin(z), t1
    cos(y)*sin(z)+sin(x)*sin(y)*cos(z), cos(x)*cos(z), sin(y)*sin(z)-sin(x)*cos(y)*cos(z), t2
    -cos(x)*sin(y), sin(x), cos(x)*cos(y), t3];
end

3.4 RTx_youhua

优化的目标方程， 最小化变换前后的三维点之间的误差

$$minarg || W_2 - RT * W_1 ||$$

function [err] = RTx_youhua(x, w1, w2)
    rtx = [getRtFromRES(x); 0 0 0 1 ];
    w2_c = rtx * w1;
    err = abs(w2_c - w2);
end

3.5 getRESFromRt

function [ res,err ] = getRESFromRt( Rt )
a = real(asin(Rt(3,2)));
b = real(asin(-Rt(3,1)/cos(a)));
c = real(asin(-Rt(1,2)/cos(a)));

res = [a,b,c,Rt(1:3,end)'];
fun = @(res)ce(Rt,res);
[res , ~] = lsqnonlin(fun, res, [], [], optimset('LargeScale','off','Display','off','TolFun',1e-30,...
    'TolX',1e-35,'Algorithm','levenberg-marquardt','MaxFunEvals',1e+100,'MaxIter',1000));
err = ce(Rt,res);

end

function err = ce(Rt,res)
x = res(1);
y = res(2);
z = res(3);
t1 = res(4);
t2 = res(5);
t3 = res(6);

Rt2 = [cos(y)*cos(z)-sin(x)*sin(y)*sin(z) -cos(x)*sin(z) sin(y)*cos(z)+sin(x)*cos(y)*sin(z) t1
    cos(y)*sin(z)+sin(x)*sin(y)*cos(z) cos(x)*cos(z) sin(y)*sin(z)-sin(x)*cos(y)*cos(z) t2
    -cos(x)*sin(y) sin(x) cos(x)*cos(y) t3];

err = Rt2-Rt(1:3, :);
end

4. C++ 版本代码

4.1 项目工程代码

https://code.csdn.net/zhyh1435589631/calcguangbiballcenter/tree/master

4.2 LM优化部分

其实这部分代码中最核心的就是这个LM算法了https://en.wikipedia.org/wiki/Levenberg%E2%80%93Marquardt_algorithm
对照着上面维基百科中的描述，我们可以给出如下实现代码，当然也可以选择使用现有的实现框架等

// levenberg-marquardt法
void CComputeBallCenterFrom2W3dPoints::LM_RTxFrom2W3dPoints(const cv::Mat & w3d1, const cv::Mat & w3d2, cv::Mat & res, double err_thresh)
    Mat err, Jacobi, step, err_0, Jacobi_pinv, step_len;
    int num = 0;
    double uk = 0.15;
    double v = 5;
    Mat J1;
    double err_last_loop = 99999;
    do
        getErrAndJacobiForNewton(w3d1, w3d2, res, err, Jacobi);

        J1 = Jacobi.t()*Jacobi + uk*Mat::eye(Size(Jacobi.cols, Jacobi.cols), CV_64F);
        invert(J1, Jacobi_pinv, DECOMP_SVD);
        Jacobi_pinv = Jacobi_pinv*Jacobi.t();
        step = Jacobi_pinv*err;
        reduce(abs(err), err_0, 0, CV_REDUCE_AVG);
        if (err_0.at<double>(0, 0) < err_last_loop)
            uk = uk / v;
        
        else
            uk = uk * v;
        
        err_last_loop = err_0.at<double>(0, 0);

        reduce(abs(step), step_len, 0, CV_REDUCE_AVG);
        cout << step_len.at<double>(0, 0) << endl;
        if (step_len.at<double>(0, 0) < err_thresh)
            break;
        
        res = res - step.t();
     while (++num < 500);

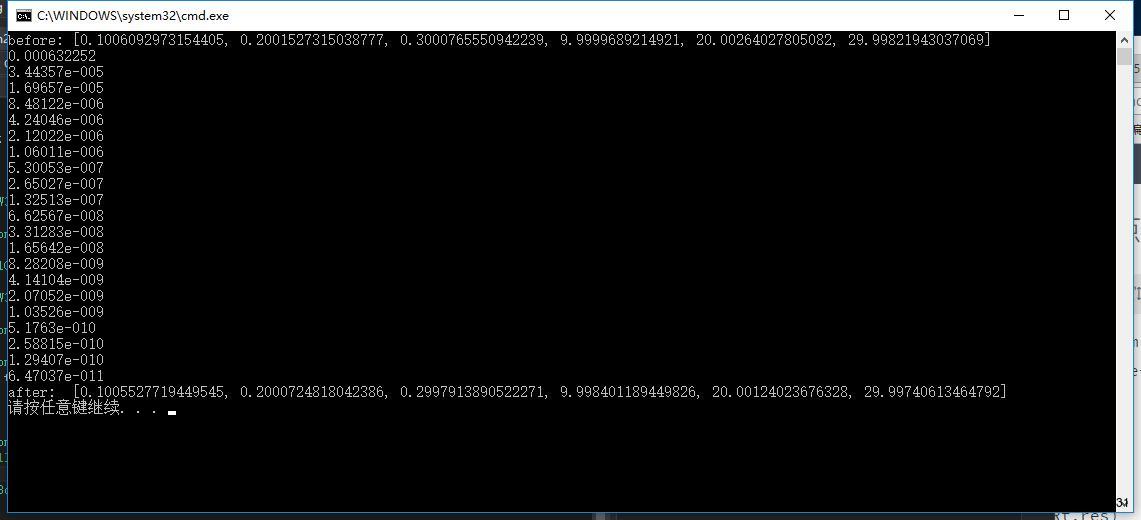
理论值是【0.1， 0.2， 0.3， 10， 20， 30】
由于加入了0.01mm的物点误差，
相应的matlab版本给出的结果为：