重温基础算法内部排序之希尔排序法

Posted 2022-09-07 顧棟

内部排序之希尔排序法

文章目录

• 内部排序之希尔排序法
• • 主要思想
  • 过程演示
  • JAVA代码
  • 算法分析

希尔排序(Shell Sort)是插入排序的一种，它是针对直接插入排序算法的改进。

主要思想

通过根据一定距离将元素分组，同组类的元素来进行，各趟比较所用的距离随着算法的进行而减小，直到只比较相邻元素的最后一趟（距离1）排序为止（最后走一遍直接插入排序，此时已经降低直接插入排序的比较和交换）。希尔的想法是，间距的初始值h=length/2，最后的一个间距值就是1。取值范围就是$length/2，length/2/2，...，1$

过程演示

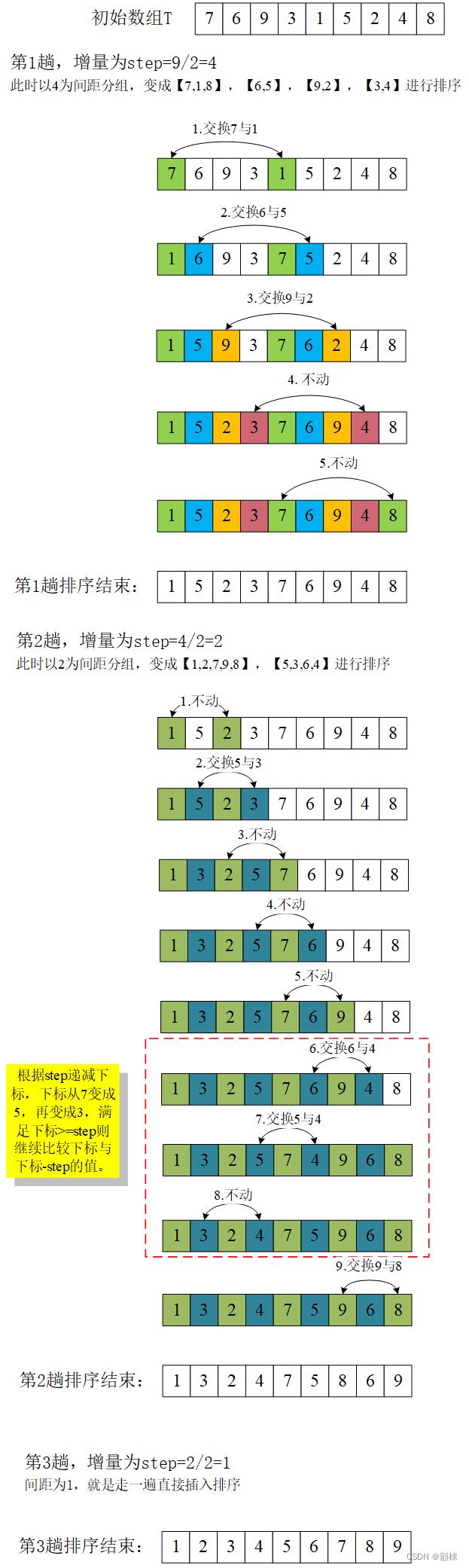
JAVA代码

希尔的增量序列，长度减半的方式， $k,\frac{k}{2},\frac{k}{4}...1,且k=\lfloor \frac{length}{2}\rfloor$。

package sort;

public class ShellSort 
    public static void main(String[] args) 
        int[] o = 7, 6, 9, 3, 1, 5, 2, 4, 8;
        System.out.print("排序前: ");
        for (int t : o) 
            System.out.print(t);
            System.out.print(" ");
        
        System.out.println();


        // 算法部分
        int i, j, step;
        int temp;
        for (step = o.length / 2; step > 0; step /= 2) 
            for (i = step; i < o.length; i++) 
                temp = o[i];
                for (j = i; j >= step; j -= step) 
                    if (temp < o[j - step]) 
                        o[j] = o[j - step];
                     else 
                        break;
                    
                
                o[j] = temp;
            
            System.out.print("step为[" + step + "]排序后: ");
            for (int t : o) 
                System.out.print(t);
                System.out.print(" ");
            
            System.out.println();
        

        System.out.print("最终排序后: ");
        for (int t : o) 
            System.out.print(t);
            System.out.print(" ");
        
        System.out.println();
    

Hibbard增量方式，$2^k-1,2^{k-1}-1,2^{k-2}-\mathrm{1...1},且k\le \lfloor lo{g}_{2}n\rfloor$。

package sort;

public class ShellSort 
    public static void main(String[] args) 

        int[] o = 4, 8, 9, 7, 6, 2, 6, 1;
        System.out.print("排序前: ");
        for (int t : o) 
            System.out.print(t);
            System.out.print(" ");
        
        System.out.println();

        // 算法部分
        int i, j, step;
        int temp;
        int k = (int) Math.floor(Math.log10(o.length) / Math.log10(2));
        for (step = (int) Math.pow(2, k) - 1; step > 0; k -= 1, step = (int) Math.pow(2, k) - 1) 
            for (i = step; i < o.length; i++) 
                temp = o[i];
                for (j = i; j >= step; j -= step) 
                    if (temp < o[j - step]) 
                        o[j] = o[j - step];
                     else 
                        break;
                    
                
                o[j] = temp;
            
            System.out.print("step为[" + step + "]排序后: ");
            for (int t : o) 
                System.out.print(t);
                System.out.print(" ");
            
            System.out.println();
        

        System.out.print("最终排序后: ");
        for (int t : o) 
            System.out.print(t);
            System.out.print(" ");
        
        System.out.println();
    

算法分析

空间复杂度$O(1)$

根据不同的增量序列可以得到不同的时间复杂度。

时间复杂度 使用希尔的增量序列 $k,\frac{k}{2},\frac{k}{4}...1,且k=\lfloor \frac{length}{2}\rfloor$，时间复杂度为$O(n^2)$。

Hibbard增量序列$2^k-1,2^{k-1}-1,2^{k-2}-\mathrm{1...1},且k\le \lfloor lo{g}_{2}n\rfloor$，时间复杂度为$O(n^{3/2})$。