重温基础算法内部排序之基数排序法

Posted 2022-09-24 顧棟

内部排序之基数排序法

文章目录

• 内部排序之基数排序法
• • 主要思想
  • 过程演示
  • java实现
  • 算法分析

基数排序是一种借助多关键字排序的思想对单逻辑关键字进行排序的方法。

一般情况下，假如有$n$个记录的序列
$$R_1,R_2,...,R_n$$
且每个记录$R_i$中含有$d$个关键字$(k_i^0,k_i^1,...,k_i^{d-1})$，则称序列对关键字$K^0,K^1,K^2,...,K^{d-1}$有序指的是：对于序列中任意两个记录$R_i$和$R_j(1\le i\le j\le n)$都满足下列有序关系：
$$(K_i^0,K_i^1,...,K_i^{d-1})<(K_j^0,K_j^0,...,K_j^{d-1})$$
其中$K^0$称为最主位关键字，$K^{d-1}$称为最次位关键字。为了实现多关键字排序，会采用两个方法最高位优先法(MSD)和最低位优先法(LSD)。

主要思想

最高位优先法：

先对最主为关键字$K^0$进行排序，按照相同的$K^0$关键字，将序列拆分成不同的子序列，在对每个子序列的$k^1$进行排序，按$K^1$值的不同在上次拆分的基础上，再次拆分子序列，依次重复，直至对$K^{d-2}$进行排序后，得到的每一个子序列的中都拥有相同的关键字$(K^0,K^1,...,K^{d-2})$，而后在分别每个子序列对$K^{d-1}$进行排序，最后将所有子序列依次连接在一起成为一个有序序列。

最低位优先法：

从最次位关键字$K^{d-1}$进行排序，在对高一位的关键字进行排序，依次重复，直至对$K^0$进行排序后便成为一个有序序列。

过程演示

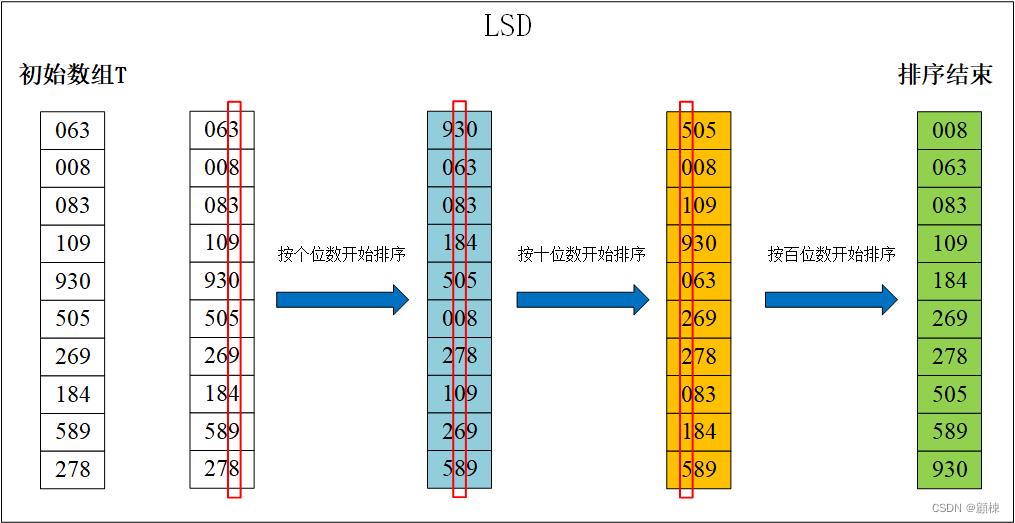
LSD+计数排序动画

java实现

LSD+计数排序实现

package sort;

import java.util.Arrays;

public class RadixSort 

    private static int getMaxValue(int[] arr) 
        int maxValue = arr[0];
        for (int value : arr) 
            if (maxValue < value) 
                maxValue = value;
            
        
        return maxValue;
    

    protected static int getNumLength(long num) 
        if (num == 0) 
            return 1;
        
        int lenght = 0;
        for (long temp = num; temp != 0; temp /= 10) 
            lenght++;
        
        return lenght;
    

    private static int getMaxDigit(int[] arr) 
        int maxValue = getMaxValue(arr);
        return getNumLength(maxValue);
    

    private static int[] arrayAppend(int[] arr, int value) 
        arr = Arrays.copyOf(arr, arr.length + 1);
        arr[arr.length - 1] = value;
        return arr;
    

    public static void main(String[] args) 
        System.out.println(184 % 10);

        int[] o = 63, 8, 83, 109, 930, 505, 269, 184, 589, 278;
        System.out.print("排序前: ");
        for (int t : o) 
            System.out.print(t);
            System.out.print(" ");
        
        System.out.println();

        // 算法部分
        // 十进制的数字
        int mod = 10;
        int dev = 1;
        // 获取最高位数(最大值是几位数)
        int maxDigit = getMaxDigit(o);
        System.out.println("最大值是几位数: " + maxDigit);
        for (int i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) 
            // 考虑负数的情况，这里扩展一倍队列数，其中 [0-9]对应负数，[10-19]对应正数 (bucket + 10)
            int[][] counter = new int[mod * 2][0];

            for (int k : o) 
                // 计算元素应该的下标
                int bucket = k % mod / dev + mod;
                counter[bucket] = arrayAppend(counter[bucket], k);
            

            int index = 0;
            for (int[] bucket : counter) 
                for (int value : bucket) 
                    o[index++] = value;
                
            
        

        System.out.print("排序后: ");
        for (int t : o) 
            System.out.print(t);
            System.out.print(" ");
        
        System.out.println();
    

结果

排序前: 63 8 83 109 930 505 269 184 589 278 
最大值是几位数: 3
排序后: 8 63 83 109 184 269 278 505 589 930 

算法分析

一组序列有$n$个记录，每个记录包含$d$个关键字，每个关键字的取值范围为$rd$个。每一趟分配的时间复杂度是$O(n)$，每一趟收集的时间复杂度是$O(rd)$，整个排序需要$d$趟。总体的时间复杂度就是$O(d(n+rd))$，空间复杂负责度就是$O(rd)$。

概念采用：

《数据结构 （C语言版）》 严蔚敏