剑指offer---Day5

Posted 2022-08-16 Recently 祝祝

Day5:剑指 Offer 14- I. 剪绳子

力扣链接：剑指 Offer 14- I. 剪绳子
题目：给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]…k[m-1] 。请问 k[0]k[1]…*k[m-1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

题解：根据均等切割，可以得出需要让x1与x2尽量相等，尽可能相等时得到的数时最大的分析可以得出。n=2时，只能切成1X1，n=3时切成1X2。无论怎么分，不可能切成1，尽可能切分成2,3,4的数相乘，根据下边的公式2,和4是不能同时存在的，尽可能切成3可以得到更大的数，可以得到最大的乘积，根据余数可以判断是否需要把余数相加边变成4，若余数为1，就利用1 与前一个3相加变成4可以得到更大的乘积。

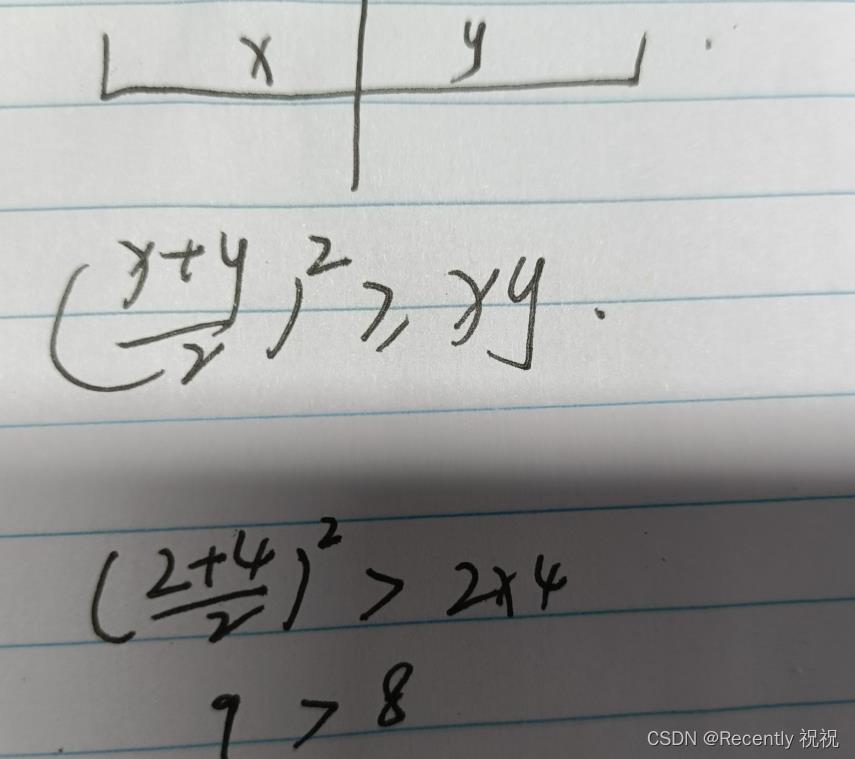
class Solution 
     public int cuttingRope(int n) 
        if(n<=2)
            return 1;
        
        if(n==3)
            return 2;
        
        int res = n/3;
        int mod = n%3;

        if(mod == 0)
            return (int)Math.pow(3,res);
        else if(mod ==1)
            return  (int)Math.pow(3,res-1)*4;
        else
            return  (int)Math.pow(3,res)*2;
        
    

Day5:剑指 Offer 14- II. 剪绳子 II

力扣链接：剑指 Offer 14- II. 剪绳子 II
题目：给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]…k[m - 1] 。请问 k[0]k[1]…*k[m - 1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

题解：数值太大int类型可能会导致栈溢出，所以再获得乘积的时候需要转换为long类型，取余后转换为int类型，一个数与一个比自己大的数取余，无论取多少次余数都还是自己。

class Solution 
    public int cuttingRope(int n) 
        if(n<=2)
            return 1;
        
        if(n==3)
            return 2;
        

        int res = n/3;
        int mod =n%3;
        int p =1000000007;
        if(mod==0)
            return (int) (pow(3,res));
        else if(mod==1)
            return (int)(pow(3,res-1)*4%p);
        else
             return (int)(pow(3,res)*2%p);
        
        //多个数相乘的时候如何取余
    
      long pow(int a, int n)
        long res = 1;
        int p = 1000000007;
        for(int i= 1; i <= n; i++)
            res = (res * a) % p;
        

        return res;
    

Day5:剑指 Offer 15. 二进制中1的个数

力扣链接：剑指 Offer 15. 二进制中1的个数

题目：编写一个函数，输入是一个无符号整数（以二进制串的形式），返回其二进制表达式中数字位数为 ‘1’ 的个数（也被称为 汉明重量).）。

题解：java中& 与符号，二进制与比自己小1的数相与会进行进位，每次相与都能抵消掉一位1，直到n为0结束循环，就能得出有几位1；
也可以使用n与1相与，每次相与之后无符号又移一位，java无符号位移>>>
解1：

public class Solution 
    // you need to treat n as an unsigned value
	    public int hammingWeight(int n) 
	        int res=0;
	        while(n!=0)
	            n&=n-1;
	           res++; 
	    
	    return res;
	

解2：

public class Solution 
    // you need to treat n as an unsigned value
        public int hammingWeight(int n) 
            int res=0;
            while(n!=0)
            res+=n&1; 
            n>>>=1;
        
        return res;
    

Day5:剑指 Offer 16. 数值的整数次方

力扣链接：剑指 Offer 16. 数值的整数次方

题目：实现 pow(x, n) ，即计算 x 的 n 次幂函数（即，xn）。不得使用库函数，同时不需要考虑大数问题。

题解：减少遍历次数，减少运行时间，解析遍历n=13，就可以解析为1+4+8=13,变成三次遍历，重复使用前边的乘积

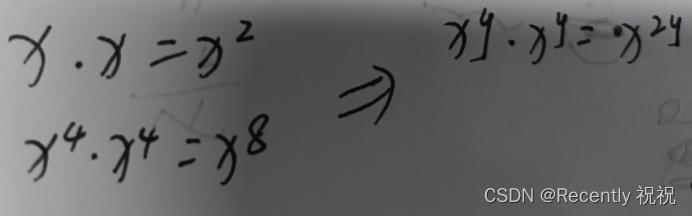
class Solution 
    public double myPow(double x, int n) 
        double res =1;
        long y=n;
        if(n<0)
            y=-y;
            x=1/x;
        
        while(y>0)
           if(y%2==1)
               res=res*x;
           
           x=x*x;
           y=y/2;
        
        return res;
    

end》》》
重要的不是被给予了什么，而是如何去利用被给予的东西。合理化利用资源。