基于多种群机制的PSO算法(优化与探索三 *混合种群思想优化多种群与广义PSO求解JSP)
Posted Huterox
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基于多种群机制的PSO算法(优化与探索三 *混合种群思想优化多种群与广义PSO求解JSP)相关的知识,希望对你有一定的参考价值。
文章目录
前言
本来今天是想要继续研究研究多种群的,但是怎么说心累,于是就想到先找到一个问题,来看看做优化。
然后也是,想到先前被同学点了一下,仔细思考了一下如何用PSO解决这种非连续性,带有序号的问题?所以今天做了两件事。
版权
郑重提示:本文版权归本人所有,任何人不得抄袭,搬运,使用需征得本人同意!
2022.6.22
日期:2022.6.22 DAY 3
混合PSO优化
原来我一直是采用这个方程来做速度更新的,也就是参考一篇好老的文献。
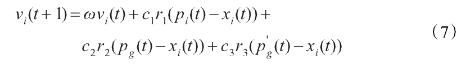
但是效果并不是很理想,不过在高纬度下还可以和最基础的PSO有更好一点的优势,而且运算量只是大了一点。
所以这里也是不知道哪里看到了一篇文章,无意中一撇。于是我继续采用原来的速度方程,然后,这样一改。

也就是速度更新方程变了
def ComputeV(self,bird):
#这个方法是用来计算速度滴
NewV=[]
for i in range(DIM):
# if(self.rand()<0.05):
# v = bird.V[i]*self.W + C1*self.Random()*(bird.PBestX[i]-bird.X[i])\\
# +C2*self.Random()*(bird.GBestX[i]-bird.X[i])\\
# + C3*self.Random()*(bird.CBestX[i]-bird.X[i])
# else:
# v = bird.V[i] * self.W + C1 * self.Random() * (bird.PBestX[i] - bird.X[i]) \\
# + C2 * self.Random() * (bird.GBestX[i] - bird.X[i])
# #这里注意判断是否超出了范围
v1 = bird.V[i] * self.W + C1 * self.Random() * (bird.PBestX[i] - bird.X[i]) \\
+ C2 * self.Random() * (bird.GBestX[i] - bird.X[i])
v2 = bird.V[i] * self.W + C1 * self.Random() * (bird.PBestX[i] - bird.X[i]) \\
+ C2 * self.Random() * (bird.CBestX[i] - bird.X[i])
v = v1*self.miu+(1-self.miu)*v2
if(v>V_max):
v = V_max
elif(v<V_min):
v = V_min
NewV.append(v)
return NewV
对比
我这里还是拿,原来直接分子种群的来做的。
于是同样的参数配置下(除了self.miu这个系数)
现在的:

基础的:

效果上更好。
猜想
其实粒子群的毛病是收敛快,但是都是往一个点跑的,所以快但是容易走到局部最优,因为他是每一步都走最好的,虽然有个体最好的在哪里拉着这个例子,但是全局最好的其实就在个体最好的里面,也就是说,个体最好的速度方向其实和当前迭代下可能的局部最优的方向是一样的,只是这个局部的范围较大。所以如果采用一定的比例降低对Pbest,Gbest的依赖,并且也依赖与小范围内的最优解,这样的话就会出现,局部最好的速度方向,和全局(当前)最好的速度方向不一定一致,这样一来,粒子将有更大的机会是往那一个范围走,而不是往那一个点走,在保证全局搜索能力的同时,还可以避免局部优解。
完整代码
#coding=utf-8
#这个算法是打算在BasePso的基础上,做一个简单的多种群优化
import sys
import os
sys.path.append(os.path.abspath(os.path.dirname(os.getcwd())))
from ONEPSO.BasePso import BasePso
from ONEPSO.Config import *
from ONEPSO.Bird import Bird
import time
import random
class MPSOSimple(BasePso):
rand = random.random
miu = 0.4
def __init__(self):
super(MPSOSimple,self).__init__()
self.Divide()
def Divide(self):
#先来一个最简单的方法,硬分类
CID = 0
for bird in self.Population:
bird.CID=CID
if(bird.ID % ClusterSize==0):
if(CID<=ClusterNumber):
CID+=1
def ComputeV(self,bird):
#这个方法是用来计算速度滴
NewV=[]
for i in range(DIM):
# if(self.rand()<0.05):
# v = bird.V[i]*self.W + C1*self.Random()*(bird.PBestX[i]-bird.X[i])\\
# +C2*self.Random()*(bird.GBestX[i]-bird.X[i])\\
# + C3*self.Random()*(bird.CBestX[i]-bird.X[i])
# else:
# v = bird.V[i] * self.W + C1 * self.Random() * (bird.PBestX[i] - bird.X[i]) \\
# + C2 * self.Random() * (bird.GBestX[i] - bird.X[i])
# #这里注意判断是否超出了范围
v1 = bird.V[i] * self.W + C1 * self.Random() * (bird.PBestX[i] - bird.X[i]) \\
+ C2 * self.Random() * (bird.GBestX[i] - bird.X[i])
v2 = bird.V[i] * self.W + C1 * self.Random() * (bird.PBestX[i] - bird.X[i]) \\
+ C2 * self.Random() * (bird.CBestX[i] - bird.X[i])
v = v1*self.miu+(1-self.miu)*v2
if(v>V_max):
v = V_max
elif(v<V_min):
v = V_min
NewV.append(v)
return NewV
def ComputeX(self,bird):
NewX = []
NewV = self.ComputeV(bird)
bird.V = NewV
for i in range(DIM):
x = bird.X[i]+NewV[i]
if (x > X_up):
x = X_up
elif (x < X_down):
x = X_down
NewX.append(x)
return NewX
def InitPopulation(self):
#初始化种群
#这个是记录全局最优解的
GBestX = [0. for _ in range(DIM)]
Flag = float("inf")
#还有一个是记录Cluster最优解的
CBest =
CFlag =
for i in range(ClusterNumber):
CFlag[i]=float("inf")
for bird in self.Population:
bird.PBestX = bird.X
bird.Y = self.target.SquareSum(bird.X)
bird.PbestY = bird.Y
bird.CBestX = bird.X
bird.CBestY = bird.Y
if(bird.Y<=Flag):
GBestX = bird.X
Flag = bird.Y
if(bird.Y<=CFlag.get(bird.CID)):
CBest[bird.CID]=bird.X
CFlag[bird.CID] = bird.Y
#便利了一遍我们得到了全局最优的种群
for bird in self.Population:
bird.GBestX = GBestX
bird.GBestY = Flag
bird.CBestY=CFlag.get(bird.CID)
bird.CBestX=CBest.get(bird.CID)
def Running(self):
#这里开始进入迭代运算
for iterate in range(1,IterationsNumber+1):
w = LinearW(iterate)
#这个算的GBestX其实始终是在算下一轮的最好的玩意
GBestX = [0. for _ in range(DIM)]
Flag = float("inf")
CBest =
CFlag =
for i in range(ClusterNumber):
CFlag[i] = float("inf")
for bird in self.Population:
#更改为线性权重
self.W = w
x = self.ComputeX(bird)
y = self.target.SquareSum(x)
# 这里还是要无条件更细的,不然这里的话C1就失效了
# if(y<=bird.Y):
# bird.X = x
# bird.PBestX = x
bird.X = x
bird.Y = y
if(bird.Y<=bird.PbestY):
bird.PBestX=bird.X
bird.PbestY = bird.Y
#个体中的最优一定包含了全局经历过的最优值
if(bird.PbestY<=Flag):
GBestX = bird.PBestX
Flag = bird.PbestY
if (bird.Y <= CFlag.get(bird.CID)):
CBest[bird.CID] = bird.X
CFlag[bird.CID] = bird.Y
for bird in self.Population:
bird.GBestX = GBestX
bird.GBestY=Flag
bird.CBestY = CFlag.get(bird.CID)
bird.CBestX = CBest.get(bird.CID)
if __name__ == '__main__':
start = time.time()
mpso = MPSOSimple()
mpso.InitPopulation()
mpso.Running()
end = time.time()
# for bird in mpso.Population:
# print(bird)
print(mpso.Population[0])
print("花费时长:",end-start)
广义PSO解决JSP问题
JSP问题
JSP问题呢就是作业车间调度问题。这里的话,我就不阐述具体的问题了,因为问题的种类其实很多,我只说我这里的模型。
数据定义
关于这个问题,我们先来看看我们定义的测试数据
import numpy as np
class DataTest(object):
TimeTable = np.array([[3, 6, 5],
[4, 3, 3],
[4, 5, 6],
[4, 3, 3],
[6, 5, 6],
[4, 3, 3],
[7, 8, 7],
[5, 7, 5],
[7, 3, 7],
[6, 4, 4]],
dtype="int32"
)
MechineTable = np.array(
[[2, 1, 3],
[3, 2, 1],
[1, 3, 2],
[2, 3, 1],
[1, 2, 3],
[3, 2, 1],
[3, 1, 2],
[1, 2, 3],
[3, 1, 2],
[2, 1, 3]],
dtype="int32"
)
TimeTable 表示每一个工作的每一个工序所需要的时间,例如表中的第一行[3,6,5]表示,第一个作业,第一道工序需要3,第二个要6,第三要5
MechineTable 表示每一个工作对应的工序需要在那个机器上加工。例如[2,1,3] 表示,第一个工作的第一道工序需要在序号为2的机器上加工,第二道工序需要在1号上加工,以此类推。
约束:工作需要按照工序进行,每台机器只能在同时加工一道工序。
DNA编码
[ 2 4 2 4 1 3 10 6 5 3 6 8 9 8 10 3 10 1 7 9 7 5 8 9 6 5 1 7 4 2]
以刚刚的数据集为例,DNA编码表示执行的顺序。
长度为机器数*工作数
解读:
第一个2 表示第二个工作的第一道工序先执行,然后执行第4个工作的第一道工序,之后执行第二个工作的第一道工序,当出现第二个2时表示第二个工作的第二道工序执行。
具体在哪一个机器上执行,需要查看对应的机器表,例如第一个2,第二个工作的第一个工序执行,查表得到是第三个机器([3,2,1])
广义PSO执行
由于我们无法直接使用速度公式更新,并且对应的也不是连续性的玩意,所以流程如下:
- 初始化化DNA,计算适应值
- 计算出Pbest,Gbest
- 按照一定的策略选择出较好的,合适的粒子
- 让当前粒子与选择出的合适的粒子,按照遗传算法的策略,交叉,变异。产生新的位置,这里是DNA序列。
- 进入循环直到满足条件。
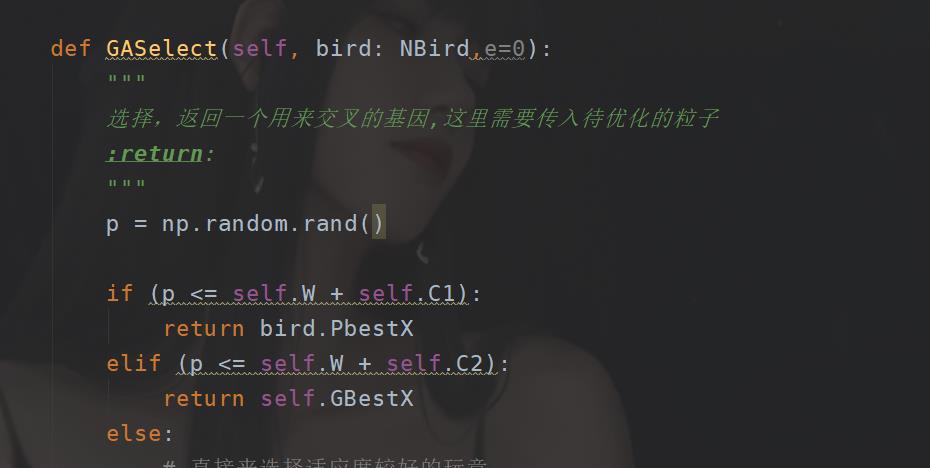
合适的策略选择粒子
这里采用轮盘算法,w,c1,c2表示一种概率。
def GASelect(self, bird: NBird,e=0):
"""
选择,返回一个用来交叉的基因,这里需要传入待优化的粒子
:return:
"""
p = np.random.rand()
if (p <= self.W + self.C1):
return bird.PbestX
elif (p <= self.W + self.C2):
return self.GBestX
else:
# 直接来选择适应度较好的玩意
weight = np.array([bird.Fitness for bird in self.Population])
weight = ((weight.max() - weight )/(weight.max()-weight.min()))
weight = (weight/weight.sum())
index_ = np.random.choice(np.arange(0, self.size), size=1, p=weight)[0]
greatbird = self.Population[index_]
# if(self.Fintess(greatbird)>bird.Fitness):
# greatbird = bird.X
# else:
# greatbird = greatbird.X
return greatbird.X
这里是如果满足第一个概率,那么直接选择Pbest,满足第二个给Gbest,第三个就直接使用异常的策略。
对比
优点:具备快速搜索能力,同时由于多种策略,自带扰动,可以让解较为均匀,相对于GA,可以快速求解,并且在近10轮测试当中,GA 有4次未得到最优解,得到优解平均在20+次迭代(按照6轮算)
当然由于两者参数的区别多少是有差异的。
PSO均得到,最快在第6次达到最优解,平均10+次迭代。
缺点(低情商):可以得到最优的,但是粒子总体在一个范围内,不在一个点上。
优点(高情商):粒子分布在一个区域内,解多样性。
完整编码
import numpy as np
import random
from ONEPSO.DataTest import DataTest
class NBird(object):
ID = None
PbestX = None
PFitness = None
Fitness = None
# 按照顺序是机器1,2,3上面工序1,2,3的加工时间
Times = None
# 表示加工的顺序
Mechines = None
X = None
def __init__(self, ID):
self.ID = ID
class PSO_JSP:
GBestX = None
GFitness = float("inf")
BID = 0
C1 = 0.2 # 个体学习
C2 = 0.3 # 群体学习
W = 0.4
BianYan = 0.1
works = 10
mechine = 3
Population = []
dataTest = DataTest()
def __init__(self, size, epoch):
self.size = size
self.epoch = epoch
self.Population = [NBird(ID) for ID in range(1, self.size + 1)]
for bird in self.Population:
# 这里初始化种群,生成DNA
# times = np.random.choice(np.arange(3,9), size=self.mechine)
# mechines = np.random.choice(np.arange(1,self.mechine+1), size=self.mechine, replace=False)
# bird.Times=times
# bird.Mechines=mechines
bird.Times = self.dataTest.TimeTable
bird.Mechines = self.dataTest.MechineTable
self.__CreateDNA(bird)
def __CreateDNA(self, bird: NBird):
nums = np.ones(self.works)
temp = []
for j in range(self.works * self.mechine):
num = random.randint(1, self.works)
while (nums[num - 1] > self.mechine):
num = random.randint(1, self.works)
nums[num - 1] += 1
temp.append(num)
bird.X = temp
def Init_PSOJSP(self, Population):
"""
这个是初始化PSO,便于后面的交叉变异遗传...
:param Population:
:return: None
"""
for bird in self.Population:
bird.PbestX = bird.X
bird.Fitness = self.Fintess(bird)
bird.PFitness = bird.Fitness
if (bird.Fitness <= self.GFitness):
self.GFitness = bird.Fitness
self.GBestX = bird.X
self.BID = bird.ID
def GAStrategy(self, bird: NBird, greatbird: np.array):
# 这个采用GA策略,交叉,变异,并且在这里进行验证
left, right = np.random.choice(self.works * self.mechine, 2,replace=False)
if left > right:
left, right = right, left
father, mother = bird.X, greatbird
child = np.array([0 for _ in range(len(father))])
nums = np.zeros(self.works)
for j in range(left, right + 1):
child[j] = father[j]
nums[child[j] - 1] 以上是关于基于多种群机制的PSO算法(优化与探索三 *混合种群思想优化多种群与广义PSO求解JSP)的主要内容,如果未能解决你的问题,请参考以下文章
TSP问题基于混合粒子群算法求解旅行商问题matlab源码含GUI
优化调度基于matlab多目标粒子群算法求解风电光伏储能电网发电与需求响应调度优化问题含Matlab源码 239期