基于多种群机制的PSO算法Python实现
Posted Huterox
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基于多种群机制的PSO算法Python实现相关的知识,希望对你有一定的参考价值。
文章目录
前言
当前还是正对单目标算法的优化,目的是为了能够避免由于单目标算法本身的局限性导致多目标的效果骤降。
本次代码采用Python实现,后期将转移至Flink 平台。
版权
郑重提示:本文版权归本人所有,任何人不得抄袭,搬运,使用需征得本人同意!
参考文献
[1]廖延娜,李梦君,张婧琪.K均值聚类-粒子群优化多目标定位算法[J].电子设计工程,2018,26(02):56-60.
摘要:针对复杂图像背景下的多目标定位问题,采用K均值聚类-粒子群优化联合算法,应用排挤机制确定初始聚类质心;根据特征向量将目标粒子种群分为若干个子群,在每个目标子群中进行粒子优化更新;重复进行聚类和子群优化,直到各个目标子群得到最优解。将该算法运用到多车牌定位中,在实际采集大量停车场图片的基础上,设计了车牌目标粒子模型,特征向量和适应度函数,进行了算法的Matlab仿真。实验结果表明:K均值聚类-粒子群优化实现了多个目标的准确自动定位,算法稳定收敛。
[2]郭成,张万达,王波,王加富.多种群并行协作的粒子群算法[J].计算机与现代化,2022,(01):33-40.
摘要:针对高维复杂优化问题在求解时容易产生维数灾难导致算法极易陷入局部最优的问题,提出一种能够综合考虑高维复杂优化问题的特性,动态调整进化策略的多种群并行协作的粒子群算法。该算法在分析高维复杂问题求解过程中的粒子特点的基础上,建立融合环形拓扑、全连接形拓扑和冯诺依曼拓扑结构的粒子群算法的多种群并行协作的网络模型。该模型结合3种拓扑结构的粒子群算法在解决高维复杂优化问题时的优点,设计一种基于多群落粒子广播-反馈的动态进化策略及其进化算法,实现高维复杂优化环境中拓扑的动态适应,使算法在求解高维单峰函数和多峰函数时均具有较强的搜索能力。仿真结果表明,该算法在求解高维复杂优化问题的寻优精度和收敛速度方面均有良好的性能。
[3]罗德相,周永权,黄华娟,韦杏琼.多种群粒子群优化算法[J].计算机工程与应用,2010,46(19):51-54.
摘要:将一定规模的粒子群平分成三个子群,并分别按基本粒子优化算法、ω自线性调整策略的粒子群算法和云自适应粒子群算法三种不同规则进化,既保持各个子群和算法的独立性和优越性,又不增加算法的复杂性,并提出"超社会"部分,重新定义了速度更换式子,同时还引入了扩张变异方法和扰动操作。实验仿真结果表明,给出算法的全局搜索能力、收敛速度,精度和稳定性均有了显著提高。
[4]杨道平.粒子群算法邻域拓扑结构研究[J].中国高新技术企业,2009,(16):36-37.
摘要:粒子群算法(PSO算法)是一种启发式全局优化技术。PSO的邻域拓扑结构是决定粒子群优化算法效果的一个很重要的因素,不同邻域拓扑结构的粒子群算法,效果差别很大。文章分析了邻域拓扑结构与PSO算法的关系,阐述了粒子群算法邻域拓扑结构研究现状,提出了未来可能的研究方向。
这里我参考了四篇论文,于是我这里提出了三个优化想法,这里先实现两个版本.
2022.6.20
日期:2022.6.20 DAY 1
第一个点
先基于非矩阵运算实现最基本的PSO算法
第二个点
基于第三个引用实现最简单的算法。这个其实在PSO实现了,但是这个后面我想上强化学习优化,所以还得单独搞成python的。
第一个点实现(基础PSO实现)
ok ,先来看到今天的第一个工作点,传统的最基础的在1995年提出的算法。
整个项目结构如下:

算法的基础核心公式如下:
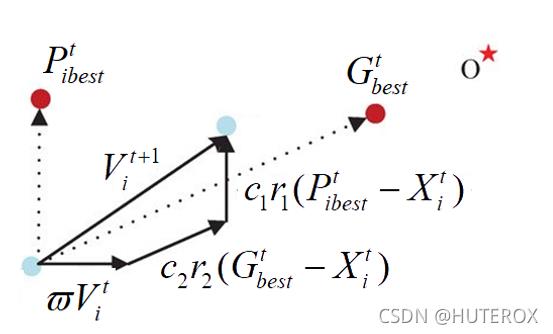

算法配置Config
首先是配置
这个主要负责后面的各种配置,然后我们这边统一是使用线性权重来做的。
# 相关参数的设置通过配置中心完成
C1=2.0
C2=2.0
C3=2.0
W = 0.4
#单目标下定义的维度
DIM = 2
X_down = -2.0
X_up = 2.0
V_min = -4.0
V_max = 4.0
#这个参数是后面优化多种群PSO算法的参数
ClusterSize = 20
ClusterNumber = 3
#种群的大小
PopulationSize = 60
IterationsNumber = 1000
def LinearW(iterate):
#传入迭代次数
Wmax = 0.9
Wmin = 0.4
w = Wmax-(iterate*((Wmax-Wmin)/IterationsNumber))
return w
目标函数Target
之后是我们的目标优化函数,这里的话我也是单独提取出来了,因为我打算先好好优化单目标,然后去优化多目标,之后咱们再找几个实际的点去突破,然后文章就搞出来了,虽然也是有类似PlatEMO 这种平台,但是作为软工本工的大二学子,我还是喜欢自己写轮子,而且我后面还要上Flink,上流处理引擎走分布式(所以后面的代码我不用矩阵,用类,用对象来表示更多的信息,单机无并发,多机可并发,如果是矩阵的话,别想了,很麻烦。
#这个玩意是用来定义需要优化的函数的地方
class Target(object):
def SquareSum(self,X:list):
res = 0
for x in X:
res+=x*x
return res
Bird定义
这个Bird就是我为了减少矩阵运算做的事情
虽然实际上我用numpy会很爽,直接矩阵并行运算,然后更新就行了,但是一单上了流处理,就难搞了,到后面如果搞的话,搞不好还是在一台机子上完成了矩阵运算,如果看Flink处理数据同步的机制的话,矩阵是不好拆分的,然后他是按照最慢的那个来的,如果拆分了,拆多少,怎么合并,延时怎么处理都是问题。
#这里我们使用定义Class的方式实现PSO,便于后面调整
from ONEPSO.Config import *
import random
class Bird(object):
ID = 0
#这个是划分多种群时的种群ID
CID = 0
Iterate = 0
Y = None
X = None
#记录个体的最优值,这个关系到后面求取全局最优值
PbestY = None
PBestX = None
GBestX = None
GBestY = None
CBestY=None
CBestX=None
V = None
def __init__(self,ID):
self.ID = ID
self.V = [random.random() *(V_max-V_min) + V_min for _ in range(DIM)]
self.X = [random.random() *(X_up-X_down) + X_down for _ in range(DIM)]
def __str__(self):
return "ID:"+str(self.ID)+" -Fintess:%.2e:"%(self.Y)+" -X"+str(self.X)+" -PBestFitness:%.2e"%(self.PbestY)+" -PBestX:"+str(self.PBestX)+\\
"\\n -GBestFitness:%.2e"%(self.GBestY)+" -GBestX:"+str(self.GBestX)
基本算法实现
之后是最基本的实现了
#这个是最基础的PSO算法实现,用于测试当前算法架构的合理性
#此外这个玩意还是用来优化的工具类,整个算法是为了求取最小值
from ONEPSO.Bird import Bird
from ONEPSO.Config import *
from ONEPSO.Target import Target
import random
import time
class BasePso(object):
Population = None
Random = random.random
target = Target()
W = W
def __init__(self):
#为了方便,我们这边直接先从1开始
self.Population = [Bird(ID) for ID in range(1,PopulationSize+1)]
def ComputeV(self,bird:Bird):
#这个方法是用来计算速度滴
NewV=[]
for i in range(DIM):
v = bird.V[i]*self.W + C1*self.Random()*(bird.PBestX[i]-bird.X[i])\\
+C2*self.Random()*(bird.GBestX[i]-bird.X[i])
#这里注意判断是否超出了范围
if(v>V_max):
v = V_max
elif(v<V_min):
v = V_min
NewV.append(v)
return NewV
def ComputeX(self,bird:Bird):
NewX = []
NewV = self.ComputeV(bird)
for i in range(DIM):
x = bird.X[i]+NewV[i]
if(x>X_up):
x = X_up
elif(x<X_down):
x = X_down
NewX.append(x)
return NewX
def InitPopulation(self):
#初始化种群
GBestX = [0. for _ in range(DIM)]
Flag = float("inf")
for bird in self.Population:
bird.PBestX = bird.X
bird.Y = self.target.SquareSum(bird.X)
bird.PbestY = bird.Y
if(bird.Y<=Flag):
GBestX = bird.X
Flag = bird.Y
#便利了一遍我们得到了全局最优的种群
for bird in self.Population:
bird.GBestX = GBestX
bird.GBestY = Flag
def Running(self):
#这里开始进入迭代运算
for iterate in range(1,IterationsNumber+1):
w = LinearW(iterate)
#这个算的GBestX其实始终是在算下一轮的最好的玩意
GBestX = [0. for _ in range(DIM)]
Flag = float("inf")
for bird in self.Population:
#更改为线性权重
self.W = w
x = self.ComputeX(bird)
y = self.target.SquareSum(x)
# 这里还是要无条件更细的,不然这里的话C1就失效了
# if(y<=bird.Y):
# bird.X = x
# bird.PBestX = x
bird.X = x
bird.Y = y
if(bird.Y<=bird.PbestY):
bird.PBestX=bird.X
bird.PbestY = bird.Y
#个体中的最优一定包含了全局经历过的最优值
if(bird.PbestY<=Flag):
GBestX = bird.PBestX
Flag = bird.PbestY
for bird in self.Population:
bird.GBestX = GBestX
bird.GBestY=Flag
if __name__ == '__main__':
start = time.time()
basePso = BasePso()
basePso.InitPopulation()
basePso.Running()
end = time.time()
for bird in basePso.Population:
print(bird)
print("花费时长:",end-start)
整个算法写起来是很简单的,而且用这种写法也是最容易理解,最容易修改的,因为很多东西我就可以直接改了。
第二个点实现(参考参考文献三)
之后是我们多种群的。
这个我这里先实现的是最简单的这个,多种群的(其实写这个也就是为了做测试,后面还有三个点要实现),还有几篇文献明天要处理一下。
文章这个东西,看懂了写起代码是真的快。
突然发现在学校实验室混是真爽,不然现在还在CURD,还在八股文捏。
那么这个代码是这样的,分三个小群,现在是直接分,三个组,然后更新方程变成这样

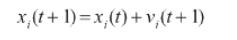
后面的两个点,一个是围绕这个分种群怎么分,一个是围绕这个种群之间如何交互,第一篇就提到了不同拓扑网络的问题。最后一个是如何对参数进行优化,因为这个PSO,你也会发现这个参数对PSO的影响很大,例如C1,2,3的设置,这个意味着你后面会偏向哪一个,这里我考虑用强化学习优化,先来个简单的QL试试水。
#这个算法是打算在BasePso的基础上,做一个简单的多种群优化
from ONEPSO.BasePso import BasePso
from ONEPSO.Config import *
from ONEPSO.Bird import Bird
import time
class MPSOSimple(BasePso):
def __init__(self):
super(MPSOSimple,self).__init__()
self.Divide()
def Divide(self):
#先来一个最简单的方法,硬分类
CID = 0
for bird in self.Population:
bird.CID=CID
if(bird.ID % ClusterSize==0):
if(CID<=ClusterNumber):
CID+=1
def ComputeV(self,bird:Bird):
#这个方法是用来计算速度滴
NewV=[]
for i in range(DIM):
v = bird.V[i]*self.W + C1*self.Random()*(bird.PBestX[i]-bird.X[i])\\
+C2*self.Random()*(bird.GBestX[i]-bird.X[i]) + C3*self.Random()*(bird.CBestX[i]-bird.X[i])
#这里注意判断是否超出了范围
if(v>V_max):
v = V_max
elif(v<V_min):
v = V_min
NewV.append(v)
return NewV
def ComputeX(self,bird:Bird):
NewX = []
NewV = self.ComputeV(bird)
for i in range(DIM):
x = bird.X[i]+NewV[i]
if (x > X_up):
x = X_up
elif (x < X_down):
x = X_down
NewX.append(x)
return NewX
def InitPopulation(self):
#初始化种群
#这个是记录全局最优解的
GBestX = [0. for _ in range(DIM)]
Flag = float("inf")
#还有一个是记录Cluster最优解的
CBest =
CFlag =
for i in range(ClusterNumber):
CFlag[i]=float("inf")
for bird in self.Population:
bird.PBestX = bird.X
bird.Y = self.target.SquareSum(bird.X)
bird.PbestY = bird.Y
bird.CBestX = bird.X
bird.CBestY = bird.Y
if(bird.Y<=Flag):
GBestX = bird.X
Flag = bird.Y
if(bird.Y<=CFlag.get(bird.CID)):
CBest[bird.CID]=bird.X
CFlag[bird.CID] = bird.Y
#便利了一遍我们得到了全局最优的种群
for bird in self.Population:
bird.GBestX = GBestX
bird.GBestY = Flag
bird.CBestY=CFlag.get(bird.CID)
bird.CBestX=CBest.get(bird.CID)
def Running(self):
#这里开始进入迭代运算
for iterate in range(1,IterationsNumber+1):
w = LinearW(iterate)
#这个算的GBestX其实始终是在算下一轮的最好的玩意
GBestX = [0. for _ in range(DIM)]
Flag = float("inf")
CBest =
CFlag =
for i in range(ClusterNumber):
CFlag[i] = float("inf")
for bird in self.Population:
#更改为线性权重
self.W = w
x = self.ComputeX(bird)
y = self.target.SquareSum(x)
# 这里还是要无条件更细的,不然这里的话C1就失效了
# if(y<=bird.Y):
# bird.X = x
# bird.PBestX = x
bird.X = x
bird.Y = y
if(bird.Y<=bird.PbestY):
bird.PBestX=bird.X
bird.PbestY = bird.Y
#个体中的最优一定包含了全局经历过的最优值
if(bird.PbestY<=Flag):
GBestX = bird.PBestX
Flag = bird.PbestY
if (bird.Y <= CFlag.get(bird.CID)):
CBest[bird.CID] = bird.X
CFlag[bird.CID] = bird.Y
for bird in self.Population:
bird.GBestX = GBestX
bird.GBestY=Flag
bird.CBestY = CFlag.get(bird.CID)
bird.CBestX = CBest.get(bird.CID)
if __name__ == '__main__':
start = time.time()
mpso = MPSOSimple()
mpso.InitPopulation()
mpso.Running()
end = time.time()
for bird in mpso.Population:
print(bird)
print("花费时长:",end-start)
对比
这个怎么说呢,后者的效果相对来说还是不错的。

原来的BasePSo

我这个是平均算的哈
以上是关于基于多种群机制的PSO算法Python实现的主要内容,如果未能解决你的问题,请参考以下文章