自动驾驶PID实现轨迹跟踪
Posted CHH3213
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了自动驾驶PID实现轨迹跟踪相关的知识,希望对你有一定的参考价值。
文章目录
参考资料
1. PID控制原理
1.1 基本概念
PID( Proportional Integral Derivative)是工业应用最为广泛 的控制器。学习过控制理论的同学对它一定不陌生(毕竟调参这事可以记一辈子呢~~)。
PID控制器(比例-积分-微分控制器),由比例单元(Proportional)、积分单元(Integral)和微分单元(Derivative)组成。可以透过调整这三个单元的增益 K p K_p Kp, K i K_i Ki和 K d K_d Kd来调定其特性。
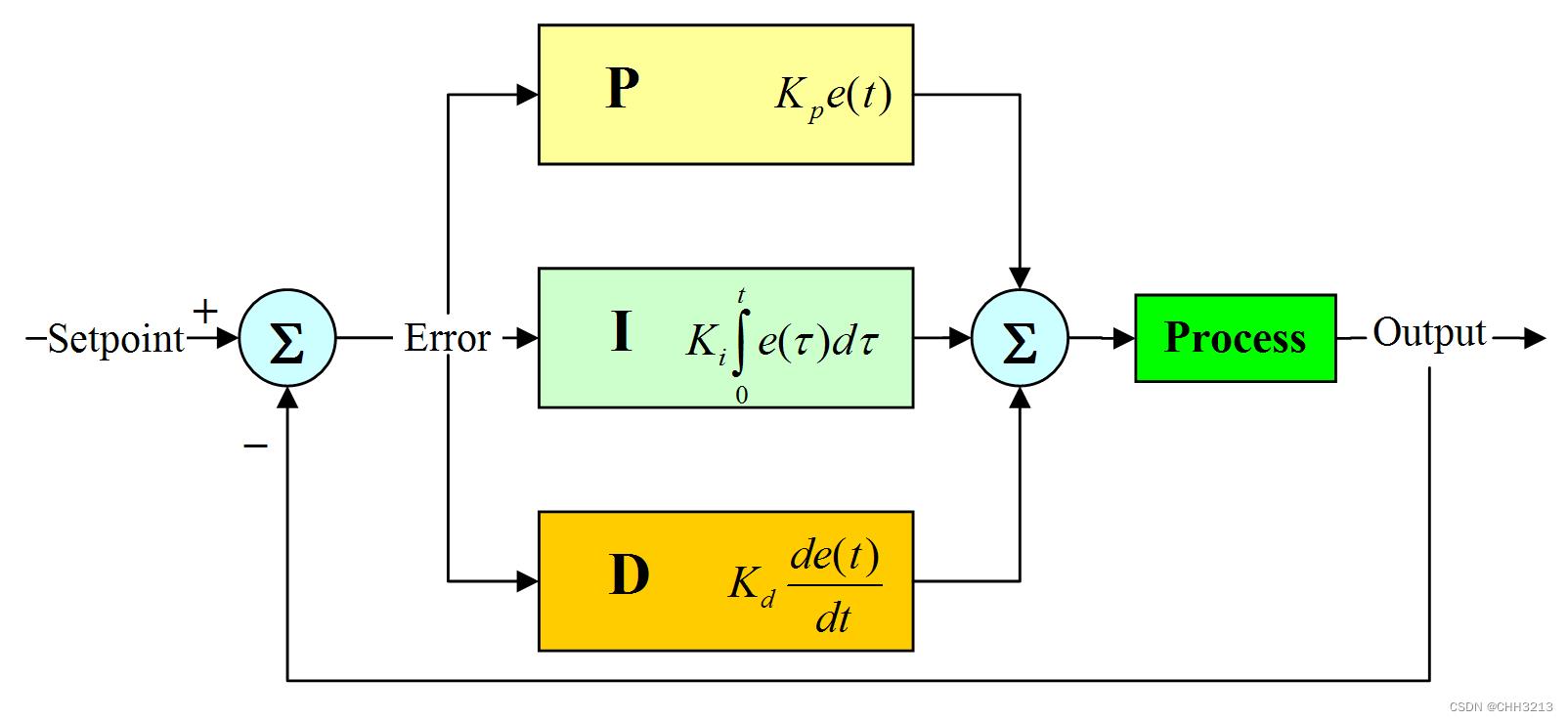
PID算法可以用下式表示:
u
(
t
)
=
K
p
e
(
t
)
+
K
i
∫
0
t
e
(
τ
)
d
τ
+
K
d
d
d
t
e
(
t
)
=
K
p
[
e
(
t
)
+
1
T
i
∫
0
t
e
(
τ
)
d
τ
+
T
d
d
d
t
e
(
t
)
]
(1)
\\tag1 \\beginmatrix \\mathrmu(t)&=K_p e(t)+K_i \\int_0^t e(\\tau) d \\tau+K_d \\fracdd t e(t)\\\\ &=K_p \\left[e(t)+\\frac1T_i\\int_0^t e(\\tau) d \\tau+T_d \\fracdd t e(t)\\right] \\endmatrix
u(t)=Kpe(t)+Ki∫0te(τ)dτ+Kddtde(t)=Kp[e(t)+Ti1∫0te(τ)dτ+Tddtde(t)](1)
其中
- K p K_p Kp : 比例增益,是调适参数
- K i K_i Ki : 积分增益,也是调适参数
- K d K_d Kd : 微分增益,也是调适参数
- T i T_i Ti:积分时间常数
- T d T_d Td:微分时间常数
- e e e : 误差=设定值 ( S P ) − (\\mathrmSP)- (SP)− 当前值( P V ) \\mathrmPV) PV)
- t t t : 当前时间
- τ \\tau τ : 积分变数,数值从 0 到目前时间 t t t
当被控对象的结构和参数不能完全掌握,或得不到精确的数学模型时,控制理论的其它技术难以采用时,系统控制器的结构和参数必须依靠经验和现场调试来确定,这时应用PID控制技术最为方便。即当我们不完全了解一个系统和被控对象,或不能通过有效的测量手段来获得系统参数时,最适合用PID控制技术。
任何闭环控制系统的首要任务是要稳(稳定)、准(准确)、快(快速)的响应命令。PID的主要工作就是如何实现这一任务。
PID控制器的比例单元§、积分单元(I)和微分单元(D)分别对应目前误差、过去累计误差及未来误差。若是不知道受控系统的特性,一般认为PID控制器是最适用的控制器.
-
增大比例环节将加快系统的响应,它的作用于输出值较快,但不能很好稳定在一个理想的数值,不良的结果是虽较能有效的克服扰动的影响,但有余差出现,过大的比例系数会使系统有比较大的超调,并产生振荡,使稳定性变坏。
-
积分环节能在比例的基础上消除余差,它能对稳定后有累积误差的系统进行误差修整,减小稳态误差。
-
微分环节具有超前作用,对于具有容量滞后的控制通道,引入微分参与控制,在微分项设置得当的情况下,对于提高系统的动态性能指标,有着显著效果,它可以使系统超调量减小,减小震荡,稳定性增加,动态误差减小。
在调整的时候,我们要做的任务就是在系统结构允许的情况下,在这三个参数之间权衡调整,达到最佳控制效果,实现稳、准、快的控制特点。
在实际应用中,主要有以下不足:
1. 在实际工业生产过程往往具有非线性、时变不确定,难以建立精确的数学模型,常规的PID控制器不能达到理想的控制效果;
2. 在实际生产现场中,由于受到参数整定方法烦杂的困扰,常规PID控制器参数往往整定不良、效果欠佳,对运行工况的适应能力很差。
1.2 数字 PID 控制算法
在实际计算机实现时,由于计算机控制是一种采样控制, 它只能根据采样时刻的偏差计算控制量,而不能像模拟控制那样连续输出控制量, 进行连续控制,所以实现的是离散形式的PID,即数字PID控制算法
1. 位置式PID
位置式PID是当前系统的实际位置,与你想要达到的预期位置的偏差,进行PID控制
设采样时间为
T
T
T ,公式(1)中的积分项可以用下式近似
∫
0
t
e
(
τ
)
d
τ
=
T
∑
j
=
0
k
e
j
\\int_0^t e(\\tau) d \\tau=T\\sum_j=0^k e_j
∫0te(τ)dτ=Tj=0∑kej
微分项可近似为(后向差分法)
d
e
(
t
)
d
t
=
e
k
−
e
k
−
1
T
\\fracd e\\left(t\\right)d t=\\frace_k-e_k-1T
dtde(t)=Tek−ek−1
故公式(1)化为 以上是关于自动驾驶PID实现轨迹跟踪的主要内容,如果未能解决你的问题,请参考以下文章
u
k
=
K
p
e
k
+
T
T
i
∑
j
=
0
k
e
j
+
T
d
T
[
e
k
−
e
k
−
1
]
=
K
p
e
k
+
K
i
∑
j
=
0
k
e
j
+
K
d
[
e
k
−
e
k
−
1
]
(2)
\\tag2 \\beginmatrix u_k&=K_p\\left\\e_k+\\fracTT_i \\sum_j=0^k e_j+\\fracT_dT[e_k-e_k-1]\\right\\\\\\ &=K_p e_k+K_i \\sum_j=0^k e_j+K_d[e_k-e_k-1] \\endmatrix
uk=Kpek+TiT∑j=0kej+TTd[ek−ek−1]=Kpek+Ki∑j=0kej+Kd[ek−e