图论刷题-3力扣 733. 图像渲染
Posted smile-yan
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了图论刷题-3力扣 733. 图像渲染相关的知识,希望对你有一定的参考价值。
733. 图像渲染
力扣原题 地址
难度与标签
中等难度
- 广度优先搜索(BFS)
- 深度优先搜索(DFS)
题目描述
有一幅以二维整数数组表示的图画,每一个整数表示该图画的像素值大小,数值在 0 到 65535 之间。
给你一个坐标 (sr, sc) 表示图像渲染开始的像素值(行 ,列)和一个新的颜色值 newColor,让你重新上色这幅图像。
为了完成上色工作,从初始坐标开始,记录初始坐标的上下左右四个方向上像素值与初始坐标相同的相连像素点,接着再记录这四个方向上符合条件的像素点与他们对应四个方向上像素值与初始坐标相同的相连像素点,……,重复该过程。将所有有记录的像素点的颜色值改为新的颜色值。
最后返回经过上色渲染后的图像。
示例 1:
输入:
image = [[1,1,1],[1,1,0],[1,0,1]]
sr = 1, sc = 1, newColor = 2
输出: [[2,2,2],[2,2,0],[2,0,1]]
解析:
在图像的正中间,(坐标(sr,sc)=(1,1)),
在路径上所有符合条件的像素点的颜色都被更改成2。
注意,右下角的像素没有更改为2,
因为它不是在上下左右四个方向上与初始点相连的像素点。
注意:
image和image[0]的长度在范围[1, 50]内。- 给出的初始点将满足
0 <= sr < image.length和0 <= sc < image[0].length。 image[i][j]和newColor表示的颜色值在范围[0, 65535]内。
题目分析
首先理解这个用例输入输出:
对于输入的二维数组:
| 1 | 1 | 1 |
|---|---|---|
| 1 | 1 | 0 |
| 1 | 0 | 1 |
其中开始位置为 (1,1) 新的颜色为 2
所以整张图的遍历就从表中的 1 开始,并且需要从这个点上下左右进行遍历,如果满足特定条件,就进行 “渲染”:遍历到的点与初始点的颜色相同,即代表颜色的值相同。
输出结果为:
| 2 | 2 | 2 |
|---|---|---|
| 2 | 2 | 0 |
| 2 | 0 | 1 |
例2 为了确保自己已经理解了题目意思,不妨修改输入然后提交查看输出。
| 1 | 5 | 1 |
|---|---|---|
| 1 | 1 | 0 |
| 3 | 0 | 1 |
其中开始位置为 (1,1) 新的颜色为 2
输出结果为:
| 2 | 5 | 1 |
|---|---|---|
| 2 | 2 | 0 |
| 3 | 0 | 1 |
因为 3 和 5 不满足 渲染 条件,而 右边的两个 1 又因为隔离不能被 渲染.
在理解题意以后就方便写代码了,广度优先遍历与深度优先遍历都能解决问题,并且难易程度近似。这里直接摘录 官方解答 ,注意是考虑到代码简洁规范。
解题代码1——广度优先遍历(BFS)
class Solution
public:
// 成对出现,表示上下左右方向
const int dx[4] = 1, 0, 0, -1;
const int dy[4] = 0, 1, -1, 0;
vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int newColor)
// 当前的颜色;
int currColor = image[sr][sc];
// 如果已染色
if (currColor == newColor) return image;
int n = image.size(), m = image[0].size();
// 注意队列的数据类型是 pair
queue<pair<int, int>> que;
que.emplace(sr, sc);
image[sr][sc] = newColor;
while (!que.empty())
int x = que.front().first, y = que.front().second;
que.pop();
// 四个方向遍历
for (int i = 0; i < 4; i++)
int mx = x + dx[i], my = y + dy[i];
// 边界判定
if (mx >= 0 && mx < n && my >= 0 && my < m
&& image[mx][my] == currColor)
que.emplace(mx, my);
image[mx][my] = newColor;
return image;
;
复杂度分析
- 时间复杂度: O ( n × m ) O(n\\times m) O(n×m) ,其中 n n n 和 m m m 分别是二维数组的行数和列数。最坏情况下需要遍历所有的方格一次。
- 空间复杂度: O ( n × m ) O(n\\times m) O(n×m) ,其中 n n n 和 m m m 分别是二维数组的行数和列数。主要为队列的开销。
解题代码2——深度优先遍历(DFS)
DFS 用到了递归,但是总体思路也比较简单,一定要重点关注递归的终止条件。
class Solution
public:
const int dx[4] = 1, 0, 0, -1;
const int dy[4] = 0, 1, -1, 0;
void dfs(vector<vector<int>>& image, int x, int y, int color, int newColor)
// 如果颜色等于初始颜色就可以渲染
// 并且四个方向进行检测,渲染
if (image[x][y] == color)
image[x][y] = newColor;
for (int i = 0; i < 4; i++)
int mx = x + dx[i], my = y + dy[i];
// 边界判断
if (mx >= 0 && mx < image.size() && my >= 0 && my < image[0].size())
dfs(image, mx, my, color, newColor);
vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int newColor)
int currColor = image[sr][sc];
if (currColor != newColor)
dfs(image, sr, sc, currColor, newColor);
return image;
;
复杂度分析
- 时间复杂度: O ( n × m ) O(n\\times m) O(n×m) ,其中 n n n 和 m m m 分别是二维数组的行数和列数。最坏情况下需要遍历所有的方格一次。
- 空间复杂度: O ( n × m ) O(n\\times m) O(n×m) ,其中 n n n 和 m m m 分别是二维数组的行数和列数。主要为队列的开销。
复习一下 BFS 和 DFS
以下内容摘录自《数据结构(C 语言版)》电子档
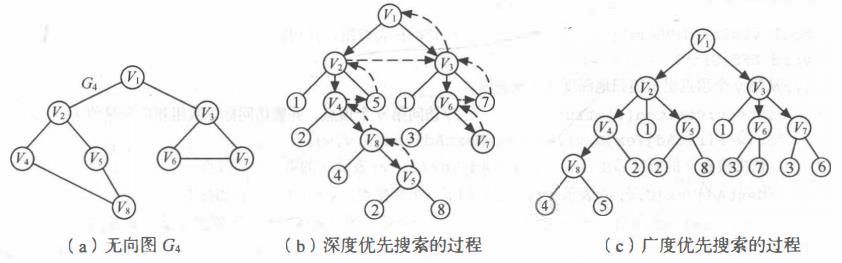
BFS
广度优先搜索(Breadth First Search, BFS)遍历类似于树的 按层次遍历 的过程。
广度优先搜索遍历的过程如下。
(1) 从图中某个顶点 v v v 出发,访问 v v v。
(2) 依次访问 v v v 的各个未曾访问过的邻接点。
(3) 分别从这些邻接点出发依次访问它们的邻接点, 并使 “先被访问的顶点的邻接点“ 先于 ”后被访问的顶点的邻接点” 被访问。重复步骤(3), 直至图中所有已被访问的顶点的邻接点都被访间到。
DFS
DFS (DepthFirst Search) 遍历类似于树的 先序遍历,是树的先序遍历的推广。
对于一个连通图,深度优先搜索遍历的过程如下。
(1) 从图中某个顶点 v v v 出发, 访问 v v v 。
(2) 找出刚访问过的顶点的第一个未被访问的邻接点, 访问该顶点。 以该顶点为新顶点,重复此步骤, 直至刚访问过的顶点没有未被访问的邻接点为止。
(3) 返回前一个访问过的且仍有未被访问的邻接点的顶点,找出该顶点的下一个未被访问的邻接点, 访问该顶点。
(4) 重复步骤 (2) 和 (3), 直至图中所有顶点都被访问过,搜索结束。
总结
刷这道题的主要目标是通过简单的题回顾一下 DFS 和 BFS 的基本思想以及如何结合实际应用(比如说遍历的时候的条件等)。相对于前面两道题这个应该更简单,更方便以最快的速度回顾一下以前的知识。
Smileyan
2021.8.15 23:16
以上是关于图论刷题-3力扣 733. 图像渲染的主要内容,如果未能解决你的问题,请参考以下文章