图论刷题-2剑指 Offer 12. 矩阵中的路径

Posted 2021-09-05 smile-yan

剑指 Offer 12. 矩阵中的路径

力扣题目地址 | 同题地址

难度与标签

中等难度

• 图
• 递归
• 回溯
• 深度优先搜索
• 广度优先搜索

题目描述

给定一个 m x n 二维字符网格 board和一个字符串单词 word 。如果 word存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例1：

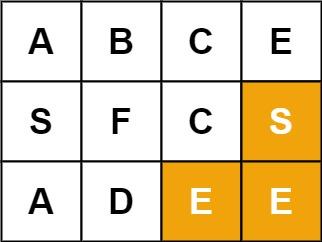
• 输入：board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCCED”
• 输出：true

示例2：

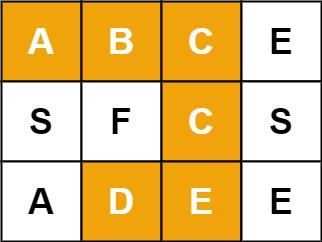
• 输入：board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “SEE”
• 输出：true

示例3：

• 输入：board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCB”
• 输出：false

提示：

• m == board.length

  n = board[i].length

• 1 <= m, n <= 6

• 1 <= word.length <= 15

• board 和 word 仅由大小写英文字母组成

进阶： 你可以使用搜索剪枝的技术来优化解决方案，使其在 board 更大的情况下可以更快解决问题？

问题分析与解答1

以下内容均参考[ 官方题解 ]

总体思路：从点 $P_0$​ 出发，确保 $P_0$ 等于字符串第一个字符 $s_0$，然后尝试各个方向前进，下一个点 $P_1$​ 等于 $s_1$ 则继续前进，否则继续确定 $P_0$。

class Solution {
public:
    /**
     * 这个函数是用来检查从 board[i][j] 开始匹配第 k 个字符
     以后的字符串否成功
     * board 输入的二维数组
     * visited 用来标记已经使用过的位置
     * i,j 当前的开始位置
     * s 目标字符串
     * k 字符串的位置
     */
    bool check(vector<vector<char>>& board, vector<vector<int>>& visited, 
               int i, int j, string& s, int k) {
        // 如果与预期值不匹配，直接就false
        if (board[i][j] != s[k]) {
            return false;
        } else if (k == s.length() - 1) {
            // 如果匹配并且已经是最后一个了，不用继续匹配了
            return true;
        }
        // 接下来的情况是：当前字符匹配并且还需要继续匹配后面的字符
        // 这个位置标记一下已经用过了
        visited[i][j] = true;
        // 方向
        vector<pair<int, int>> directions{{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
        
        bool result = false;
        // 遍历各个方向
        for (const auto& dir: directions) {
            // 新方向前进一个位置对应的坐标
            int newi = i + dir.first, newj = j + dir.second;
            // 剪枝；边界判断
            if (newi >= 0 && newi < board.size() && newj >= 0 
                    && newj < board[0].size()) {
                // 并且没有用过
                // 剪枝
                if (!visited[newi][newj]) {
                    // 递归
                    bool flag = check(board, visited, newi, newj, s, k + 1);
                    // 如果整个递归过程一直匹配
                    if (flag) {
                        result = true;
                        break;
                    }
                }
            }
        }
        // 用完了不管结果如何都设置没用过
        // 对下一次循环提供 无污染 环境
        visited[i][j] = false;
        return result;
    }

    bool exist(vector<vector<char>>& board, string word) {
        int h = board.size(), w = board[0].size();
        vector<vector<int>> visited(h, vector<int>(w));
        // 从每个点开始试探
        for (int i = 0; i < h; i++) {
            for (int j = 0; j < w; j++) {
                bool flag = check(board, visited, 
                                  i, j, word, 0);
                if (flag) {
                    return true;
                }
            }
        }
        return false;
    }
};

复杂度分析

• 时间复杂度：一个非常宽松的上界为 $O(MN\cdot 3^L)$ ，其中 $M$, $N$ 为网格的长度与宽度，$L$ 为字符串 $\text{word}$​ 的长度。在每次调用函数 $\text{check}$ 时，除了第一次可以进入 4 个分支以外，其余时间我们最多会进入 3 个分支（因为每个位置只能使用一次，所以走过来的分支没法走回去）。由于单词长为 $L$，故 $\text{check}(i,j,0)$ 的时间复杂度为 $O(3^L)$，而我们要执行 $O(MN)$ 次检查。然而，由于剪枝的存在，我们在遇到不匹配或已访问的字符时会提前退出，终止递归流程。因此，实际的时间复杂度会远远小于 $\Theta (MN\cdot 3^L)$。

• 空间复杂度：$O(MN)$ 。我们额外开辟了 $O(MN)$ 的 $\text{visited}$ 数组，同时栈的深度最大为 $O(\min (L,MN))$ 。

解答2

自己再次刷题的时候写的内容如下：

class Solution {
public:
    bool travel(int x, int y, int index, vector<vector<bool>>& visited,
                vector<vector<char>>& board, string word) {
        if (x < 0 || y < 0 || x >= board.size() || y >= board[0].size()) {
            return false;
        }
        if (visited[x][y]) {
            return false;
        }
        if (board[x][y] != word[index]) {
            return false;
        }
        if (index == word.length()-1) {
            return true;
        }
        
        visited[x][y] = true;

        // 如果成立其中一个就不继续了
        bool flag = false;
        if (travel(x+1, y, index+1, visited, board, word)) {
             return true;
        }
        if (travel(x-1, y, index+1, visited, board, word)) {
            return true;
        }
        if (travel(x, y+1, index+1, visited, board, word)) {
            return true;
        }
        if (travel(x, y-1, index+1, visited, board, word)) {
            return true;
        }
        
        visited[x][y] = false;
       
        return false;
    }
    bool exist(vector<vector<char>>& board, string word) {
        vector<vector<bool>> visited(board.size(), vector<bool>(board[0].size()));
        for (int i=0; i<board.size(); i++) {
            for (int j=0; j<board[0].size(); j++) {
                bool result = travel(i,j,0,visited,board,word);
                if (result) {
                    return true;
                }
            }
        }
        return false;
    }
};

方法跟方法1基本式一样的，只是我把剪枝条件也写在递归中了。

总结

题目中用到的数据结构包括：

• 向量 vector
• pair

整个题目思路是比较简单的，但是个人认为写代码具有一定的难度，主要需要考虑剪枝条件，如何递归寻找下一个匹配的字符，并且还需要考虑不管递归最终有没有找到目标字符串，都需要擦去用过的痕迹（回溯），防止影响下一次迭代递归。

Smileyan

2021.8.13 10:22