2021高教社杯E题

Posted 2022-01-18 zhuo木鸟

参考文献

1. Kmeans 聚类：https://towardsdatascience.com/k-means-clustering-algorithm-applications-evaluation-methods-and-drawbacks-aa03e644b48a
2. 三次插值法 Python：https://docs.scipy.org/doc/scipy/reference/reference/generated/scipy.interpolate.interp1d.html#scipy.interpolate.interp1d
3. 数值积分 Python：https://docs.scipy.org/doc/scipy-1.4.1/reference/generated/scipy.integrate.trapz.html
4. PCA 解释方差占比：https://ro-che.info/articles/2017-12-11-pca-explained-variance

本人专挑数据挖掘、机器学习和 NLP 类型的题目做，有兴趣也可以逛逛我的数据挖掘竞赛专栏。

如果本篇博文对您有所帮助，请不要吝啬您的点赞 😊

赛题官网：http://www.mcm.edu.cn/html_cn/node/4d73a36cc88b35bd4883c276afe39d89.html

文章目录

• 第一题
• • Kmeans 聚类
  • 距离表示
  • • 数据分析
    • 积分法表示距离
  • Kmeans 聚类法对曲线进行聚类
  • • Elbow 法选择聚类簇数
    • 第一问求解
  • 缺点与改进
  • • 该算法的缺点分析
    • 改进方法
• 第二题（第三题、第四题）
• • 聚类分析
  • 数据降维
  • 机器学习方法解决分类
  • • 筛选模型参数
    • • F1 值（补充介绍）
      • 多分类问题的评价指标介绍
    • 筛选最佳模型
  • 深度学习：多层感知器模型解决
  • • 特征预处理
    • 模型训练与结果
  • 第三题、第四题
• 代码与提问

第一题

第1题旨在根据附件一给出的不同编号的药材的中红外谱数据，研究药材的种类。意思已经很明显了，就是一个聚类的问题。

传统的聚类算法在这个问题中是不适用的原因在于：在中红外谱数据中，每个药材的数据（每一行），以其说可以看成一个点，不如说可以看成一条线，这是一个线的聚类问题，而非点的聚类问题。

因此如果用碘的聚类去解决，就会导致“点”的维度太多，而数据量较少，导致聚类的效果不好。另一方面，附件一中的数据已经帮我们标准化过了，并且每一列的数据的量纲都是相同的，因此我们不能直接套用点的聚类去解决这个问题。

当然我们可以结合点的聚类来进行线的聚类，为了更好的阐述，我们首先简要地介绍一下，点聚类的常见方法： Kmeans 聚类方法

Kmeans 聚类

这里采用的 Kmeans 聚类算法如下：

$$\begin{array}{rl}\text{1、}& \text{选择一个聚类簇数 K}\\ \text{2、}& \text{从数据集中任意地选出个 K 个点，作为聚类中心}\\ \text{ 3、}& \text{求出数据集中的每个点与这 K 个聚类簇的距离，并根据与聚类簇距离的远近，将数据划分成 K 个子数据集}\\ \text{ 4、}& \text{将 K 个子数据集的均值作为新的聚类中心}\\ \text{ 5、}& \text{重复步骤 3、4，直到聚类簇不发生变化为止}\end{array}$$

距离表示

若采用上述的聚类算法，我们可以看到最关键的一步是如何表示数据集中的每个点与聚类簇的距离：

数据分析

为了更好的分析数据，我们首先将数据进行可视化。当然将所有附件一中的药材的红外谱图画出来是有点不现实的，因此我们挑出编号为0 100 200 300 400的5个药材来展示，其药材的中红外谱图如下所示：

从上图可以看出药材 200 很明显与其他药材的差距是很大，这是因为药材 200 的吸光度曲线，与其他药材的吸光度曲线的 "距离” 太大了。

积分法表示距离

对于直线来说距离比较好求，但对于曲线来说，距离应该如何定量表示呢？

这里可以考虑采用积分的方法：
$$\begin{array}{r}\text{距离}={\int }_{x=652}^{3999}|y_1-y_2|dx\end{array}$$
式中， $y_1,y_2$ 分别为用于求距离的两种药材的曲线，采用上述公式就可以将曲线与曲线之间的距离量化表示。

鱿鱼我们没有曲线的具体表达式，因此只能用数值积分来求解，但是鉴于 X 轴的数据点间隔比较大，进行积分时产生的误差就会较大。因此在进行积分之前，我们可以采用三次插值法，进行数据填充，从而提高积分的精度。

Kmeans 聚类法对曲线进行聚类

如上所述，我们可以采用 Kmeans 聚类法对曲线进行聚类，同时用上述的积分法求解的距离，作为划分子数据集，从而产生不同的聚类簇，聚类中心由子数据集的所有数据的均值产生。

很多时候，采用 Kmeans 进行聚类，会因为聚类中心的初始化，导致在划分子数据及时，有些聚类中心会没有用到。例如选定的聚类簇数 K，很有可能因为聚类中心的初始化不当，导致仅划分出了 K-1 各个子数据集。另外选择一个较好的初始化聚类中心，也可以提高算法的迭代效率，这里采用的一种初始化聚类中心的方法如下所示：
$$\begin{array}{rl}\text{1、}& \text{选择一个聚类簇数 K}\\ \text{2、}& \text{从数据集}X\in x_1,x_2,\cdots ,x_n\text{中任意地选出个 1 个点，作为第一个聚类中心，记为}{c}_1\\ \text{3、}& \text{根据概率}\frac{D(x_i{)}^2}{{\sum }_{i=1}^{n}D(x_i{)}^2}\text{从}X\text{中选出}{c}_2,D(x_i)\text{为}{x}_i\text{与}c\text{的距离}\\ \text{4、}& \text{重复步骤 3 直到聚类中心数为 K}\end{array}$$
在产生新的聚类中心时，距离公式 $D(x_i)$ 应是 $x_i$ 与目前为止被选中的所有聚类中心 $c=c_1,c_2,\cdots$ 的距离之和。

Elbow 法选择聚类簇数

采用 Kmeans 方法进行聚类11个比较困难的点在于聚类簇数的选择上，虽然聚类簇数的选择具有一定的主观性，但是我们可以借助一些方法，来帮助我们选择一个较好地聚类簇数 K。

这里我们遍历 $K=1,2,\cdots ,21$，并求出每一个 K 下，数据集与其各自的聚类中心的距离之和，如下图所示：

根据 Elbow 图的拐点原则，可以选择 K=4,8,12,16 作为聚类簇数。考虑到距离之和越小聚类的效果越好，因此这里选择 K=8 作为最终的聚类簇数。

第一问求解

综上所述，我们选择 K=8 的 Kmeans 聚类法，对附录 1 中的数据进行聚类，最终得出 8 个聚类中心如下所示：

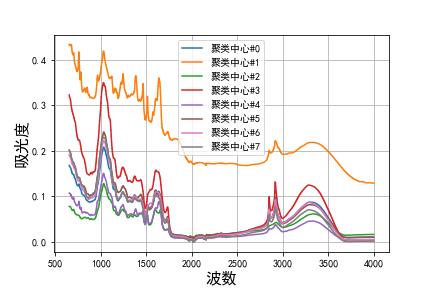
实际上从上图也可以看出，将聚类簇数设置为 K=2 会好一点，我们在求解 K=2 的情况，得出各聚类中心的中红外谱图如下所示：

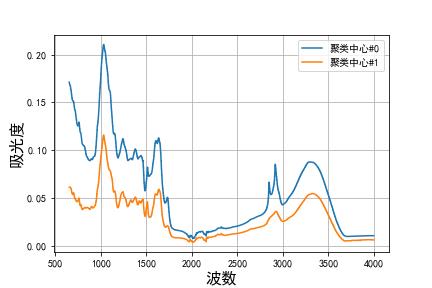
K=8 时，在我们的结果中，子数据集 k=0 也就是聚类簇 0 的数量占了绝大部分，其他聚类簇包含的数据量仅仅为 1~2 个！所以可以认为，附件一中包含的药材种类大致有8种档，其中有一种占了绝大部分，其红外光谱图的特性，如上图的蓝色曲线所示（K=8时），这里就不再多做赘述了。

缺点与改进

该算法的缺点分析

上述聚类得出某一聚类簇包含的数据量及占绝大多数，这实际上可能意味着聚类的效果并不好！笔者亦调整了距离的计算公式，如用：
$${\int }_{x=652}^{3999}(y_1-y_2{)}^{2}dx$$
Down得出的聚类的效果都差不多，依旧是某个聚类簇包含的数据量占绝大多数。这可能是以下三个原因造成的：

1. 聚类簇数的选择不够恰当，应该再选多一点；
2. 数据集原本就是这样；
3. 以积分表示距离，实际上忽略了曲线的细节。比如一条曲线的前半部分和另一条曲线的后半部分，与聚类中心对应的部分的差距是相同的，那么这两条曲线可能会被归为一类！（这可能是主要原因）

改进方法

如果真的要改进，应该破而后立，不能再用这种以积分的形式表示距离，从而采用点聚类的方法来聚类曲线。我们可以考虑传统的点聚类方法，然后将每一段波数的数据采用均值等方式合并成一列，从而降低数据量，在采用点距类的方式进行聚类即可。

虽然这样做也会造成一些细节无法体现，但考虑到同一个药材的情况下，波数 $x$ 附近的波数区间 $[x-\delta ,x+\delta ]$ 的吸光率是非常接近的，因此这些细节忽略了也影响不大，所以可以这么做。

博主这里没有实现这种改进方法，各位聪明的读者可以根据我的代码，自己实现一个。

第二题（第三题、第四题）

说实话，这一题我想了很久，因为像这种比赛的话，一般是第1题要作为第2题的基础的。但我们第一题，采用了曲线聚类的方法，难以分析出各波段的特征。理想的第1题的解法应该是考虑并分析各波段的数学特性，再来进行聚类；或者将数据进行降维，再来进行聚类。于是第2题可以在第1题的基础上进行数据降维，于是问题二并可以作为一个机器学习的经典问题——分类问题来解决。

所以我们在第2题中考虑，先考虑将数据进行降维。在此之前，我们先用上述曲线锯类的方法，对附件2的数据进行一番分析吧。

聚类分析

选择聚类簇数为 K=9，对附件2的数据进行聚类，得到9个聚类中心，如下图所示：

根据聚类结果来看，依旧是聚类簇 0 占了绝大部分数据。从上图来看，聚类中心 0 比较棱角鲜明，因此我们也可以猜到大部分的药材都是差不多跟聚类中心 0 一样的曲线走向的。

另外从上图也可以看出，聚类的几个聚类中心，它们都比较接近，换句话说，这个药材可能是同一种药材，只是因为他们的场地不同导致他们的吸光率不同罢了。

从上图可以看出我们完全可以将数据，作为用于分类问题的机器学习训练数据和测试数据。

数据降维

我们对数据进行 PCA 降维，为了观察 PCA 降维后的效果，我们可以采用解释方差占比来衡量。所谓解释方差占比可以定量地衡量，数据在降维前后其相似度，或者信息量的保留程度，当解释方差占比为 1 时，可以证明降维前后数据是等效的。

数据再进行 PCA 降维后，若原始数据（高维度）能够以较少的正交数据（低纬度）完全表示，则数据转换前后原始数据的总方差，欲穷转换后的数据的总方差是相等的。

PCA 降维原理是在于：

设原始数据 $X=(x_1,x_2,\cdots ,x_n)$，转换后的数据为 $X^{\prime }=(x_1^{\prime },x_2^{\prime },\cdots ,x_n^{\prime })$，变量 $2021高教社杯E题$

2021数学建模国赛 || 高教社杯 || 赛题 || 思路

2022年高教社杯全国大学生数学建模竞赛-赛题解析篇E题：小批量物料的生产安排

2021高教社杯-国赛ABCD题-解题思路-数学建模

2021高教社杯-国赛ABCD题-解题思路-数学建模

2022年高教社杯国赛E题思路——小批量物料的生产安排