LeetCode 1610. 可见点的最大数目（计算角度） / 1518. 换酒问题 / 419. 甲板上的战舰

Posted 2022-01-13 Zephyr丶J

1610. 可见点的最大数目

2021.12.16 每日一题

题目描述

给你一个点数组 points 和一个表示角度的整数 angle ，你的位置是 location ，其中 location = [posx, posy] 且 points[i] = [xi, yi] 都表示 X-Y 平面上的整数坐标。

最开始，你面向东方进行观测。你 不能 进行移动改变位置，但可以通过 自转 调整观测角度。换句话说，posx 和 posy 不能改变。你的视野范围的角度用 angle 表示， 这决定了你观测任意方向时可以多宽。设 d 为你逆时针自转旋转的度数，那么你的视野就是角度范围 [d - angle/2, d + angle/2] 所指示的那片区域。
对于每个点，如果由该点、你的位置以及从你的位置直接向东的方向形成的角度 位于你的视野中 ，那么你就可以看到它。

同一个坐标上可以有多个点。你所在的位置也可能存在一些点，但不管你的怎么旋转，总是可以看到这些点。同时，点不会阻碍你看到其他点。

返回你能看到的点的最大数目。

示例 1：

输入：points = [[2,1],[2,2],[3,3]], angle = 90, location = [1,1]
输出：3
解释：阴影区域代表你的视野。在你的视野中，所有的点都清晰可见，尽管 [2,2] 和 [3,3]在同一条直线上，你仍然可以看到 [3,3] 。

示例 2：

输入：points = [[2,1],[2,2],[3,4],[1,1]], angle = 90, location = [1,1]
输出：4
解释：在你的视野中，所有的点都清晰可见，包括你所在位置的那个点。

示例 3：

输入：points = [[1,0],[2,1]], angle = 13, location = [1,1]
输出：1
解释：如图所示，你只能看到两点之一。

提示：

1 <= points.length <= 10^5
points[i].length == 2
location.length == 2
0 <= angle < 360
0 <= posx, posy, xi, yi <= 100

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximum-number-of-visible-points
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目描述

思路其实很简单，就是计算每个点与观测点形成的角度大小，然后用滑动窗口的方法，看所给角度范围内最多能看到多少个点
主要问题就是怎么计算角度
还有需要注意，需要将角度范围扩充到720，否则会漏掉情况；和观测点重合的点，需要单独考虑

计算角度的API：
static double atan​(double a)
Returns the arc tangent of a value; the returned angle is in the range -pi/2 through pi/2.

static double atan2​(double y, double x)
Returns the angle theta from the conversion of rectangular coordinates (x, y) to polar coordinates (r, theta).

相比较ATan，ATan2究竟有什么不同？

对于tan(θ) = y / x:

θ = ATan(y / x)求出的θ取值范围是[-PI/2, PI/2]。

θ = ATan2(y, x)求出的θ取值范围是[-PI, PI]。

当 (x, y) 在第一象限, 0 < θ < PI/2.
当 (x, y) 在第二象限 PI/2 < θ≤PI.
当 (x, y) 在第三象限, -PI < θ < -PI/2.
当 (x, y) 在第四象限, -PI/2 < θ < 0.

当点(x, y)在象限的边界也就是坐标轴上时:

当 y 是 0，x 为非负值, θ = 0.
当 y 是 0， x 是 负值, θ = PI.
当 y 是 正值， x 是 0, θ = PI/2.
当 y 是 负值， x 是 0, θ = -PI/2.

class Solution 
    public int visiblePoints(List<List<Integer>> points, int angle, List<Integer> location) 
        //思路其实还是挺简单的，就是将每个点与中心点相连，然后计算出每个点的角度
        //然后用滑动窗口得到angle里面能观测到多少点

        //首先要知道计算角度的函数，Math.atan2，算出来的是一个极坐标，也就是范围是-π，π
        
        List<Double> list = new ArrayList<>();
        int samep = 0;  //与中心点相同的点
        for(List<Integer> temp : points)
            if(temp.get(1) == location.get(1) && temp.get(0) == location.get(0))
                samep++;
                continue;
            
            double p = Math.atan2(temp.get(1) - location.get(1), temp.get(0) - location.get(0));
            list.add(p);
        
        //先排序
        Collections.sort(list);
        int n = list.size();
        double pi = Math.PI;
        double _angle = angle * pi / 180;
        //System.out.println(_angle);
        //因为如果视线在第一和第四象限，滑动窗口就没法遍历到，所以需要扩展这个list
        for(int i = 0; i < n; i++)
            list.add(list.get(i) + 2 * pi);
        
        //System.out.println(list);
        //滑动窗口得到结果
        int max = 0;
        int left = 0;
        int right = 0;
        
        while(right < 2 * n)
            while(left < right && list.get(right) - list.get(left) > _angle)
                left++;
            max = Math.max(max, right - left + 1);
            right++;
        
        
        return max + samep;

    

1518. 换酒问题

2021.12.17 每日一题

题目描述

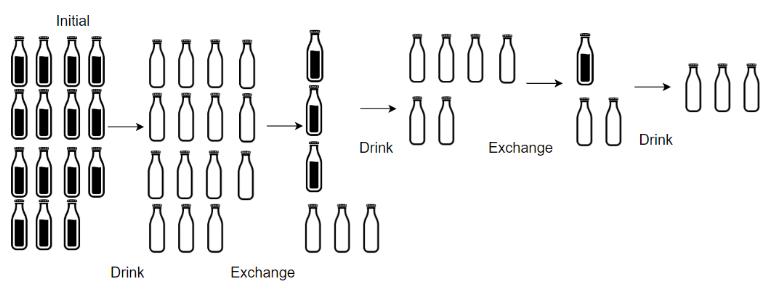
小区便利店正在促销，用 numExchange 个空酒瓶可以兑换一瓶新酒。你购入了 numBottles 瓶酒。

如果喝掉了酒瓶中的酒，那么酒瓶就会变成空的。

请你计算 最多 能喝到多少瓶酒。

示例 1：

输入：numBottles = 9, numExchange = 3
输出：13
解释：你可以用 3 个空酒瓶兑换 1 瓶酒。
所以最多能喝到 9 + 3 + 1 = 13 瓶酒。

示例 2：

输入：numBottles = 15, numExchange = 4
输出：19
解释：你可以用 4 个空酒瓶兑换 1 瓶酒。
所以最多能喝到 15 + 3 + 1 = 19 瓶酒。

示例 3：

输入：numBottles = 5, numExchange = 5
输出：6

示例 4：

输入：numBottles = 2, numExchange = 3
输出：2

提示：

1 <= numBottles <= 100
2 <= numExchange <= 100

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/water-bottles
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

生活中很常见的一个问题

class Solution 
    public int numWaterBottles(int numBottles, int numExchange) 
        int emp = numBottles; //当前空瓶子的数目
        int res = numBottles;
        //如果空瓶子的个数大于交换的个数，说明还能喝
        while(emp >= numExchange)
            //当前能换的酒的个数
            int temp = emp / numExchange;
            emp = emp % numExchange;
            emp += temp;
            res += temp;
        
        return res;

    

numExchange能换一瓶酒，所以相当于用了numExchange - 1 个空瓶子
而每次需要保留一个瓶子来装酒，所以不能都换了

class Solution 
    public int numWaterBottles(int numBottles, int numExchange) 
        return numBottles + (numBottles - 1) / (numExchange - 1);
    

419. 甲板上的战舰

2021.12.18 每日一题

题目描述

给你一个大小为 m x n 的矩阵 board 表示甲板，其中，每个单元格可以是一艘战舰 ‘X’ 或者是一个空位 ‘.’ ，返回在甲板 board 上放置的 战舰 的数量。

战舰 只能水平或者垂直放置在 board 上。换句话说，战舰只能按 1 x k（1 行，k 列）或 k x 1（k 行，1 列）的形状建造，其中 k 可以是任意大小。两艘战舰之间至少有一个水平或垂直的空位分隔 （即没有相邻的战舰）。

示例 1：

输入：board = [[“X”,".",".",“X”],[".",".",".",“X”],[".",".",".",“X”]]
输出：2

示例 2：

输入：board = [["."]]
输出：0

提示：

m == board.length
n == board[i].length
1 <= m, n <= 200
board[i][j] 是 ‘.’ 或 ‘X’

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/battleships-in-a-board
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

其实感觉没有进阶那句话，一般也不会想到直接这样遍历
两个战舰不能相邻很关键

class Solution 
    public int countBattleships(char[][] board) 
        //一次扫描，还是O(1)的算法，还不能修改表格的值
        //当时想的是因为两艘战舰之间有空格分隔，所以横着遍历，找到一个X，
        //然后看上面是否有相邻的，如果有就不用增加战舰的数量，如果没有就增加

        int m = board.length;
        int n = board[0].length;

        int res = 0;
        //横向遍历
        for(int i = 0; i < m; i++)
            for(int j = 0; j < n; j++)
                //如果当前为X，看上面和左边是不是X，如果不是数量加1
                if(board[i][j] == 'X')
                    if(i > 0 && j > 0)
                        if(board[i - 1][j] != 'X' && board[i][j - 1] != 'X')
                            res++;   
                    
                    else if(j > 0)
                        if(board[i][j - 1] != 'X')
                            res++;
                    else if(i > 0)
                        if(board[i - 1][j] != 'X')
                            res++;
                    else
                        res++;
                    
                
            
        
        return res;