leetcode 1301. 最大得分的路径数目

Posted 2021-05-20 大忽悠爱忽悠

---

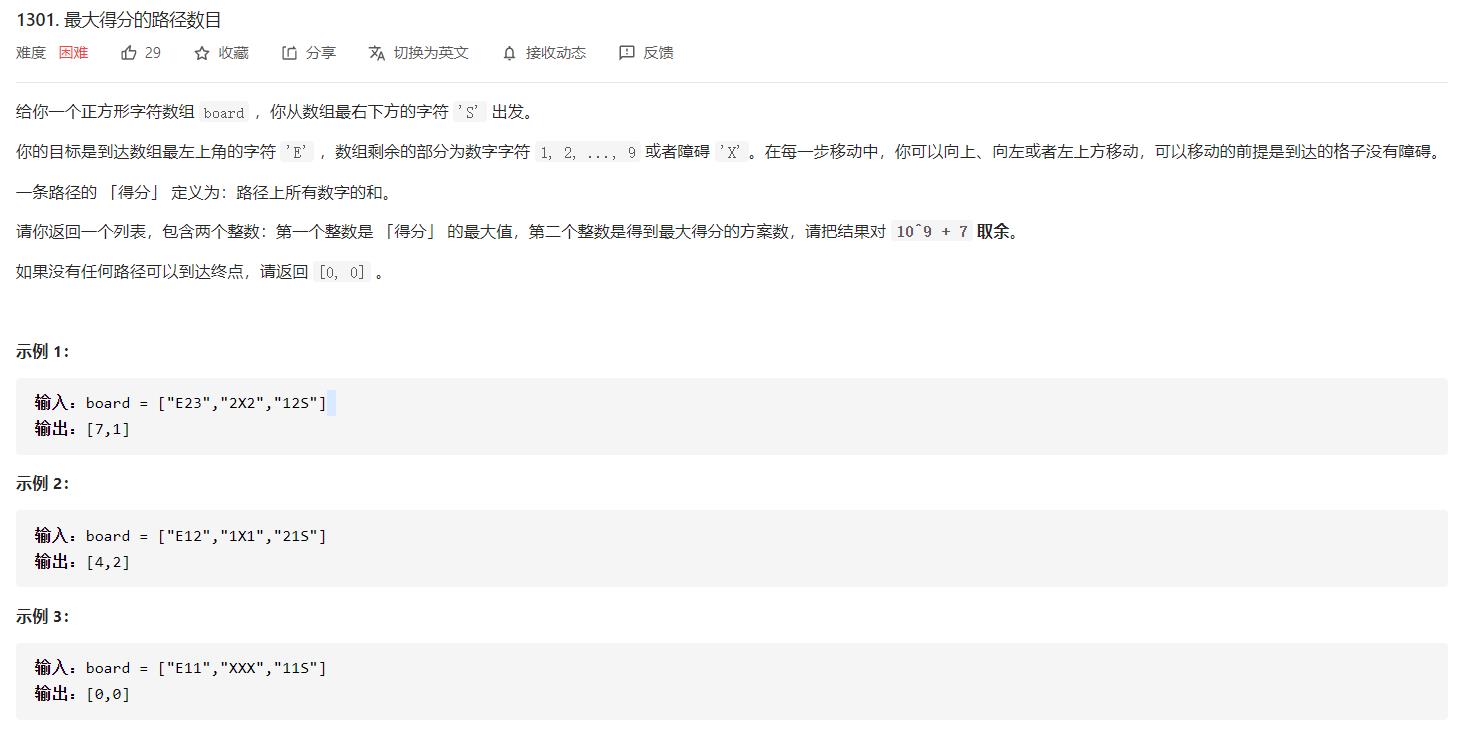
最大得分的路径数目题解集合

• 记忆化搜索--DFS
• 动态规划
• 总结

---

记忆化搜索–DFS

• 首先我们来看看递归的结束条件应该是什么:

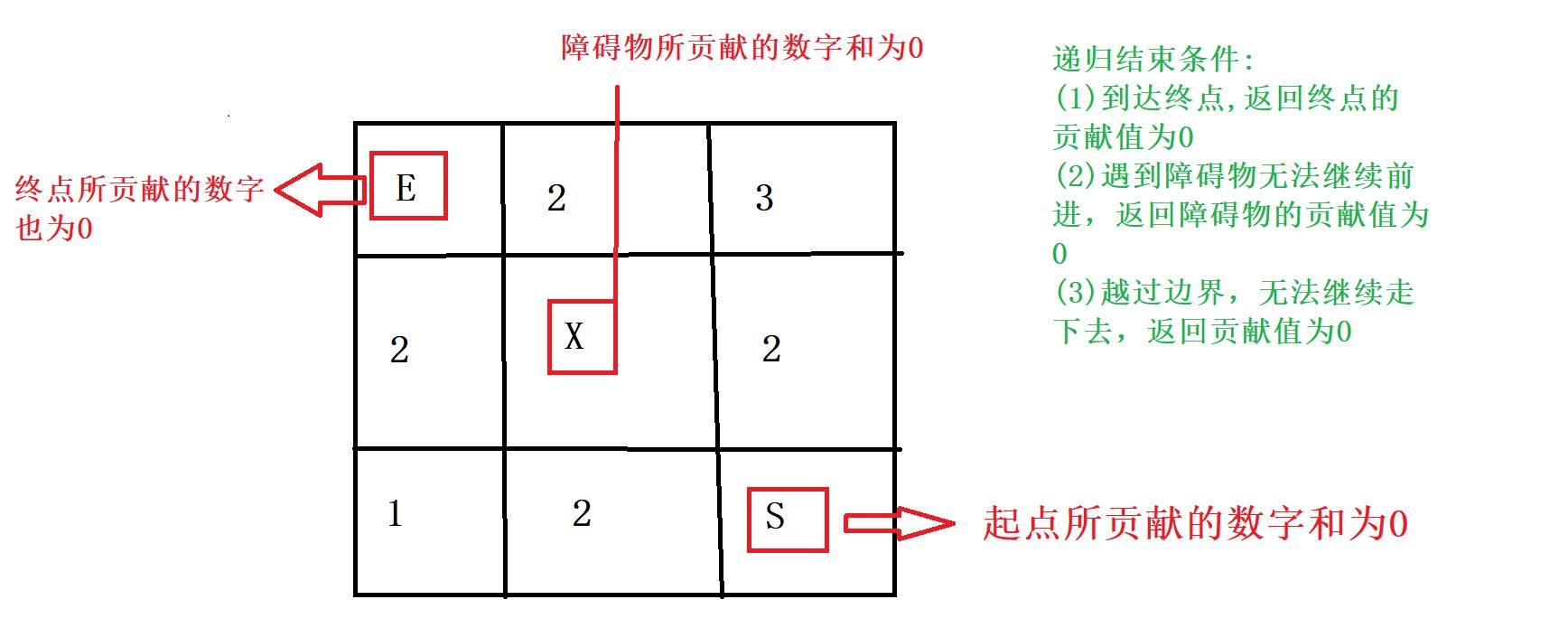
• 再来看看如何求解当前位置的最大贡献值:

注意：虽然这里是从右下角到达左上角，但实际上还是属于自下而上的递归，相当于求终点开始到达起点的最大贡献值，那么此时对于任意一个位置(i,j)来说，只有它的左边，左上和上方可以到达该位置

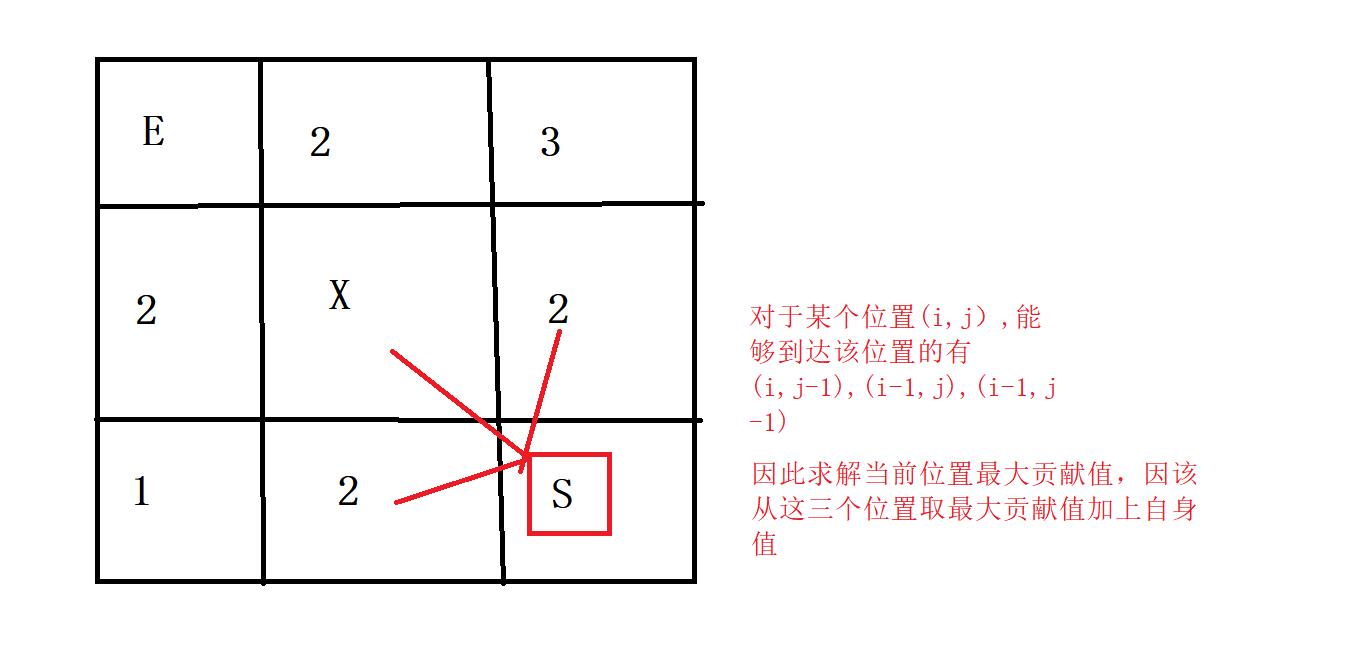
• 由此得出递归三部曲:
  1.递归结束条件:到达终点，遇到障碍物，越过边界
  2,本级递归做什么:求解当前位置最大贡献值
  3,返回值:返回当前位置最大贡献值

但是注意本题还要求求出最大贡献值的方案数，如何求解呢?
这里大家就直接看下面代码即可理解
代码:

class Solution {
	map<pair<int, int>, pair<int, int>> ret;//缓存器，用来保存当前位置最大贡献值和得到最大贡献值的方案数量
	int mod = 1e9 + 7;
public:
	vector<int> pathsWithMaxScore(vector<string>& board)
	{
		int r = board.size();
		int s= dfs(board, r - 1, r - 1).first;
		int n = dfs(board, r - 1, r - 1).second;
		return {s,n};
	}
	pair<int,int> dfs(vector<string>& board, int i, int j)
	{
		//当前位置的结果已经计算得出
		if (ret.find({ i,j }) != ret.end()) return ret[{i, j}];
		//越界
		if (i < 0 || j < 0 || i >= board.size() || j >= board.size())
			return { 0,0 };
		//如果当前位置到达终点，那么终点的最大贡献值为0，到达终点说明得到一个方案
		if (i==0&&j==0)
			return {0,1};
		//如果当前位置遇到障碍物，那么当前位置的最大贡献值为0，方案数为0，因为当前路径为无效路径
		if (board[i][j] == 'X')
			return {0,0};
		int s1 = dfs(board, i, j - 1).first;
		int s2 = dfs(board, i - 1, j).first;
		int s3 = dfs(board, i - 1, j - 1).first;
		int n1 = dfs(board, i, j - 1).second;
		int n2 = dfs(board, i - 1, j).second;
		int n3 = dfs(board, i - 1, j - 1).second;
		//先计算出三个方向中的最大贡献值
		int maxScore = getmax(s1, s2, s3);
		//计算出三个方向的最大方案数
		int maxNum = getmax(n1, n2, n3);
		//如果三个方向的最大方案数不为0,说明可以到达这个(i,j)坐标，我们就把最大的分数和当前格子的分数相加
		if (maxNum)
		{
			if (board[i][j] == 'S')
				ret[{i, j}].first = maxScore % mod;
			else
			ret[{i, j}].first = (maxScore + board[i][j] - '0') % mod;
		}
		else
			ret[{i, j}].first = 0;
		int num = 0;//方案数量
		//看看是否有不同的方式得到同样的最大贡献值
		if (maxScore == s1)
		{
			num = (n1 + num) % mod;
		}
		if (maxScore == s2)
		{
			num = (n2 + num) % mod;
		}
		if (maxScore == s3)
		{
			num = (n3 + num) % mod;
		}
		ret[{i, j}].second = num % mod;
		return ret[{i, j}];
	}
	int getmax(int a, int b, int c)
	{
		return max(a, max(b, c));
	}
};

---

动态规划

思路:
其实就是对上面记忆化搜索的翻译过程，这里不做详细解释，大家可以看下面的代码思考
但这里注意要对边界的值要提前求出来，作为最小子问题

注意:字符和整数相加得出整数的方法: 3 + board[0][1] - '0'

	vector<string> board =
	{
		"E23","2X2","12S"
	};
	cout << board[0][1] - '0' << endl;
	cout<<3 + board[0][1] - '0' << endl;
	cout << 3 + board[0][1] << endl;
	cout << 3 + '5' - '0' << endl;

代码:

class Solution {
/**
dp[i][j].first 为(i,j)位置的最大得分
dp[i][j].second 为(i,j)位置的最大得分方案数
我们可以从'E'出发到'S' 就是从一个格子能往右、下和右下三个方向走，即能从三个格子到达(i,j)坐标
**/
public:
	vector<int> pathsWithMaxScore(vector<string>& board) 
	{
		int mod = 1e9 + 7;
		int n = board.size();
		vector<vector<pair<int, int>>> dp(n, vector<pair<int, int>>(n, {0,0}));//都初始化为0 0
		//起点的最大得分为0，方案数为1
		dp[0][0].second = 1;
		//处理边界
		for (int i = 1; i < n; ++i)
		{
			//如果边界上没有出现障碍物，那么就可以一直走下去，一旦出现障碍物就无法继续走下去了
			if (board[i][0] != 'X' && board[i - 1][0] != 'X')
			{
				//第一列上每一个位置的路径和等于它前面一个的路径和加上自身
				dp[i][0].first += (board[i][0] - '0' + dp[i - 1][0].first) % mod;
				//方案数等于前面一个的方案数
				dp[i][0].second = dp[i - 1][0].second % mod;
			}
			if (board[0][i] != 'X' && board[0][i - 1] != 'X')
			{
				//第一行上每一个位置的路径和等于它前面一个的路径和加上自身
				dp[0][i].first += (board[0][i] - '0' + dp[0][i-1].first) % mod;
				//方案数等于前面一个的方案数
				dp[0][i].second = dp[0][i-1].second % mod;
			}
		}
		int curnum;//当前格子的分数
		int curmax;//可以从三个方向(格子)走到(i,j) 这个curmax就是三个方向(格子)当前最大的得分
		int curstep;//可以从三个方向(格子)走到(i,j) 这个curmax就是三个方向(格子)当前的方案数
		for (int i = 1; i < n; ++i)
		{
			for (int j = 1; j < n; ++j)
			{
				char cur = board[i][j];
				if (cur == 'X')//如果当前格子放置了障碍物，那么不管，障碍物处的路径和默认为0，方案数为0
					continue;
				if (cur== 'S')//如果当前格子为'S'的话分数为0
					curnum = 0;
				else
					curnum = board[i][j] - '0';//获得当前格子的分数
				curmax = getmax(dp[i - 1][j].first, dp[i][j - 1].first, dp[i - 1][j - 1].first);//获取三个方向的最大得分
				curstep = getmax(dp[i - 1][j].second, dp[i][j - 1].second, dp[i - 1][j - 1].second);//获取三个方向的最大方案数
				if (curstep)//如果三个方向的最大方案数不为0,说明可以到达这个(i,j)坐标，我们就把最大的分数和当前格子的分数相加
					dp[i][j].first = (curmax + curnum) % mod;
				//下面三个if是把最大分数为curmax的方向的方案数累加到(i,j)的方案数
				if (dp[i - 1][j].first == curmax)
					dp[i][j].second = (dp[i][j].second + dp[i - 1][j].second) % mod;
				if (dp[i][j - 1].first == curmax)
					dp[i][j].second = (dp[i][j].second + dp[i][j - 1].second) % mod;
				if (dp[i - 1][j - 1].first == curmax)
					dp[i][j].second = (dp[i][j].second + dp[i - 1][j - 1].second) % mod;

			}
		}
		return { dp[n - 1][n - 1].first,dp[n - 1][n - 1].second };//返回最后一个格子的分数和方案数
	}
	int getmax(int a, int b, int c) 
	{
		return max(a, max(b, c));
	}
};

---

总结

本题难度方面还是比较大的，我的功力尚浅可能无法解释透彻，如果不理解可以私信我