PCA主成分分析（降维）
Posted elkluh
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了PCA主成分分析（降维）相关的知识，希望对你有一定的参考价值。
主成分分析的作用是降维。当数据量有多个维度时，有些维度对于数据的贡献大，有些维度对数据的贡献小。通过主成分分析，找到重要的维度，能大大减少计算量。
PCA的中心思想：
一个中心：原始特征空间的重构。
两个基本点：最大投影方差，最小重构距离。
---------------------------------------------------------------------------------------------------------------------------------
最小重构距离通过下面的式子来构建。
重构前：(xn是去中心化的每个样本)
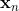表示原始的点，能表示成d个向量（d个维度）的和。通过分解，它能够分解到两组向量上，PCA保留了一部分，舍弃了一部分，舍弃了
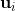这部分，保留了
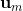这部分。a是每个分解的向量u上的长度，相乘后求和就可以重构原样本。
重构后：
重构的代价就是使重构前后的距离最小：（两个式子相减后剩下后面这部分）
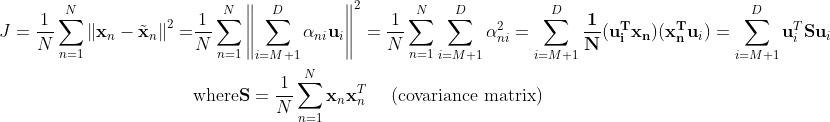
这里的S是协方差矩阵。
则损失函数为：
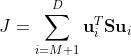
使用拉格朗日乘子约束优化，式子变成：
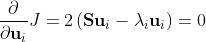
则：
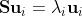
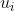表示S的特征向量，
表示特征值 。
---------------------------------------------------------------------------------------------------------------------------------
则PCA的步骤为：
1.求平均值，去中心化
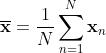
2.计算协方差矩阵
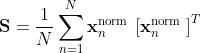
3.特征分解
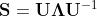
矩阵分解的过程就像下面这样子
4.用特征值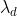
对U的列进行排序
5.选择M个特征向量，形成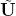
6.进行投影
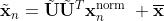
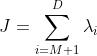
以上是关于PCA主成分分析（降维）的主要内容，如果未能解决你的问题，请参考以下文章