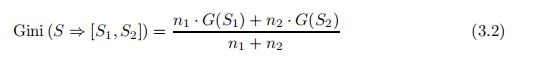推荐系统笔记：决策树&回归树

Posted 2022-01-10 UQI-LIUWJ

         决策树和回归树经常用于数据分类。 决策树是为那些因变量（target，label）是分类的情况而设计的，而回归树是为那些因变量（target，label）是数值的情况而设计的。

         在讨论决策树对协同过滤的泛化之前，我们将首先讨论决策树在分类中的应用。

1 决策树在分类/回归中的应用

        考虑我们有一个 m×n 矩阵 R 的情况。不失一般性，假设前 (n − 1) 列是自变量（x)，最后一列是因变量（y）。

         为了便于讨论，假设所有变量都是二进制的。 因此，我们将讨论创建决策树而不是回归树。 稍后，我们将讨论如何将这种方法推广到其他类型的变量。

         决策树是数据空间的分层划分，使用一组分层决策，称为自变量中的拆分标准。

        在单变量决策树中，一次使用单个特征来执行拆分。例如，在特征值为 0 或 1 的二元矩阵 R 中，特征变量值为 0 的所有数据记录将位于一个分支中，而所有数据取值为 1 的特征变量将位于另一个分支中。大多数属于不同类的记录将被分离出来。

        当决策树中的每个节点都有两个子节点时，生成的决策树称为二叉决策树。

1.1 Gini指数 

      衡量决策树分裂的质量可以通过使用分裂产生的子节点的加权平均基尼指数来评估。

         如果 p1 ...pr 是节点 S 中属于 r 个不同类的数据记录的占比，则该节点的基尼指数 G(S) 定义如下：

        

        ——>一个节点的Gini系数

         基尼指数介于 0 和 1 之间，数值越小，越表明判别力越大。

        比如我们有六个点

S的两个分支节点各有多少个节点	S的Gini系数
(6,0)	1-(1)**2-(0)**2=0
(4,2)	1-(1/3)**2-(2/3)**2=0.44
(3,3)	1-(1/2)**2-(1/2)**2=0.5

        可以看出，S点越不确定属于哪一类，Gini系数越大

        分裂的整体基尼指数等于子节点基尼指数的加权平均值。

        在这里，节点的权重由其中的数据点数定义。

         因此，如果 S1 和 S2 是二叉决策树中节点 S 的两个子节点，分别有 n1 和 n2 条数据记录，那么分裂 S ⇒ (S1, S2) 的基尼指数可以计算如下         

        

1.2 构造决策树

        Gini 指数用于选择适当的属性以用于在树的给定级别执行拆分。

        可以根据公式 3.2 测试每个属性以评估其拆分的基尼指数。选择基尼系数最小的属性进行拆分。

        该方法以自上而下的方式分层执行，直到每个节点仅包含属于特定类别的数据记录。或者，当节点中的最小部分记录属于特定类时，也可以提前停止树的生长。

        这样的节点被称为叶节点，它被标记为该节点中记录的主导类。

        当我们需要对一个示例进行分类时，我们就可以根据我们构造的决策树来为这个示例设定一条路径。叶子的标签将是该实例的标签。        

        

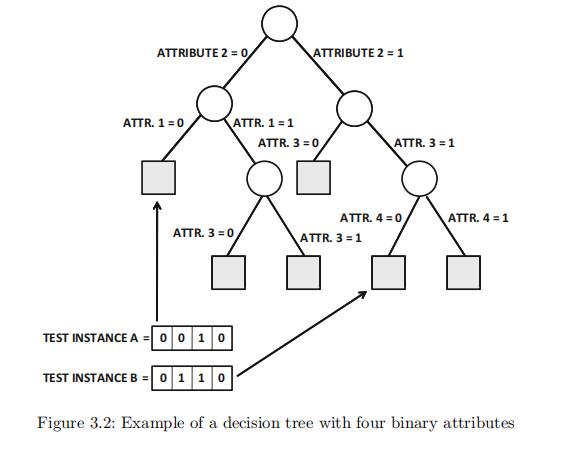
        图 3.2 说明了一个基于四个二元属性构建的决策树示例。树的叶子节点在图中用阴影表示。··        注意，决策树不一定使用所有属性进行拆分。例如，最左边的路径使用属性 1 和 2，但不使用属性 3 和 4。

        此外，决策树中的不同路径可能使用不同的属性序列。这种情况在高维数据中尤为常见。

        测试实例 A=0010 和 B=0110 到相应叶节点的映射示例如图 3.2 所示。由于数据分区的分层性质，这些测试实例中的每一个都被映射到唯一的叶节点。

1.3 多类别属性 & 连续数值属性 的决策树 

        该方法可以扩展到数值自变量，只需稍作修改。

        为了处理数值特征变量，可以将属性值划分为多个区间以执行拆分，其中拆分的每个分支对应于不同的间隔。 然后通过根据基尼指数标准选择属性来执行拆分。

         这种方法也适用于多分类特征变量，其中分类属性的每个值对应于分割的一个分支。

1.4 数值因变量（target）的决策树

        为了处理数值因变量，拆分标准从基尼指数更改为更适合数字属性的度量。

         具体而言，使用数值因变量的方差代替基尼指数。 较低的方差是更可取的，因为这意味着节点包含有区别地映射到因变量局部的训练实例。

         叶节点中的平均值，或接一个线性回归模型，用于对叶节点进行预测

1.5 剪枝

        在许多情况下，需要执行剪枝以减少过拟合。

        在这种情况下，在树构建阶段不使用全部，只使用部分训练数据。

         然后，在保留的训练数据上测试剪枝的效果。 如果节点的移除提高了对保留数据的决策树预测的准确性，则对该节点进行剪枝。

         此外，也可以使用拆分标准的其他变体，例如错误率和熵。

2 将决策树延伸到协同过滤

2.1 主要挑战

        将决策树扩展到协同过滤的主要挑战是预测条目和观察条目没有以列方式作为特征和类变量清楚地分开。

        此外，评分矩阵非常稀疏，其中大部分条目都丢失了。这在树构建阶段对训练数据进行分层划分带来了挑战。

        此外，由于协同过滤中的因变量和自变量（项目）没有明确划分，决策树应该预测什么项目？

2.2 解决“应该预测什么”

        通过构建单独的决策树来预测每个项目的评分。

         考虑具有 m 个用户和 n 个项目的 m × n 评级矩阵 R。 需要通过将每个属性视为因变量，其余属性视为自变量来构建单独的决策树。

        因此，构建的决策树的数量等于属性/item的数量n。 

        但在这种考虑下，缺少自变量的问题更难解决。

         考虑将特定项目（例如特定电影）用作拆分属性的情况。 所有评分小于阈值的用户都被分配到树的一个分支，而评分大于阈值的用户被分配到另一个分支。

         由于评分矩阵是稀疏的，因此大多数用户不会为此项目指定评分。

        这些用户应该分配到哪个分支？ 从逻辑和直观上看，应将此类用户分配给两个分支。

        然而，在这种情况下，决策树不再是严格划分。 根据这种方法，测试实例将映射到决策树中的多个路径，并需要将来自各个路径的可能相互冲突的预测组合成单个预测。

2.3 使用降维的思路

        第二种（也是更合理的）方法是使用推荐系统笔记： 基于邻居的协同过滤问题 中的降维中讨论的降维方法创建数据的低维表示。

        考虑需要预测第 j 个项目的评分的场景。一开始，m × (n − 1) 维的 评分矩阵，不包括第j 列，被转换成一个低维的m × d 表示，其中d远小于n − 1，低秩矩阵所有元素都有数值。

        然后，我们就可以将问题视为标准分类或回归问题，此简化表示用于构建第 j 个项目的决策树。

        通过将 j 的值从 1 更改为 n 来重复此方法，以构建总共 n 个决策树。因此，第 j 个决策树仅用于预测第 j 个项目的评分。 

        值得注意的是，这种将降维与分类模型相结合的更广泛方法不仅限于决策树。 将此方法与几乎任何分类模型结合使用相对容易。         

        参考资料 Sci-Hub | Recommender Systems | 10.1007/978-3-319-29659-3