数据结构与算法之深入解析整数转罗马数字的求解思路与算法示例

Posted 2022-01-09 Forever_wj

一、题目描述

• 罗马数字包含以下七种字符： I， V， X， L，C，D 和 M：

字符	数值
I	1
V	5
X	10
L	50
C	100
D	500
M	1000

• 例如， 罗马数字 2 写做 II ，即为两个并列的 1；12 写做 XII ，即为 X + II；27 写做 XXVII, 即为 XX + V + II 。
• 通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV；数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4 ；同样地，数字 9 表示为 IX；这个特殊的规则只适用于以下六种情况：
• • I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9；
• • X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90；
• • C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900；
• 现在给你一个整数，将其转为罗马数字。
• 示例 1:

输入: num = 3
输出: "III"

• 示例 2:

输入: num = 4
输出: "IV"

• 示例 3:

输入: num = 9
输出: "IX"

• 示例 4:

输入: num = 58
输出: "LVIII"
解释: L = 50, V = 5, III = 3

• 示例 5:

输入: num = 1994
输出: "MCMXCIV"
解释: M = 1000, CM = 900, XC = 90, IV = 4

二、题目分析

① 罗马数字符号

• 罗马数字由 7 个不同的单字母符号组成，每个符号对应一个具体的数值。此外，减法规则（如问题描述中所述）给出了额外的 6 个复合符号，这给了我们总共 13 个独特的符号（每个符号由 1 个或 2 个字母组成），如下所示：

M -> 1000
D -> 500
C -> 100
L -> 50
X -> 10
V -> 5
I -> 1

CM -> 900
CD -> 400
XC -> 90 
XL -> 40 
IX -> 9
IV -> 4

② 罗马数字的唯一表示法

• 从一个例子入手，考虑 140 的罗马数字表示，下面哪一个是正确的？

L + L + XL = 50 + 50 + 40 = 140
C + X + X + X + X = 100 + 10 + 10 + 10 + 10 = 140
C + XL = 100 + 40 = 140
XC + L = 90 + 50 = 140
XL + XL + XL + X + X = 40 + 40 + 40 + 10 + 10 = 140
C + X + X + V + V + V + V = 100 + 10 + 10 + 5 + 5 + 5 + 5 = 140

• 我们用来确定罗马数字的规则是：对于罗马数字从左到右的每一位，选择尽可能大的符号值。对于 140，最大可以选择的符号值为 C=100；接下来，对于剩余的数字 40，最大可以选择的符号值为 XL=40；因此，140 的对应的罗马数字为 C + XL = CXL。

三、算法示例

① 模拟

• 思路：
• • 根据罗马数字的唯一表示法，为了表示一个给定的整数 num，我们寻找不超过 num 的最大符号值，将 num 减去该符号值，然后继续寻找不超过 num 的最大符号值，将该符号拼接在上一个找到的符号之后，循环直至 num 为 0，最后得到的字符串即为 num 的罗马数字表示。
• • 编程时，可以建立一个数值-符号对的列表 valueSymbols，按数值从大到小排列，遍历 valueSymbols 中的每个数值-符号对，若当前数值 value 不超过 num，则从 num 中不断减去 value，直至 num 小于 value，然后遍历下一个数值-符号对；若遍历中 num 为 0 则跳出循环。
• 算法示例：
• • C 代码：

const int values[] = 1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1;
const char* symbols[] = "M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I";

char* intToRoman(int num) 
    char* roman = malloc(sizeof(char) * 16);
    roman[0] = '\\0';
    for (int i = 0; i < 13; i++) 
        while (num >= values[i]) 
            num -= values[i];
            strcpy(roman + strlen(roman), symbols[i]);
        
        if (num == 0) 
            break;
        
    
    return roman;

• • Python 代码：

class Solution:

    VALUE_SYMBOLS = [
        (1000, "M"),
        (900, "CM"),
        (500, "D"),
        (400, "CD"),
        (100, "C"),
        (90, "XC"),
        (50, "L"),
        (40, "XL"),
        (10, "X"),
        (9, "IX"),
        (5, "V"),
        (4, "IV"),
        (1, "I"),
    ]

    def intToRoman(self, num: int) -> str:
        roman = list()
        for value, symbol in Solution.VALUE_SYMBOLS:
            while num >= value:
                num -= value
                roman.append(symbol)
            if num == 0:
                break
        return "".join(roman)

• 复杂度分析：
• • 时间复杂度：O(1)，由于 valueSymbols 长度是固定的，且这 13 字符中的每个字符的出现次数均不会超过
    3，因此循环次数有一个确定的上限。对于本题给出的数据范围，循环次数不会超过 15 次；
• • 空间复杂度：O(1)。

② 硬编码数字

• 思路：
• • 回顾上文中列出的 13 个符号，可以发现：
• • • 千位数字只能由 M 表示；百位数字只能由 C，CD，D 和 CM 表示；
• • • 十位数字只能由 X，XL，L 和 XC 表示；
• • • 个位数字只能由 I，IV，V 和 IX 表示。
• • 这恰好把这 13 个符号分为四组，且组与组之间没有公共的符号。因此，整数 num 的十进制表示中的每一个数字都是可以单独处理的。
• • 进一步地，我们可以计算出每个数字在每个位上的表示形式，整理成一张硬编码表，如下图所示，其中 0 对应的是空字符串。

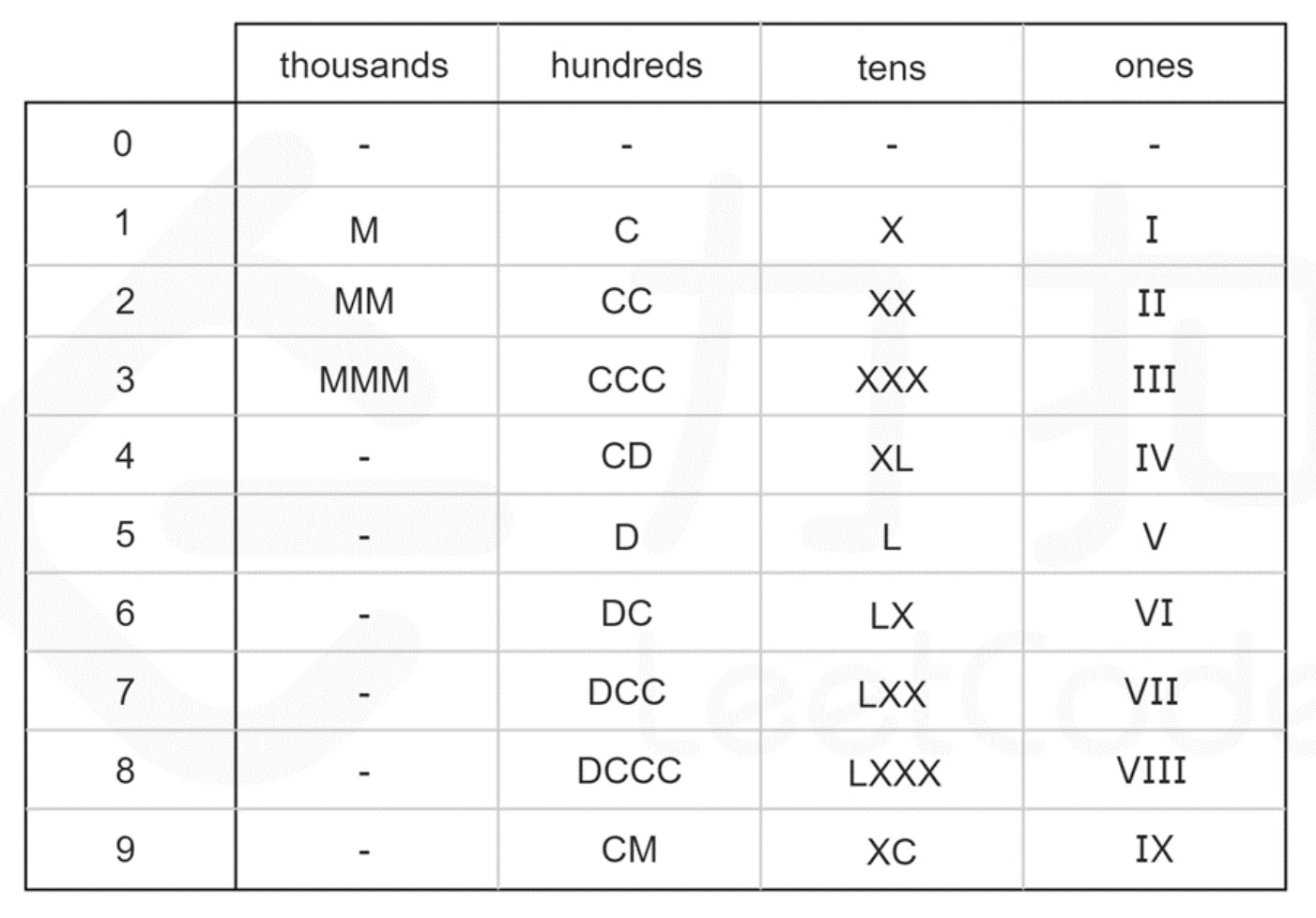
• • 利用模运算和除法运算，可以得到 num 每个位上的数字：

thousands_digit = num / 1000
hundreds_digit = (num % 1000) / 100
tens_digit = (num % 100) / 10
ones_digit = num % 10

• • 最后，根据 num 每个位上的数字，在硬编码表中查找对应的罗马字符，并将结果拼接在一起，即为 num 对应的罗马数字。
• 算法实现：
• • C 示例：

const char* thousands[] = "", "M", "MM", "MMM";
const char* hundreds[] = "", "C", "CC", "CCC", "CD", "D", "DC", "DCC", "DCCC", "CM";
const char* tens[] = "", "X", "XX", "XXX", "XL", "L", "LX", "LXX", "LXXX", "XC";
const char* ones[] = "", "I", "II", "III", "IV", "V", "VI", "VII", "VIII", "IX";

char* intToRoman(int num) 
    char* roman = malloc(sizeof(char) * 16);
    roman[0] = '\\0';
    strcpy(roman + strlen(roman), thousands[num / 1000]);
    strcpy(roman + strlen(roman), hundreds[num % 1000 / 100]);
    strcpy(roman + strlen(roman), tens[num % 100 / 10]);
    strcpy(roman + strlen(roman), ones[num % 10]);
    return roman;

• • Python 示例：

class Solution:

    THOUSANDS = ["", "M", "MM", "MMM"]
    HUNDREDS = ["", "C", "CC", "CCC", "CD", "D", "DC", "DCC", "DCCC", "CM"]
    TENS = ["", "X", "XX", "XXX", "XL", "L", "LX", "LXX", "LXXX", "XC"]
    ONES = ["", "I", "II", "III", "IV", "V", "VI", "VII", "VIII", "IX"]

    def intToRoman(self, num: int) -> str:
        return Solution.THOUSANDS[num // 1000] + \\
            Solution.HUNDREDS[num % 1000 // 100] + \\
            Solution.TENS[num % 100 // 10] + \\
            Solution.ONES[num % 10]

• 复杂度分析：
• • 时间复杂度：O(1)，计算量与输入数字的大小无关；
• • 空间复杂度：O(1)。