数据结构与算法之深入解析罗马数字转整数的求解思路与算法示例

Posted 2022-01-09 Forever_wj

一、题目描述

• 罗马数字包含以下七种字符：I， V， X， L，C，D 和 M：

字符	数值
I	1
V	5
X	10
L	50
C	100
D	500
M	1000

• 例如， 罗马数字 2 写做 II ，即为两个并列的 1 ；12 写做 XII ，即为 X + II ；27 写做 XXVII, 即为 XX + V + II 。
• 通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4。同样地，数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况：
• • I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9；
• • X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90；
• • C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900；
• 给定一个罗马数字，将其转换成整数。
• 示例 1:

输入: s = "III"
输出: 3

• 示例 2:

输入: s = "IV"
输出: 4

• 示例 3:

输入: s = "IX"
输出: 9

• 示例 4:

输入: s = "LVIII"
输出: 58
解释: L = 50, V= 5, III = 3

• 示例 5:

输入: s = "MCMXCIV"
输出: 1994
解释: M = 1000, CM = 900, XC = 90, IV = 4

二、求解算法

① 模拟

• 思路：
• • 通常情况下，罗马数字中小的数字在大的数字的右边，若输入的字符串满足该情况，那么可以将每个字符视作一个单独的值，累加每个字符对应的数值即可。例如 XXVII 可视作 X+X+V+I+I=10+10+5+1+1=27。
• • 若存在小的数字在大的数字的左边的情况，根据规则需要减去小的数字，对于这种情况，我们也可以将每个字符视作一个单独的值，若一个数字右侧的数字比它大，则将该数字的符号取反。例如 XIV 可视作 X−I+V=10−1+5=14。
• 算法实现：
• • C 示例：

int romanToInt(char* s) 
    int symbolValues[26];
    symbolValues['I' - 'A'] = 1;
    symbolValues['V' - 'A'] = 5;
    symbolValues['X' - 'A'] = 10;
    symbolValues['L' - 'A'] = 50;
    symbolValues['C' - 'A'] = 100;
    symbolValues['D' - 'A'] = 500;
    symbolValues['M' - 'A'] = 1000;
    int ans = 0;
    int n = strlen(s);
    for (int i = 0; i < n; ++i) 
        int value = symbolValues[s[i] - 'A'];
        if (i < n - 1 && value < symbolValues[s[i + 1] - 'A']) 
            ans -= value;
         else 
            ans += value;
        
    
    return ans;

• • Python 示例：

class Solution:

    SYMBOL_VALUES = 
        'I': 1,
        'V': 5,
        'X': 10,
        'L': 50,
        'C': 100,
        'D': 500,
        'M': 1000,
    

    def romanToInt(self, s: str) -> int:
        ans = 0
        n = len(s)
        for i, ch in enumerate(s):
            value = Solution.SYMBOL_VALUES[ch]
            if i < n - 1 and value < Solution.SYMBOL_VALUES[s[i + 1]]:
                ans -= value
            else:
                ans += value
        return ans

• 复杂度分析：
• • 时间复杂度：O(n)，其中 n 是字符串 s 的长度；
• • 空间复杂度：O(1)。

② 简单求解

• 按照题目的描述，可以总结如下规则：
• • 罗马数字由 I,V,X,L,C,D,M 构成；
• • 当小值在大值的左边，则减小值，如 IV=5-1=4；
• • 当小值在大值的右边，则加小值，如 VI=5+1=6；
• • 由上可知，右值永远为正，因此最后一位必然为正。
• 一言蔽之，把一个小值放在大值的左边，就是做减法，否则为加法。

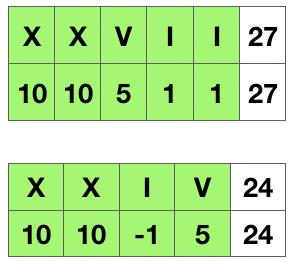
• 在代码实现上，可以往后看多一位，对比当前位与后一位的大小关系，从而确定当前位是加还是减法。当没有下一位时，做加法即可。
• 也可保留当前位的值，当遍历到下一位的时，对比保留值与遍历位的大小关系，再确定保留值为加还是减，最后一位做加法即可。
• Java 示例：

import java.util.*;

class Solution 
    public int romanToInt(String s) 
        int sum = 0;
        int preNum = getValue(s.charAt(0));
        for(int i = 1;i < s.length(); i ++) 
            int num = getValue(s.charAt(i));
            if(preNum < num) 
                sum -= preNum;
             else 
                sum += preNum;
            
            preNum = num;
        
        sum += preNum;
        return sum;
    
    
    private int getValue(char ch) 
        switch(ch) 
            case 'I': return 1;
            case 'V': return 5;
            case 'X': return 10;
            case 'L': return 50;
            case 'C': return 100;
            case 'D': return 500;
            case 'M': return 1000;
            default: return 0;