第十二届蓝桥杯C++组省赛B组题解(A -- B)

Posted 2022-01-08 黑炭保安

目录

• A.空间
• B.卡片
• C.直线
• D.货物摆放
• E.路径
• G.砝码称重

A.空间

已知:
1MB = 1024KB
1KB = 1024B

一个数组单元占用4B的字节内存，所以答案为

256 * 1024 * 1024 / 4 = 67108864

B.卡片

用一个数组存每种卡片还有多少张，再用一个循环遍历每个要凑的数，当卡片数不够了就输出答案

int a[10] = 2021, 2021, 2021, 2021, 2021, 2021, 2021, 2021, 2021, 2021;

int main()

	for (int i = 1; i; i ++ )
		int t = i;
		while (t)
			int s = t % 10;
			if(a[s] >= 1) a[s] --;
			else
				cout << i - 1 << endl;
				return 0;
			
			t /= 10;
		
	 	

答案：3181

C.直线

用四层循环枚举所有点(x1, y1), (x2, y2)
然后用公式计算斜率和截距
k = (y2-y1) / (x2-x1)
b = (x2 * y1 - y2 * x1) / (x2 - x1)
再用map / set储存一下每条直线的斜率和截距。需要注意的是要特判斜率为0的时候

typedef pair<double, double>PII;

map<PII, bool>mp;

int main()

	for (int x1 = 0; x1 < 20; x1 ++ )
		for (int y1 = 0; y1 < 21; y1 ++ )
			for (int x2 = 0; x2 < 20; x2 ++ )
				for (int y2 = 0; y2 < 20; y2 ++ )
					if(x1 == x2) continue;
					double k = (double)(y2 - y1) / (double)(x2 - x1);
					double b = (double)(x2 * y1 - y2 * x1) / (x2 - x1);
					mp[k, b] = true;	
				
			
		
	
	
	cout << mp.size() + 21;

答案：40257

D.货物摆放

最简单的思路肯定是 两层for枚举，暴力求解。但是这样做题目给的数据实在太大了，一定会超时，所以就要换思路。
首先令N = 2021401820211048
要三个数相乘等于N，那么这三个数一定是N的约数，所以我们可以枚举所有三个约数相乘的结果，如果等于N， 答案就+1

试除法求约数

void get_divisors()

	for (int i = 1; i <= N / i; i ++ )
		if(N % i == 0)
        
            if(i == N / i) a[t ++] = i;
            else
                a[t ++] = i;
                a[t ++] = N / i; 
            
         
	

枚举三个约数相乘 （注意，一定要先把数组排序）

sort(a, a + t);
int ans = 0;
for (int i = 0; i < t; i ++ )
		for (int j = 0; j < t; j ++ )
			if(a[i] * a[j] > N) break;
			for (int k = 0; k < t; k ++ )
				if(a[i] * a[j] * a[k] == N) ans ++;
			
		
	

答案：2430

E.路径

很明显一道最短路的问题 (我当时用bfs跑了一个多小时暴出来的 ）
：先建图，再跑一边dijkstra / spfa / floyd就可以
知识点：两个数a, b的最大公倍数 = ( a * b / (a,b的最大公约数) )
而最大公约数可以用函数__gcd(a,b)来求
所以边权为a * b / __gcd(a,b)

建图：

void add(int a, int b)

	int c;
	c = a * b / __gcd(a, b);
	e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;


int main()

	memset(h, -1, sizeof h);
	for (int i = 1; i < 2021; i ++ )
		for (int j = i; j <= i + 21; j ++ )
			add(i, j);
		
	

再用最短路模板跑一遍
我用的是spfa 毕竟万能

void spfa()

	memset(dist, 0x3f, sizeof dist);
	dist[1] = 0;
	st[1] = true;
	queue<int>q;
	q.push(1);
	while (q.size())
	
		int t = q.front();
		q.pop();
		
		st[t] = false;
		
		for (int i = h[t]; i != -1; i = ne[i])
			int j = e[i];
			if(dist[j] > dist[t] + w[i])
				dist[j] = dist[t] + w[i];
				if(!st[j])
					st[j] = true;
					q.push(j);
				
			
		
	
	cout << dist[2021];

答案：10266837

F.时间显示

首先 这题只要求显示小时，分钟，秒钟。 那么我们就要先去掉每个整天的毫秒时间

	long long n;
	cin >> n;
	int days = 1000 * 60 * 60 * 24;
	n -= n / days * days; 

这样我们得到的时间就一定是从00：00开始不超过24小时的时间
然后就是很简单的模拟了

	int s = n / 1000; //多少秒 
	int min = s / 60; //多少分钟 
	int hour = min / 60; //多少小时 
	
	s %= 60;
	min %= 60;
	hour %= 24;
	
	if(hour < 10) cout << 0;
	cout << hour << ':';
	if(min < 10) cout << 0;
	cout << min << ':';
	if(s < 10) cout << 0;
	cout << s;

G.砝码称重

一道DFS / DP 的题 但是DFS能拿一半的分，所以这里只讲DP的解法

首先我们对于每个砝码，有三种选法：放左边，放右边，不放。这样看就是一个简单的01背包问题

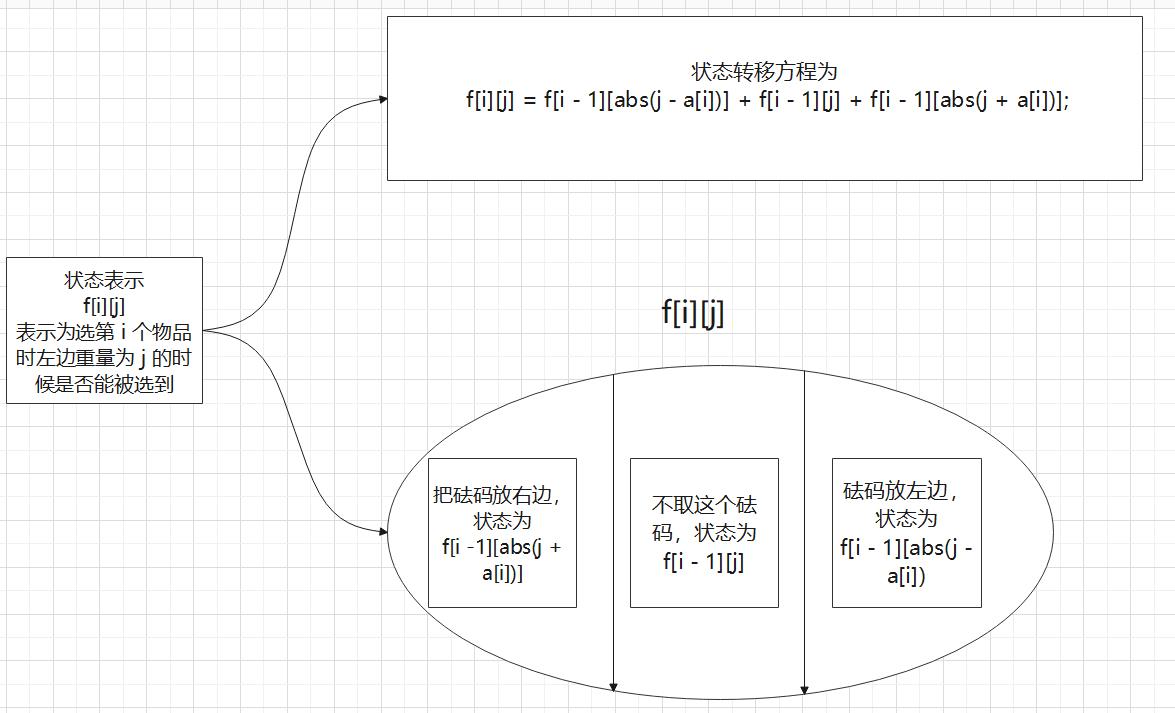
核心代码

	cin >> n; 
	int sum = 0;
	for (int i = 1; i <= n; i ++ )
	    cin >> a[i];
	    sum += a[i];
	
	
	f[0][0] = 1;
	for (int i = 1; i <= n; i ++ )
	    for (int j = 0; j <= sum; j ++ )
	        f[i][j] = f[i - 1][abs(j - a[i])] + f[i - 1][j] + f[i - 1][abs(j + a[i])];
	    
	

如果能选到这个重量，那么f[i][j]的值就不为0，所以答案就为

	int ans = 0;
	for (int i = 1; i <= sum; i ++ )
	        if(f[n][i]) ans ++;
	
	cout << ans;