第十二届蓝桥杯省赛第一场C++ A/B/C组 真题题解(详细讲解 + 代码分析)看这篇就够了~~~~
Posted 满天星!
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了第十二届蓝桥杯省赛第一场C++ A/B/C组 真题题解(详细讲解 + 代码分析)看这篇就够了~~~~相关的知识,希望对你有一定的参考价值。
第十二届蓝桥杯省赛第一场C++ A/B/C组 真题题解(详细讲解 + 代码分析)
空间

AC代码
#include<bits/stdc++.h>
using namespace std;
int main()
cout<<256*1024*1024/4<<endl;
return 0;
// 答案 67108864
卡片

AC代码
#include<bits/stdc++.h>
using namespace std;
int a[15];
bool check(int x)
while(x)
int t=x%10;
x/=10;
if(--a[t]<0) return false;
return true;
int main()
for(int i=0;i<=9;i++) a[i]=2021;
for(int i=1;;i++)
if(!check(i))
cout<<i-1<<endl;
return 0;
return 0;
// 答案 3181
直线

AC代码
#include<bits/stdc++.h>
using namespace std;
const int N=200000;
int n;
struct Line
double k,b;
bool operator<(const Line& t) const
if (k!=t.k) return k<t.k;
return b<t.b;
l[N];
int main()
for (int x1=0;x1<20;x1++ )
for (int y1=0;y1<21;y1++ )
for (int x2=0;x2<20;x2++ )
for (int y2=0;y2<21;y2++ )
if (x1!=x2)
double k=(double)(y2 - y1)/(x2 - x1);
double b=y1-k*x1;
l[n++]=k,b;
sort(l,l+n);
int ans=1;
for (int i=1; i<n;i++)
if (abs(l[i].k-l[i-1].k)>1e-8||abs(l[i].b-l[i-1].b)>1e-8)ans++ ;
cout <<ans+20<<endl;
return 0;
//答案:40257
货物摆放

AC代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
ll n;
cin>>n;
vector<ll>d;
for(ll i=1;i*i<=n;i++)
if(n%i==0)
d.push_back(i);
if(n/i!=i) d.push_back(n/i);
int ans=0;
for(auto l:d)
for(auto w:d)
for(auto h:d)
if(l*w*h==n) ans++;
cout<<ans<<endl;
return 0;
// 答案 2430
路径

AC代码
#include<bits/stdc++.h>
using namespace std;
const int N=2200,M=N*50;
int h[N],e[M],w[M],ne[M],q[N],dis[N];
int n,idx;
bool st[N];
void add(int a,int b,int x) 添加一条边a->b,边权为x
e[idx]=b;
w[idx]=x;
ne[idx]=h[a];
h[a]=idx++;
int gcd(int a,int b)
return b?gcd(b,a%b):a;
//求1号点到n号点的最短路距离
void spfa()
int hh=0,tt=0;
memset(dis,0x3f,sizeof dis);
dis[1]=0;
q[tt++]=1;
st[1]=true;
while(hh!=tt)
int t=q[hh++];
if(hh==N) hh=0;
st[t]=true;
for(int i=h[t];i!=-1;i=ne[i])
int j=e[i];
if(dis[j]>dis[t]+w[i])
dis[j]=dis[t]+w[i];
if(!st[j])
q[tt++]=j;
if(tt==N) tt=0;
st[j]=true;
int main()
n=2021;
memset(h,-1,sizeof h);
for(int i=1;i<=n;i++)
for(int j=max(1,i-21);j<=min(n,i+21);j++)
int d=gcd(i,j);
add(i,j,i*j/d);
spfa();
cout<<dis[n]<<endl;
return 0;
//答案 10266837
时间显示
题目描述
小蓝要和朋友合作开发一个时间显示的网站。
在服务器上,朋友已经获取了当前的时间,用一个整数表示,值为从 1970 年 1 月 1 日 00:00:00 到当前时刻经过的毫秒数。
现在,小蓝要在客户端显示出这个时间。
小蓝不用显示出年月日,只需要显示出时分秒即可,毫秒也不用显示,直接舍去即可。
给定一个用整数表示的时间,请将这个时间对应的时分秒输出。
输入格式
输入一行包含一个整数,表示时间。
输出格式
输出时分秒表示的当前时间,格式形如 HH:MM:SS,其中 HH 表示时,值为 0 到 23,MM 表示分,值为 0 到 59,SS 表示秒,值为 0 到 59。
时、分、秒不足两位时补前导 0。
数据范围
对于所有评测用例,给定的时间为不超过 1018 的正整数。
输入样例1:
46800999
输出样例1:
13:00:00
输入样例2:
1618708103123
输出样例2:
01:08:23
思路:
1.这里需要注意,一秒 = 1000毫秒
2.这里的输入的数据超过了int的范围,需要用long long进行存储
AC代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
ll time;
cin>>time;
ll h=(time/1000/60/60)%24;
ll m=(time/1000/60)%60;
ll s=(time/1000)%60;
printf("%02lld:%02lld:%02lld\\n",h,m,s);
return 0;
砝码去重
题目描述:
你有一架天平和 N 个砝码,这 N 个砝码重量依次是 W1,W2,⋅⋅⋅,WN。
请你计算一共可以称出多少种不同的正整数重量?
注意砝码可以放在天平两边。
输入格式
输入的第一行包含一个整数 N。
第二行包含 N 个整数:W1,W2,W3,⋅⋅⋅,WN。
输出格式
输出一个整数代表答案。
数据范围
对于 50% 的评测用例,1≤N≤15。
对于所有评测用例,1≤N≤100,N 个砝码总重不超过 105。
输入样例:
3
1 4 6
输出样例:
10
样例解释
能称出的 10 种重量是:1、2、3、4、5、6、7、9、10、11。
1 = 1;
2 = 6 − 4 (天平一边放 6,另一边放 4);
3 = 4 − 1;
4 = 4;
5 = 6 − 1;
6 = 6;
7 = 1 + 6;
9 = 4 + 6 − 1;
10 = 4 + 6;
11 = 1 + 4 + 6。
思路:
dp
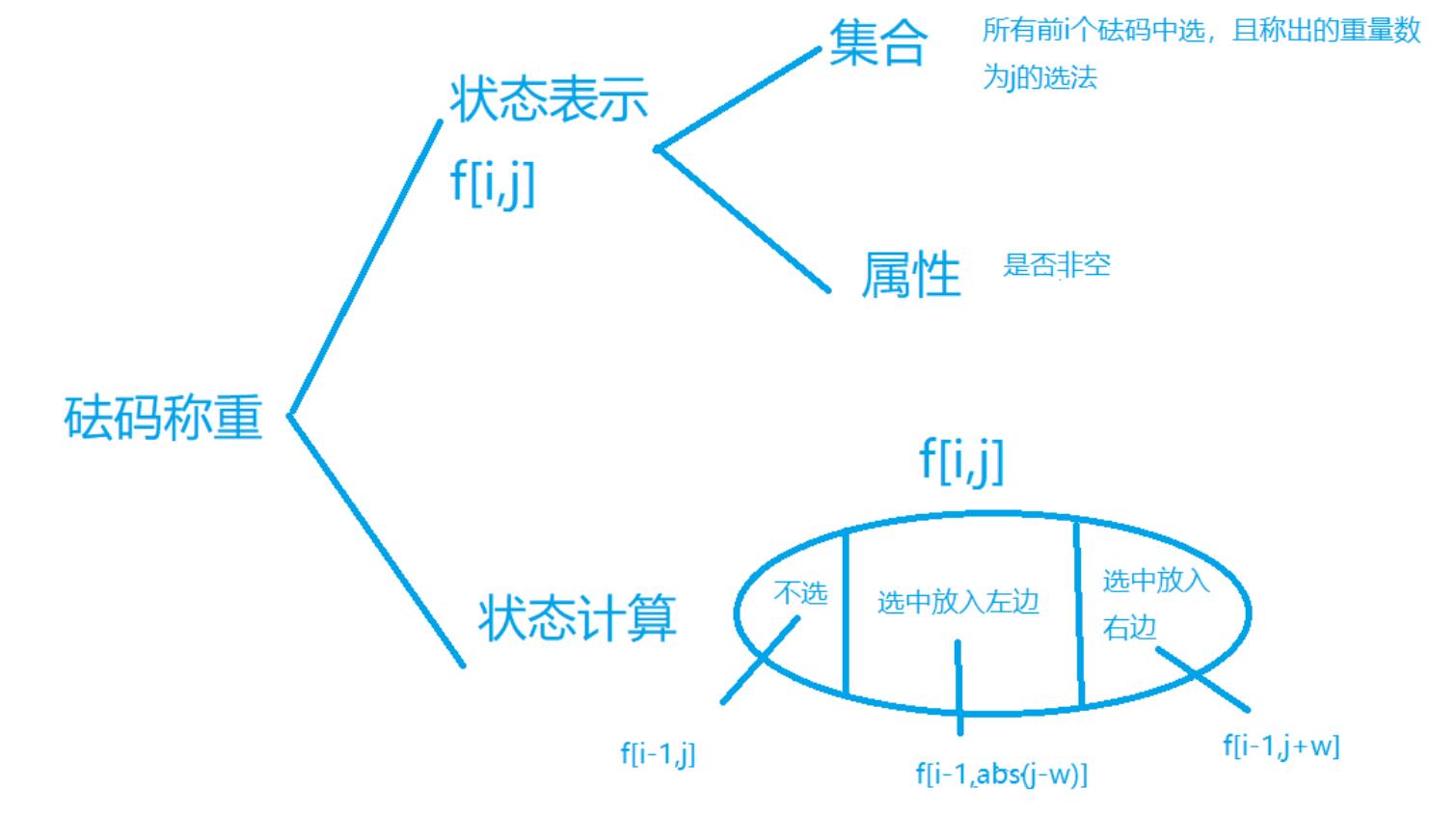
AC代码
#include<bits/stdc++.h>
using namespace std;
const int N=110,M=2e5+10;
bool f[N][M];
int w[N],sum,n;
int main()
cin>>n;
for(int i=1;i<=n;i++) cin>>w[i],sum+=w[i];
f[0][0]=true;
for(int i=1;i<=n;i++)
for(int j=0;j<=sum;j++)
//只要有一个非空,f[i][j]就非空
f[i][j]=f[i-1][j]||f[i-1][abs(j-w[i])]||f[i-1][j+w[i]];
int res=0;
for(int i=1;i<=sum;i++)
if(f[n][i]) res++; //不为零说明可以选出这个质量的砝码
cout<<res<<endl;
return 0;
杨辉三角
题目描述:
下面的图形是著名的杨辉三角形:
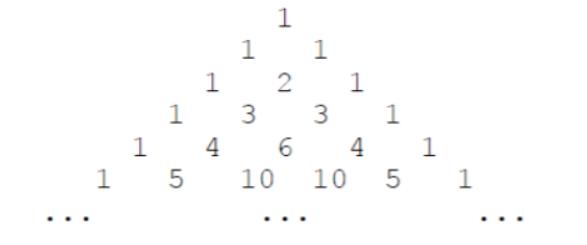
如果我们按从上到下、从左到右的顺序把所有数排成一列,可以得到如下数列:
1, 1, 1, 1, 2, 1, 1, 3, 3, 1, 1, 4, 6, 4, 1, …
给定一个正整数 N,请你输出数列中第一次出现 N 是在第几个数?
输入格式
输入一个整数 N。
输出格式
输出一个整数代表答案。
数据范围
对于 20% 的评测用例,1≤N≤10;
对于所有评测用例,1≤N≤109。
输入样例:
6
输出样例:
13
思路
//组合数和杨辉三角:第i行第j列的数都是组合数C(i, j) (i,j从0开始)
// C(n, 1) = n --> 对应从左向右看斜着的第二列! ---> 一定有解
// 由于杨辉三角左右对称(C(a, b) == C(a, a-b)),
// 又由于找第一次出现,因此一定在左边,右边可以直接删掉!
// C(2n, n) n最大1e9,C(34, 17) > 1e9, C(32, 16) < 1e9,因此只要枚举前16个斜行即可
// 性质:
// 1. 每一斜行从上到下递增
// 2. 每一横行从中间到两边依次递减
// 因此我们直接从中间对称轴倒序二分找起即可
// C(r, k)对应的顺序值为:(r + 1) * r / 2 + k + 1
// 二分的左右端点:l:2k,r:max(n, l)
// 右端点一定不能比左端点小!
// 特例:否则当n=1时,会出问题!
AC代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n;
ll C(int a,int b)
ll res=1;
for(int i=a,j=1;j<=b;i--,j++)
res=res*i/j;
// 大于n已无意义,且防止爆long long
if(res>n) return res;
return res;
bool check(int k)
// 二分该斜行,找到大于等于该值的第一个数
// 左边界2k,右边界为max(l, n)取二者最大即可
ll l=k*2,r=max((ll)n,l);
while(l<r)
ll mid=l+r>>1;
if(C(mid,k)>=n) r=mid;
else l=mid+1;
if(C(r,k)!=n) return false;
// C(r, k)的从0开始的顺序
cout<<r*(r+1)/2+k+1<<endl;
return true;
int main()
cin>>n;
for(int k=16;;k--)
if(check(k)) break;
return 0;
左孩子右兄弟
题目描述:
对于一棵多叉树,我们可以通过 “左孩子右兄弟” 表示法,将其转化成一棵二叉树。
如果我们认为每个结点的子结点是无序的,那么得到的二叉树可能不唯一。
换句话说,每个结点可以选任意子结点作为左孩子,并按任意顺序连接右兄弟。
给定一棵包含 N 个结点的多叉树,结点从 1 至 N 编号,其中 1 号结点是根,每个结点的父结点的编号比自己的编号小。
请你计算其通过 “左孩子右兄弟” 表示法转化成的二叉树,高度最高是多少。
注:只有根结点这一个结点的树高度为 0。
例如如下的多叉树:
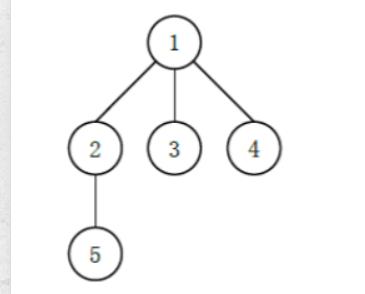
可能有以下 3 种 (这里只列出 3 种,并不是全部) 不同的 “左孩子右兄弟”表示:
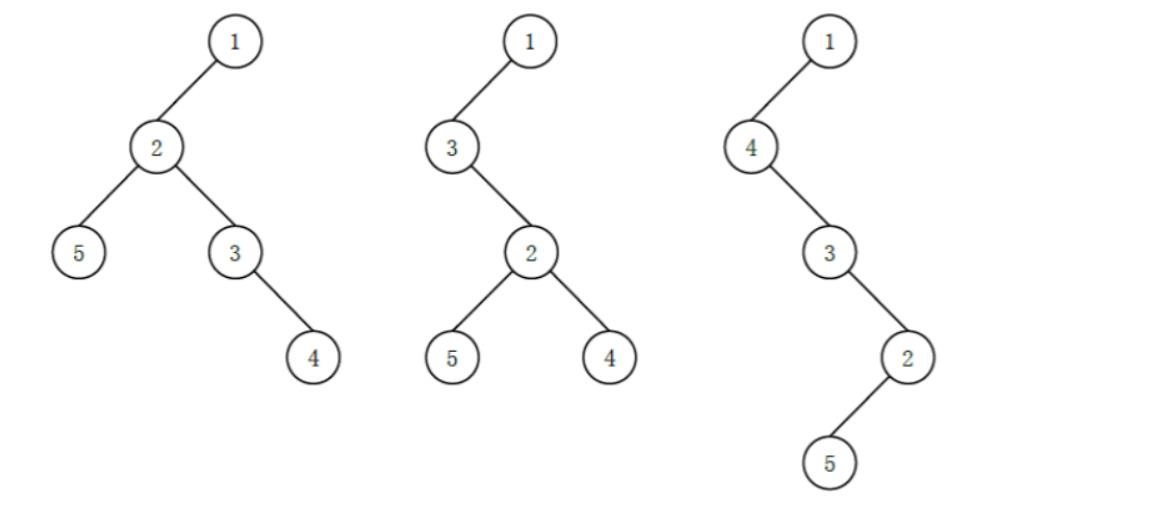
其中最后一种高度最高,为 4。
输入格式
输入的第一行包含一个整数 N。
以下 N−1 行,每行包含一个整数,依次表示 2 至 N 号结点的父结点编号。
输出格式
输出一个整数表示答案。
数据范围
对于 30% 的评测用例,1≤N≤20;
对于所有评测用例,1≤N≤105。
输入样例:
5
1
1
1
2
输出样例:
4
思路:
状态表示:f[u]表示的是以u为根节点的树的最大高度
状态计算: f[u]=max(f[u],f[j]+num[u]);(num[u]表示的是以u为根节点的子节点个数)
用话语描述就是,当前树的高度等于它 与 其子树高度+以这个节点为根的儿子结点数之和取max
对于每一个子树而言,如果想要树的高度最大,那么必须让除了一个儿子外的其他儿子作为兄弟出现。
比如样例 1 号节点有三个儿子,我们让其中一个作为儿子,另外两个作为这个儿子的兄弟(因为作为兄弟可以而增加树的高度),
这样,三个儿子一共可以增加三个高度,然后再看 2 号节点有一个儿子,再加上 1 个高度,答案就是 4 。
递归去做,从最小的子树往上回溯,边回溯边计算f[]就可以得到最高的一棵树了。
AC代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int e[N*2],ne[N*2],h[N],idx;
int f[N];//f[u]表示的是以u为根节点的树的最大高度
int n;
int num[N];//num[u]表示的是以u为根节点的子节点个数
void add(int a,int b)
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
int dfs(int u,int fa)
for(int i=h[u];i!=-1;i=ne[i])
int j=e[i];
if(j!=fa)//保证递归向下的过程不会出现回溯
dfs(j,u);
f