数据结构与算法—查找（树表的查找）

Posted 2022-01-08 之墨_

查找-树表的查找

• 二叉排序树
• • 对于创建二叉树算法的说明：
  • 完整代码实现

二叉排序树

二叉排序树(binary search tree,BST)又称二叉搜索树
其定义为二叉排序树或者是空树
或者是满足以下性质的二叉树
(1)若根结点的左子树非空,则左子树上的所有结点关键字均小于根结点关键字；
(2)若根结点的右子树非空,则右子树上的所有结点关键字均大于根结点关键字；
(3)根结点的左、右子树本身又各是一棵二叉排序树;

上述性质简称二叉排序树性质(BST 性质)
故二叉排序树实际上是满足 BST 性质的二叉树

也就是说,二叉排序树是在二叉树基础上增加了结点值的约束
简而言之：
左结点关键字值 < 父结点关键字值 < 右结点关键字值

如此定义的二叉排序树中,各结点关键字是唯一的
但在实际应用中
不能保证被查找的数据集中各元素的关键字互不相同

所以可将二叉排序树定义中
BST 性质(1)里的“小于”改为“小于等于”
或将 BST 性质(2)里的“大于”改为“大于等于”
甚至修改为左子树关键字大,右子树关键字小

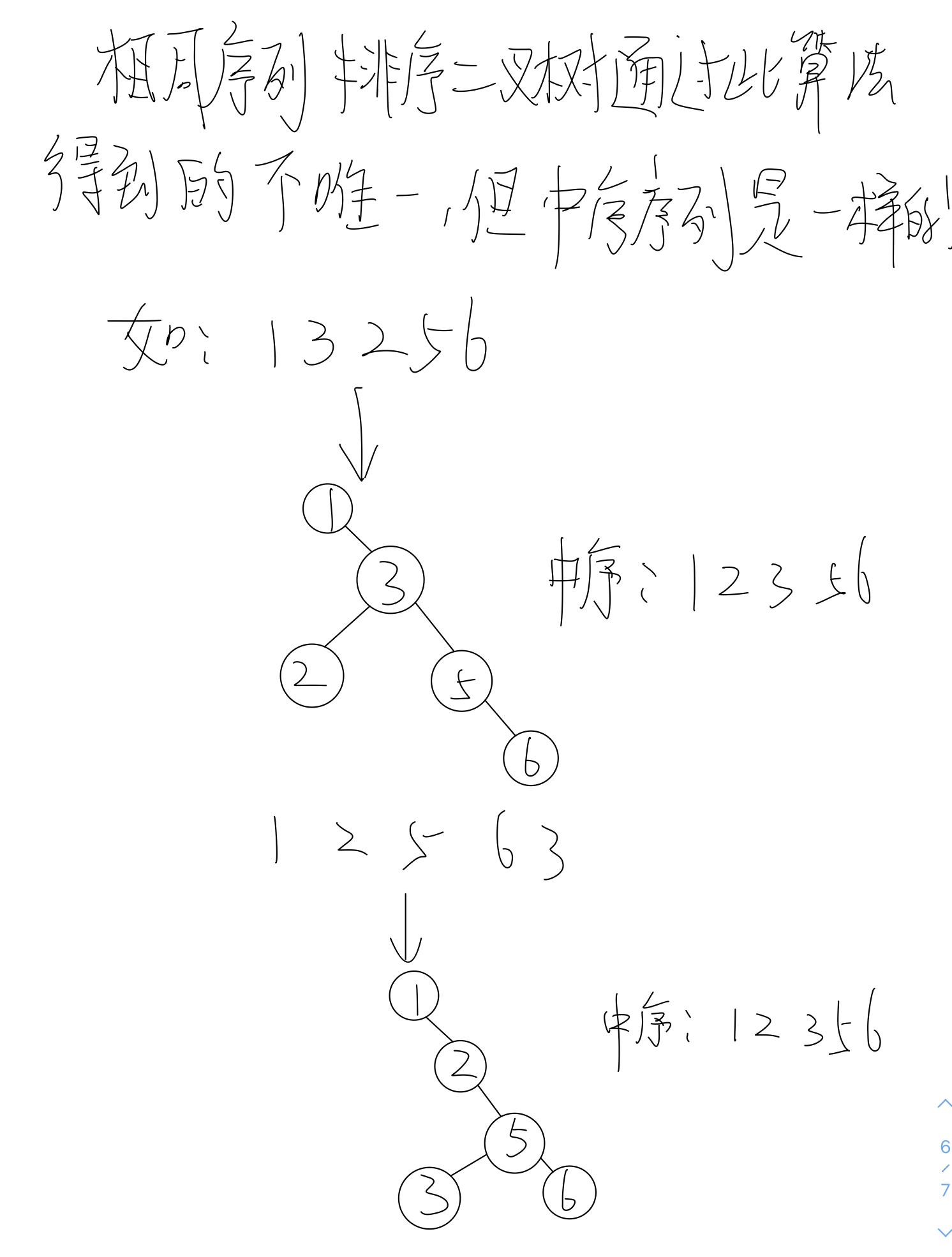
从 BST 性质可推出二叉排序树的另一个重要性质： 按中序遍历该树所得到的中序序列是一个递增有序序列

二叉排序树结点的类型如下

typedef struct node  //元素类型

KeyType key;   //关键字域
InfoType data;  //数据域
struct node *lchild,*rchild;//左右孩子指针
BSTNode;

接下来创建排序二叉树 和 对排序二叉树插入值

其中 创建可用 递归和非递归实现
这里插入就使用递归实现 似乎不用递归有点复杂
并且要注意到排序二叉树的特点
创建排序二叉树时，较大（较小）的值只有在被比较结点左孩子（右孩子）为空时才能直接插入，否则就要和它的左孩子（右孩子）继续比较进行插入！

对于创建二叉树算法的说明：

完整代码实现

#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

using namespace std;

typedef int InfoType;
typedef int KeyType;

typedef struct node  //元素类型

KeyType key;   //关键字域
InfoType data;  //数据域
struct node *lchild,*rchild;//左右孩子指针
BSTNode;

void InitTree(BSTNode *&T)//初始化二叉排序树

	T = (BSTNode*)malloc(sizeof(BSTNode));//创建一个头结点
	T->key = NULL;
	T->lchild = T->rchild = NULL;//头结点指针域和数据域都NULL


void InOrderTraverse(BSTNode *T)//遍历二叉树，中序遍历
///中序遍历
	if(T)
	
		InOrderTraverse(T->lchild);
		printf("%d ",T->data);
		InOrderTraverse(T->rchild);
	


void CreateBSTtree(BSTNode *&T)
///非递归创建排序二叉树
    int a;
    cout<<"输入一个整数：";cin>>a;
    T->data = a;
    BSTNode *p = T;
    if(getchar() == '\\n')
        return;
    while(1)
    
        cin>>a;//要赋给结点的值
        BSTNode *b;
        b = (BSTNode *)malloc(sizeof(BSTNode));
        b->lchild = b->rchild = NULL;//初始化
        b->data = a;
        while(1)
        
            if(b->data > p->data) //新插入的值大于原值
             if(p->rchild != NULL) //p的右孩子已经有结点时
                p = p->rchild;//s和p的右孩子进行比较 继续下一轮循环
            else //右孩子无结点
            
                p->rchild = b;//将s放在p的右孩子上
                break;
            
            else
                if(p->lchild != NULL)
                 p = p->lchild;//s和p的左孩子进行比较 继续下一轮循环
            else
            
                p->lchild = b;//将s放在p的左孩子上
                break;
            
        
        p = T;//让下一个结点继续从头节点开始逐个比较大小
        if(getchar() == '\\n')//敲入回车结束输入
            break;
    


bool InsertTree(BSTNode *&T,int e)
///递归插入结点
    if(T == NULL)  //当T为空即 T的父节点的左或右结点为空 可以插入
    
        T = (BSTNode *)malloc(sizeof(BSTNode));
        T->data = e;
        T->lchild = T->rchild = NULL;
        return true;
    
    else if(e == T->data)  //数据相同 不允许插入
        return false;
    else if(e < T->data)  //小于时  插入他的左结点  并且为空时才能直接插入  否则继续和他的左节点值进行比较
        return InsertTree(T->lchild,e);
    else  //大于就插入 右节点  并且为空时才能直接插入  否则继续和他的右节点值进行比较
        return InsertTree(T->rchild,e);


void CreateTree(BSTNode *&T)//创建二叉排序树
///递归创建排序二叉树
	int a;
	printf("请输入：");
	scanf("%d",&a);
	T->data = a;//将数据填入二叉排序树的根结点
	while(1)//利用循环进行插入操作
	
		scanf("%d",&a);
		InsertTree(T,a);//将数据导入到二叉排序树T中
		if(getchar()=='\\n')//死循环结束条件
			break;
	


int main()

    BSTNode *T;
	InitTree(T);//创建并初始化二叉树
	CreateTree(T);//递归创建排序二叉树
	//CreateBSTtree(T);//非递归创建排序二叉树
	printf("排序后的结果为： ");
	InOrderTraverse(T);//遍历并打印二叉树
	InsertTree(T,6);
    printf("\\n插入6后的结果为： ");
    InOrderTraverse(T);//遍历并打印二叉树