JavaScript归并排序和分治算法

Posted 2022-01-06 永远没有404

欢迎学习交流！！！
持续更新中…
有关排序算法可以查看我之前的博文：冒泡排序和选择排序

文章目录

• 1. 分治算法
• • 分治思想
  • 适用情况
• 2. 归并排序
• • 举例
  • 分析

---

1. 分治算法

       把一个复杂的问题分解两个或更多的相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单的直接解决，原问题的解即子问题的解的合并

分治思想

       将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。（小的问题解决了，大的问题也就解决了）

适用情况

• 规模缩小到一定程度更容易解决
• 问题分解成若干小规模相同子问题， 问题具有最优结构性质
• 小规模问题可以合并求出该问题的解
• 各个子问题相互独立

1. 最优子结构性质。如果问题的最优解所包含的子问题的解也是最优的，我们就称该问题具有最优子结构性质（即满足最优化原理）。最优子结构性质为动态规划算法解决问题提供了重要线索。
2. 无后效性。即子问题的解一旦确定，就不再改变，不受在这之后、包含它的更大的问题的求解决策影响。
3. 子问题重叠性质。子问题重叠性质是指在用递归算法自顶向下对问题进行求解时，每次产生的子问题并不总是新问题，有些子问题会被重复计算多次。动态规划算法正是利用了这种子问题的重叠性质，对每一个子问题只计算一次，然后将其计算结果保存在一个表格中，当再次需要计算已经计算过的子问题时，只是在表格中简单地查看一下结果，从而获得较高的效率。

2. 归并排序

       将待排序的元素分为大小大致相同的集合， 分别对两个子集合进行排序， 最终排序号的子集合合并为有序集合。运用了分而治之的思想（分治法）。

归并排序是八大排序算法其中一种（快速、堆、冒泡、希尔、归并、桶、选择、插入）， 归并采用分而治之的思想对排序序列，分解成不可再分的子序列，再对子序列向上合并

       由上面的动图可以看出，一开始是两个元素开始比较，然后是4个，再然后是8个元素进行比较，这个方法和递归有些相像，其实分治算法一般都是用递归来实现。

       分治是一种解决问题的处理思想，而递归是一种编程技巧

举例

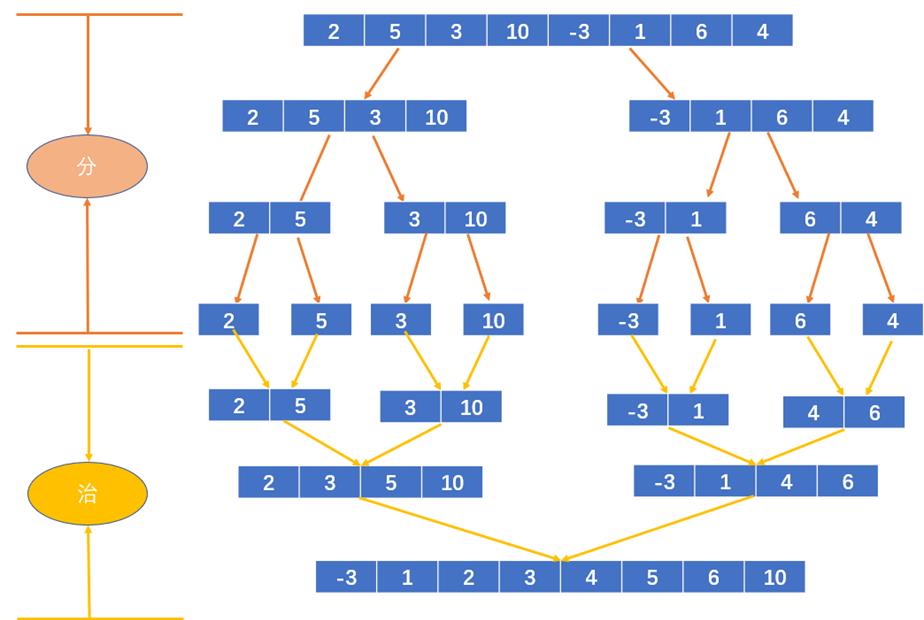
输入数组 [ 2, 5, 3 , 10, -3, 1 , 6 , 4]；初始状态如下：

分治思想如下：

       首先把数组依次折半，分成小的子数组，直到每一个子数组的长度都为1；
       然后合并子数组，在合并的过程中进行排序；

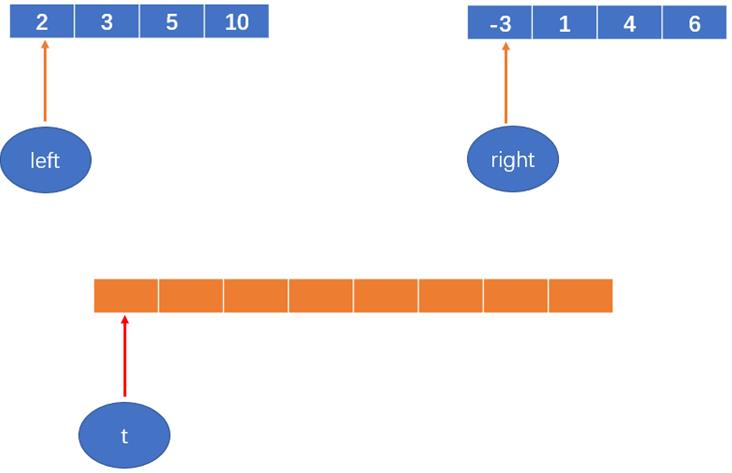
以最后一此合并为例的合并操作：

合并前两个数组：

       定义两个变量left 和 right ，分别赋值为两个数组的首元素的索引；

       初始化一个数组，数组长度为原数组大小；

       再定义一个变量，t，初始化为新开的数组的第一个元素的索引，即0；

如图：

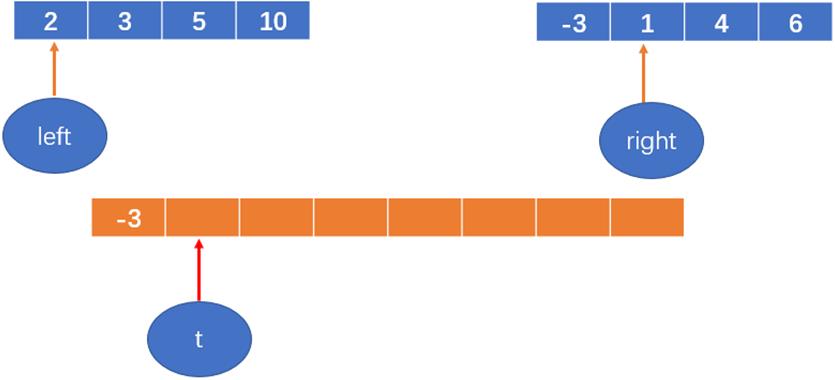
       每次从两个数组中找相对较小的数，填到新开的数组中；

       -3 < 2，将 -3 填到数组中，right++，然后t++；

       1< 2，将1填到数组中，right++，然后t++;

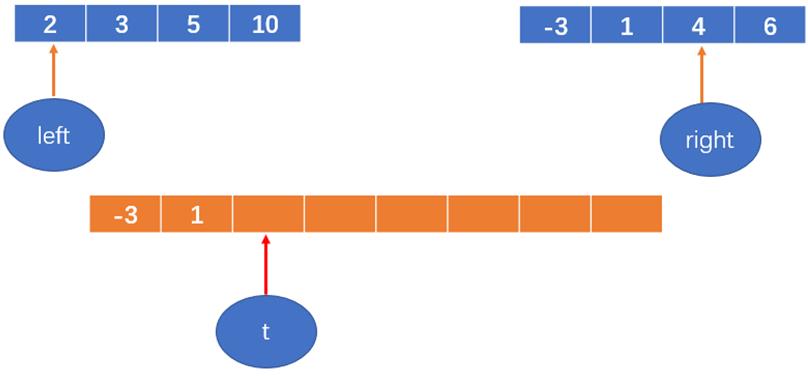
       2 < 4，将2填到数组中，left++，然后t++;

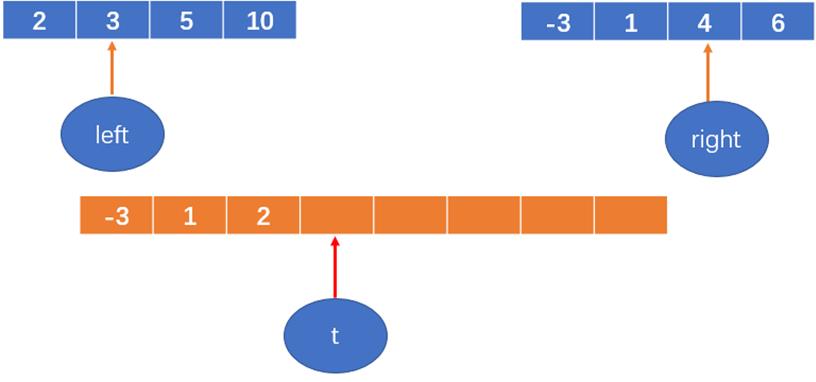
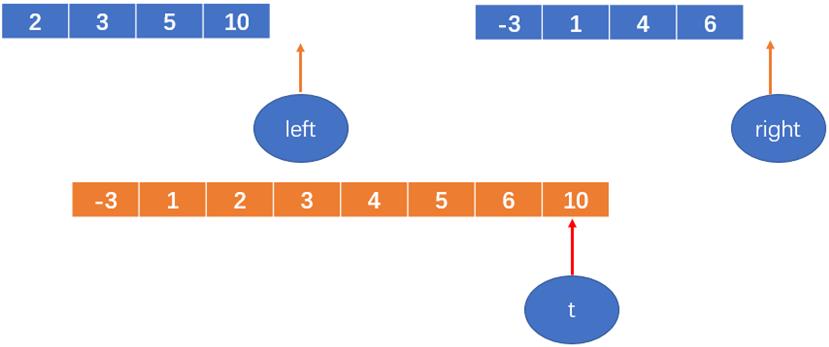
       …以此类推，直到子数组中的数都填过来；

代码实现

/*
 合并方法：
   @param arr 待排序数组
   @param left 左边序列的初始索引
   @param mid 中间索引(用来判断左边序列何时结束：到mid结束,右边序列何时开始：即mid+1)
   @param right 右边数组结束的索引
   @param temp 临时存储的数组
*/

function merge(arr, left, mid, right, temp) 
    var i = left;     //左边有序序列的初始化索引
    var j = mid+1;    //右边有序序列的初始化索引
    var t = 0;        //指向临时数组的当前索引
    // 将两边数组元素进行比较，一次填进临时数组，直到将一边填完
    while (i <= mid && j <= right) 
        if (arr[i] <= arr[j]) 
            temp[t] = arr[i];     //将较小的元素添加进去
            t += 1;
            i += 1;
         else 
            temp[t] = arr[j];
            t += 1;
            j += 1;
        
    
    // 将有剩余数据的数组全部填充到数组
    while (i <= mid)       //左边序列有剩余
        temp[t] = arr[i];
        t += 1;
        i += 1;
    
    while (j <= right) 
        temp[t] = arr[j];
        t += 1;
        j += 1;
    
    // 将temp数组的元素拷贝到arr
    t = 0;
    var k = left;
    while (k <= right) 
        arr[k] = temp[t];
        t += 1;
        k += 1;
    

// 归并（分+治）方法
function mergeSort(arr, left, right, temp) 
    if (left < right) 
        var mid = parseInt((left + right) / 2);      //中间索引
        mergeSort(arr, left, mid, temp);             //左边递归分解
        mergeSort(arr, mid+1,right, temp);           //右边递归分解
        merge(arr, left, mid, right, temp);               //合并
    
    

var arr = [2,5,3,10,-3,1,6,4];
var temp = new Array(arr.length);
console.log("排序前的数组：",arr);
mergeSort(arr,0,arr.length-1,temp); 
console.log("排序后的数组：",arr);

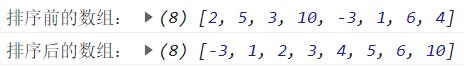
分析

空间复杂度分析

       在将两个数组合并成一个数组的过程中，需要借助额外的存储空间，不难看出，我们将细化到每一个元素的时候，都需要申请一个临时数组来存放数组，比如上面一共对8个元素进行排序，一共执行merge方法7次，所以存储Jon关键随着数据规模的增长而增长，但是在递归的时间，还占用了O(logn)的栈空间，所以总的空间复杂度就是 O(n + logn)，因为量级的原因，所以最终的空间复杂度就是O(n)

是否是稳定的排序算法

       在交换元素时，可以限定元素相等时不移动，所以归并排序是可以稳定的。
       即主要取决于交换元素的时候是否会进行相同元素位置的互换，所以我们会看到merge方法，发现并不会进行元素的互换，但是有个问题，因为在处理剩余元素的时候，采用了es6的扩展运算符，这样会导致相同元素会被直接覆盖，所以如果排序期间有相同元素的情况，还是规矩地写一个while循环来处理

时间复杂度分析

       归并排序的是按照分层进行比较的，会分成log2n层，而每一层的比较次数为O(n)；
       所以时间复杂度求得O(nlogn)。