推荐算法之隐语义模型(LFM)矩阵分解梯度下降算法实现

Posted 2022-01-03 nuist__NJUPT

推荐算法之隐语义模型(LFM)矩阵分解梯度下降算法实现

基于协同过滤的推荐一般分为基于近邻的推荐和基于模型的推荐，其中，基于近邻是指预测时直接使用用户已有的偏好数据，通过近邻数据来预测新物品的偏好。而基于模型的方法，是使用已知偏好数据来训练模型，找到内在规律，再用模型来做预测，类似于回归。

基于模型的方法，在训练时，可以基于标签内容来提取物品特征，可以让模型去发掘物品的潜在特征，这样的模型被称为隐语义模型(LFM)。

用隐语义模型进行协同过滤的目标：揭示隐藏的特征，这些特征解释为什么能给出预测的评分，这类特征可能无法直接用语言描述，但是我们知道有隐藏规律就可以。

协同过滤算法非常依赖历史数据，而一般的推荐系统中，偏好数据往往又是稀疏的，这就需要对原始数据做降维处理。一个大矩阵分解成两个矩阵相乘，分解之后的矩阵就代表用户和物品的潜在特征。

LFM降维方法：矩阵因子分解
假设用户的评分矩阵为R，现有m个用户，n个物品，我们要发现k个隐类，找到两个矩阵P和Q，使得两个矩阵的乘积近似等于R，即用户对物品的评分矩阵分解成了两个低维矩阵。
如下图所示，用户特征矩阵P的每一列都是用户的一个特征向量，电影特征矩阵Q的每一列都是物品的一个特征向量。

一个M×N的打分矩阵可以用两个矩阵P和Q的乘积来近似。

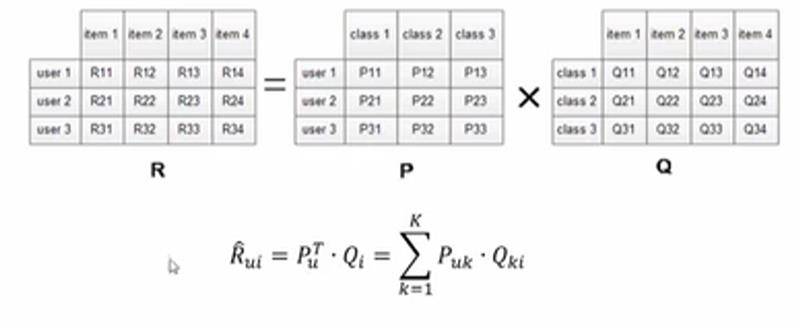
得到P和Q的乘积不再稀疏，之前的矩阵R也可以也可以由P和Q算出，这就得到了一个预测频分矩阵。

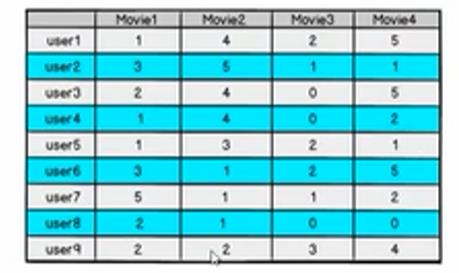
如果得到的预测评分矩阵于原来的评分矩阵在已知的评分位置上都近似，我们就可以认为预测位置上的值也是近似的。

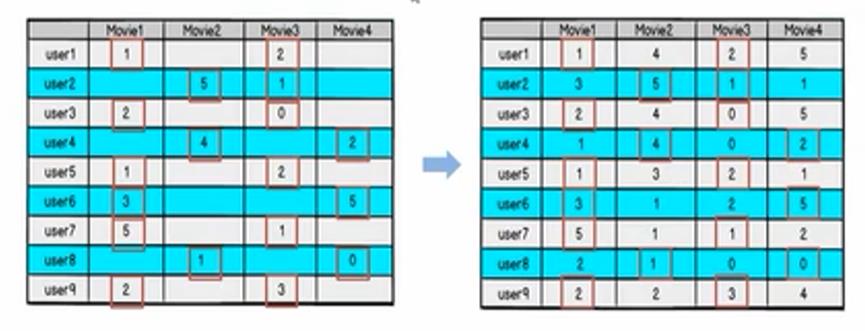
模型的求解
现在得问题是怎样得到这样得分解方式P*Q呢，矩阵分解得到得预测矩阵与原评分矩阵在已知得评分项上可能有误差，我们得目标是找到一个最好得分解方式，让分解之后得预测评分矩阵总误差最小。

我们选取平方损失函数，并加入正则化项，防止过拟合

现在矩阵因子分解问题已经转换成了一个 标准得优化问题，需要求解P和Q使得目标损失函数取得最小值。

最小化求解得过程一般采用随机梯度下降法或者交替最小二乘法来实现。

交替最小二乘法(ALS):ALS得思想是由于两个矩阵P和Q都是未知，且通过矩阵乘法耦合到一起，为了使他们解耦 ，可以先固定Q，把P当作变量，通过损失函数最小化求出P，再反过来，固定P，把Q当作变量，求解处Q，如此交替执行，直到误差满足阈值条件或者达到迭代上限。

ALS具体求解过程：
以固定Q，求解P为例，由于每个用户u都是相互独立的，当Q固定的时候，用户特征向量Pu取得的值与其它用户特征向量无关，所以每个Pu都可以单独求解。

如下图所示，可以将u提出来，转换成一个等价的表达式。

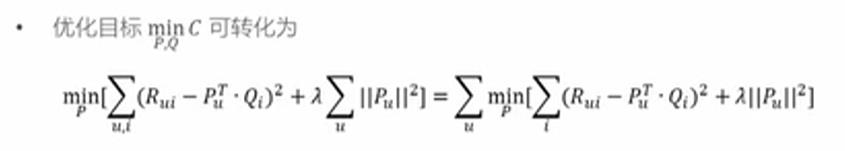
那么令Lu(Pu)如下图所示，我们求其最小值即可。

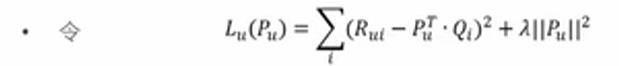
我们对Pu求偏导，并令结果等于0，可得到如下表达式。

最终的化简过程如下所示：

我们主要还是学习用梯度下降的方法去求解隐语义模型。
梯度下降法也是损失函数求偏导，然后将偏导值乘以步长，带入梯度下降公式做迭代就可以。

#引入依赖
import numpy as np
import pandas as pd

#数据准备
#评分矩阵R
R = np.array([[4, 0, 2, 0, 1],
             [0, 2, 3, 0, 0],
             [1, 0, 2, 4, 0],
              [5, 0, 0, 3, 1],
             [0, 0, 1, 5, 1],
             [0, 3, 2, 4, 1]])
'''
输入参数：
R：M×N的评分矩阵
K：隐特征向量的维度
max_iter:最大迭代次数
alpha:步长
lamda:正则化系数

输出：
分解之后的P,Q
P:用户特征矩阵M*K
Q：物品特征矩阵N*K

'''

#给定超参数
K = 5 #维度设为5
max_iter =  5000
alpha = 0.0002
lamda = 0.004

#核心算法
def lfm_grad_desc( R, max_iter,  lamda,  K, alpha):
    #基本维度参数定义
    M = len(R)
    N = len(R[0])
    #P与Q的初始值
    P = np.random.rand(M,K)
    Q = np.random.rand(N,K)
    Q = Q.T #Q矩阵的转置

    #开始迭代
    for step in range(max_iter):
        #对所有的用户u和物品i遍历,对应的特征向量Pu和Qi梯度下降
        for u in range(M):
            for i in range(N):
                #对于有评分的，求出预测评分误差
                if R[u][i] > 0:
                    eui = np.dot(P[u,:], Q[:,i]) - R[u][i] #评分误差
                    #带入公式，带入梯度下降算法更新当前的Pu和Qi
                    for k in range(K):
                     P[u][k] = P[u][k] - alpha  * (2 * eui * Q[k][i] + 2 * lamda * P[u][k])
                     Q[k][i] = Q[k][i] - alpha  * (2 * eui * P[u][k] + 2 * lamda * Q[k][i])
        #u,i遍历完成，所有特征向量更新完成，可以得到P，Q，可以计算预测评分矩阵
        predR = np.dot(P, Q)

        #计算当前损失函数
        cost = 0
        for u in range(M):
            for i in range(N):
                if R[u][i] > 0:
                    cost += (np.dot(P[u,:], Q[:,i]) - R[u][i]) ** 2
                    #加上正则化项
                    for k in range(K):
                        cost += lamda * (P[u][k] ** 2 + Q[k][i] ** 2)
        if cost < 0.0001:
         break
    return P ,  Q.T, cost



P, Q, cost = lfm_grad_desc(R, max_iter,  lamda,  K, alpha)
print(P)
print(Q)
print(cost)
print(R)
predR = P.dot(Q.T)
print(predR)

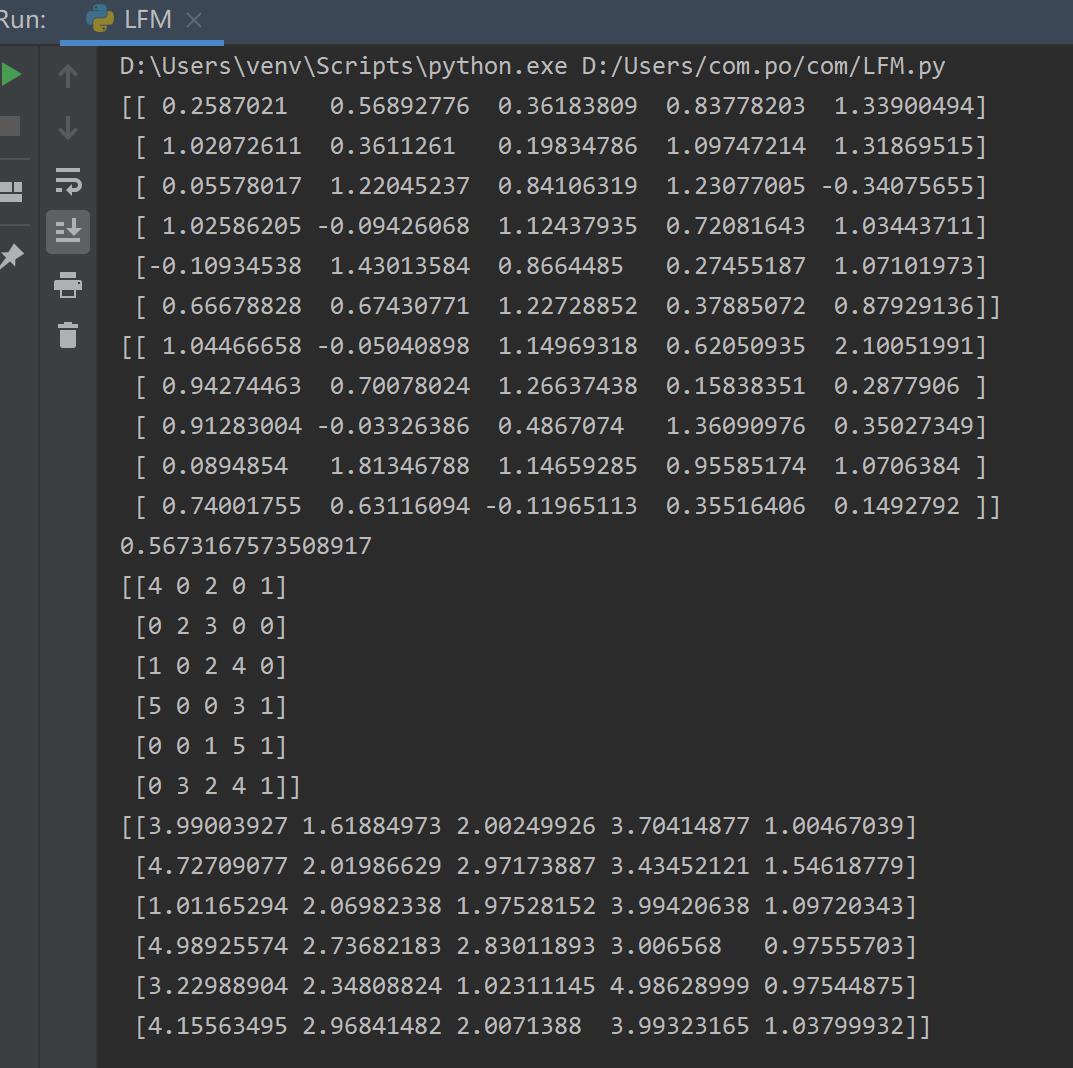
我们观察一下输出结果：
矩阵P为6行5列，矩阵Q为6行5列，列数5为维度
损失函数为0.567
最后两个矩阵为稀疏的原始评分矩阵和饱满的预测评分矩阵。