十大经典排序之：基数排序 ｜计数排序

Posted 2021-12-28 菜菜bu菜

十大经典排序之：归并排序 ｜桶排序

• 基数排序
• • 基数排序原理
  • 算法实现
  • 例题
• 计数排序
• • 计数排序原理
  • 算法实现
  • 例题

基数排序

基数排序原理

今天的排序算法可能比之前的稍微难点。基数排序是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。属于“分配式排序”（distribution sort），又称“桶子法”（bucket sort）或bin sort。最早用于解决卡片排序的问题。

基数排序是可以应对字符的，针对于字符串的基数排序就诞生了，它是在计数排序的基础上进行了改进，在某些时候，基数排序法的效率高于其它的稳定性排序法。基数排序从最低为开始来排序的，从低位到高位，按位排序，按位排序必须是稳定的。

基本思想：对于每个元素x，如果我们知道了小于x的元素的个数，就可以确定输出数组中元素x的位置，那么直接将元素x放到输出数组中。比如有3小于x的元素，那在输出数组中，x肯定位于第4个位置。

算法实现

1、算法描述

1. 将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零。
2. 从最低位开始，依次进行一次排序。
3. 这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。

2、图示

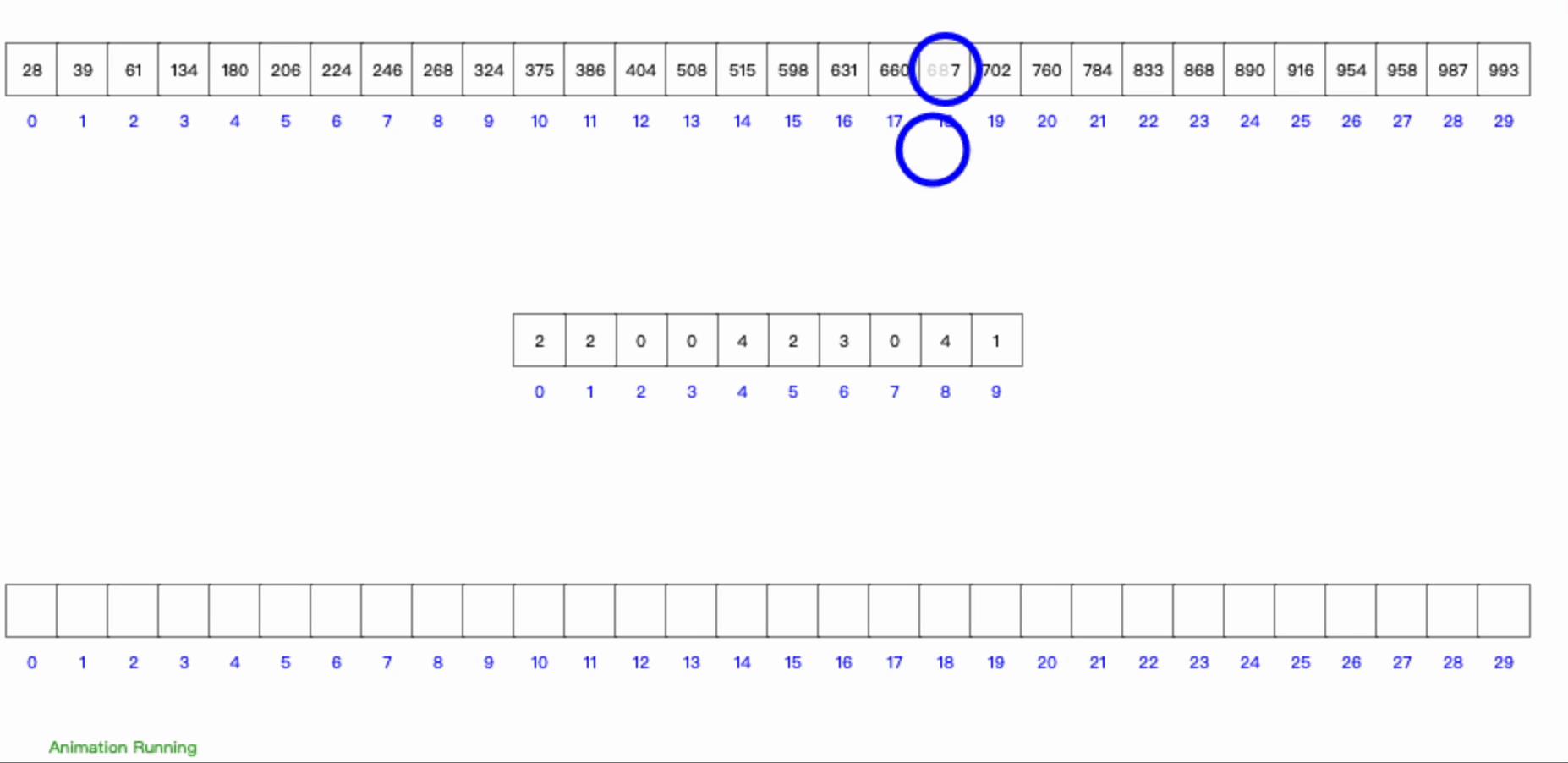
3、算法空间复杂度和时间复杂度
时间复杂度：

• 最坏：o（$d（r+n）$）
• 最好：o（$d（rd+n）$）
• 平均：o（$d（r+n）$）

空间复杂度（辅助存储）：o（rd+n）
稳定性：稳定

ps：r：关键字基数 d：长度 n：关键字个数

例题

用基数排序将以下数列按照从小到大的顺序输出：123,45,6,22,99,1,38,41,7,0

java代码：

import java.util.*;
public class Test 
    //pos=1表示个位，pos=2表示十位
    public static int getNumInPos(int num, int pos) 
        int tmp = 1;
        for (int i = 0; i < pos - 1; i++) 
            tmp *= 10;
        
        return (num / tmp) % 10;
    
    
    //求得最大位数d
    public static int getMaxW(int[] arr) 
        int max = arr[0];
        for (int i = 0; i < arr.length; i++) 
            if (arr[i] > max)
                max = arr[i];
        
        int tmp = 1, d = 1;
        while (true) 
            tmp *= 10;
            if (max / tmp != 0) 
                d++;
             else
                break;
        
        return d;
    
    public static void radixSort(int[] arr, int d) 
        int[][] array = new int[10][arr.length + 1];
        for (int i = 0; i < 10; i++) 
            array[i][0] = 0;
            // array[i][0]记录第i行数据的个数
        
        for (int pos = 1; pos <= d; pos++) 
            for (int i = 0; i < arr.length; i++) 
                // 分配过程
                int row = getNumInPos(arr[i], pos);
                int col = ++array[row][0];
                array[row][col] = arr[i];
            
            for (int row = 0, i = 0; row < 10; row++) 
                // 收集过程
                for (int col = 1; col <= array[row][0]; col++) 
                    arr[i++] = array[row][col];
                
                array[row][0] = 0;
                // 复位，下一个pos时还需使用
            
        
    

    public static void main(String[] args) 
        int[] arr=new int[]123,45,6,22,99,1,38,41,7,0;
        //基数排序
        radixSort(arr,getMaxW(arr));

        System.out.println("基数排序后的结果是:");
        System.out.println(Arrays.toString(arr));
    

计数排序

计数排序原理

计数排序是一个非基于比较的排序算法，它的优势在于在对一定范围内的整数排序时，快于任何比较排序算法。其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中，作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

简单来说，就是通过数组下标来确定正确的位置，并在数组中记录出现的次数，最后得到有序数据。

核心思想：统计每个整数在序列中出现的次数，进而推导出每个整数在有序序列中的索引

算法实现

1、算法描述

1. 找出待排序的数组中最大和最小的元素
2. 统计数组中每个值为i的元素出现的次数，存入数组C 的第i项
3. 对所有的计数累加 (从C 中的第一个元素开始，每一项和前一项相加）
4. 反向填充目标数组：将每个元素i放在新数组的第C[i]项，每放一个元素就将C[i]减去1

2、图示

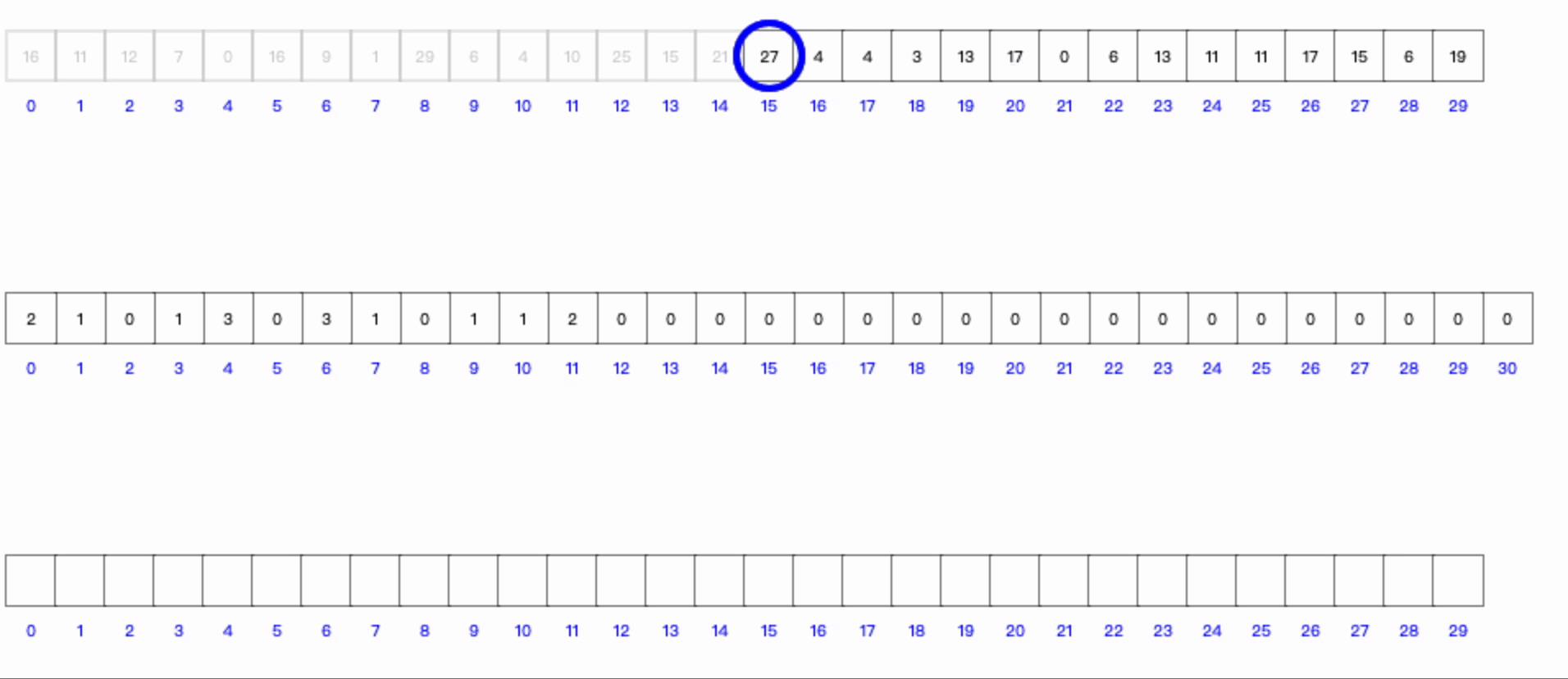
3、算法空间复杂度和时间复杂度
时间复杂度：

• 最坏：o（$n+k$）
• 最好：o（$n+k$）
• 平均：o（$n+k$）

空间复杂度（辅助存储）：o（$n+k$）

稳定性：稳定

例题

用计数排序将以下数列按照从小到大的顺序输出：
66,13,51,76,81,26,57,69,23

java代码：

import java.util.*;
public class Test 
    public static void countSort(int[] arr) 
        int min = arr[0];
        int max = arr[0];

        for (int i = 1; i < arr.length; i++) 
            if (min > arr[i])  min = arr[i];
            if (max < arr[i]) max = arr[i];
        
        // 构建一个新的数组，把原数组中数据的值当作下标存入，下标从0开始；因为max要放入对应下标中，所以要+1
        int[] bucketArr = new int[max + 1];
        for (int k = 0; k < arr.length; k++) 
            //数字每出现一次，就在原基础上+1
            bucketArr[arr[k]] = bucketArr[arr[k]] + 1;
        
        
        int finalIndex = 0;
        for (int n = min; n < bucketArr.length; n++) 

            if (bucketArr[n] > 0) 
                for (int l = 0; l < bucketArr[n]; l++) 
                    arr[finalIndex++] = n;
                
            
        
    


    public static void main(String[] args) 
        int[] arr=new int[]66,13,51,76,81,26,57,69,23;
        //记数排序
        countSort(arr);

        System.out.println("记数排序后的结果是:");
        System.out.println(Arrays.toString(arr));