吴恩达深度学习笔记
Posted 好奇小圈
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了吴恩达深度学习笔记相关的知识,希望对你有一定的参考价值。
神经网络
文章目录
前言
学习的第二天
一、一些基础的numpy语法
import numpy as np
a=np.array([1,2,3,4])#生成数组
print(a)
import time
a=np.random.rand(1000000)#生成随机数
b=np.random.rand(1000000)
tic=time.time()#计时
c=np.dot(a,b)#点乘
toc=time.time()
print("array time is:"+str(1000*(toc-tic))+"ms")#输出+类似js的字符串合并+强制类型转换
c=0
tic=time.time()#计时
for i in range(1000000):#循环
c+=a[i]*b[i]
toc=time.time()
print("loop time is:"+str(1000*(toc-tic))+"ms")
n=4
u=np.zeros((n,1))#生成零数组
for i in rang n:
u[i]=math.exp(a[i])#指数函数
'''
np.log(v)
np.abs(v)
np.sum(v)
np.maxnum(v,0)找包括零的所有数中的最大数
v**2是每个数的平方
1/v就是倒数
'''
import numpy as np
a=np.array([[56,0,4.4,68],[1.2,104,52,8],[1.8,135,99,0.9]])#二维数组
print(a)
b=np.sum(a,axis=0)#列项求和
#也可以b=a.sum(axis=0)
c=100*a/b.reshape(1,4)#a点除b,reshape:让数组变成1行4列
print(c)
#assert(断言)用于判断一个表达式,在表达式条件为 false 的时候触发异常。
同时,python中初始化向量时应注明行列,否则会出现无法转置的奇怪问题。如果你不确定中间结果是不是符合预期,可以使用
assert(a.shape==(5,1))
进行判断,然后用reshape重塑
a=a.reshape((5,1))

上一节提到的logistics损失函数,主要是基于伯努利分布和极大似然的原理
二、神经网络
1、原理
已经有模式识别和数学建模基础,故此处简写

具有logistics相似的反向传播,虽然有三层,但一般称作双层神经网络,因为一般输入层不算上。

向量化:



2、代码
我这里用MATLAB实现了一个双层的
MATLAB版本:
clc;clear;
m=10;n=5;
x=[1:5]';
x=[x*ones(1,5),x*ones(1,5)*0.1];
x=x+0.2*rand(n,m)-0.1;
y=[1,1,1,1,1,0,0,0,0,0];%生成原始标签
%初始化
%第一层
node=20;%你想要的节点数量
w1=0.1*ones(node,5);%初始权重w1
b1=0.1*ones(node,1);%初始化b1
z1=rand(20,10);
%第二层
w2=ones(1,node);
b2=1;
z2=w2*z1+b2;
a=0.01;%学习率
N=1000;
z2=zeros(1,m);
dz2=zeros(1,m);
%已知训练集x(n*m),标签Y(m*1),以及初始的w(1*n),b(1*1),训练次数N,学习率a
%先反向传播第二层
for i=1:N
z2=w2*z1+b2;
A2=1./(1+exp(-z2));
dz2=A2-y;
dw2=1/m*z1*dz2';
db2=1/m*sum(dz2);
w2=w2-a*dw2';
b2=b2-a*db2;
end
%后反向传播第一层
N=1000;
Y=z1;
dz1=zeros(size(z1));
%已知训练集x(n*m),标签Y(m*1),以及初始的w(1*n),b(1*1),训练次数n,学习率a
for i=1:N
z1=w1*x+b1;
A1=1./(1+exp(-z1));
dz1=A1-Y;
dw1=1/m*x*dz1';
db1=1/m*sum(dz1);
w1=w1-a*dw1';
b1=b1-a*db1;
end
Z1=w1*x+b1;
Z2=w2*Z1+b2;
A=1./(1+exp(-Z2));
AA=A;
A(find(A>=0.5))=1;
A(find(A<0.5))=0;
percent=sum(sign(find(A==y)))/10
J=-1/10*sum(y.*log(AA)+(1-y).*log(1-AA))
还有
python版本:
import numpy as np
m=10
n=5
x=np.array([1,2,3,4,5])
x=x.reshape(n,1)
x1=x*np.ones((1,n))+0.5*np.random.randn(n,n)
x2=0.1*x*np.ones((1,n))+0.05*np.random.randn(n,n)
x=np.concatenate((x1,x2),axis=1)
y=np.array([[1,1,1,1,1,0,0,0,0,0]])#生成原始标签
#初始化
#第一层
node=20#你想要的节点数量
w1=0.1*np.ones((node,5))#初始权重w1
b1=0.1*np.ones((node,1))#初始化b1
z1=np.random.rand(20,10)
#第二层
w2=np.ones((1,node))
b2=1
z2=w2@z1+b2#python的矩阵乘法还挺麻烦
a=0.01#学习率
N=1000
z2=np.zeros((1,m))
dz2=np.zeros((1,m))
#先反向传播第二层
for i in range(N):
z2=w2@z1+b2
A2=1/(1+np.exp(-z2))
dz2=A2-y
dw2=1/m*z1@dz2.swapaxes(0,1)#转置
db2=1/m*dz2.sum()
w2=w2-a*dw2.swapaxes(0,1)
b2=b2-a*db2
Y=z1
dz1=np.zeros(np.size(z1))
#已知训练集x(n*m),标签Y(m*1),以及初始的w(1*n),b(1*1),训练次数n,学习率a
for i in range(N):
z1=w1@x+b1
A1=1/(1+np.exp(-z1))
dz1=A1-Y
dw1=1/m*x@dz1.swapaxes(0,1)
db1=1/m*sum(dz1)
w1=w1-a*dw1.swapaxes(0,1)
b1=b1-a*db1
Z1=w1@x+b1
Z2=w2@Z1+b2
A=1/(1+np.exp(-Z2))
temp=0
AA=np.array(A)#numpy.array的数组只能这么复制,否则复制的是指针
for i in range(10):
if A[0,i]>=0.5:
A[0,i]=1
else:
A[0,i]=0
if A[0,i]==y[0,i]:
temp+=1
percent=temp*10
print("正确率为"+str(percent)+"%")#必须强制类型转换
J=-1/10*np.sum(np.dot(y,np.log(AA).T)+np.dot(1-y,np.log(1-AA).T))
print("损失函数数值为"+str(J))
正确率为100%
损失函数数值为0.43208082228886674
由于二分类问题比较简单,因此正确率还是不错的,学过MATLAB,没学python,但numpy库很多只是比MATLAB多了个numpy.······但是会遇到上面提到的奇奇怪怪的bug,人性化程度不如MATLAB
3、激活函数
tanh函数
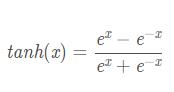

Relu函数


其原点无意义
Leaky ReLU函数(PReLU)


ELU (Exponential Linear Units) 函数


初值应尽量小
总结
以上是关于吴恩达深度学习笔记的主要内容,如果未能解决你的问题,请参考以下文章