一文彻底解析数据库设计思路

Posted 苏州程序大白

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了一文彻底解析数据库设计思路相关的知识，希望对你有一定的参考价值。

一文彻底解析数据库设计思路

目录

🌟博主介绍

💂 个人主页:苏州程序大白

💂 个人社区:CSDN全国各地程序猿

🤟作者介绍：中国DBA联盟(ACDU)成员，CSDN全国各地程序猿（媛）聚集地管理员。目前从事工业自动化软件开发工作。擅长C#、Java、机器视觉、底层算法等语言。2019年成立柒月软件工作室。

💬如果文章对你有帮助，欢迎关注、点赞、收藏（一键三连）和C#、Halcon、python+opencv、VUE、各大公司面试等一些订阅专栏哦

🎗️ 承接各种软件开发项目

💅 有任何问题欢迎私信，看到会及时回复

👤 微信号：stbsl6，微信公众号：苏州程序大白

🎯 想加入技术交流群的可以加我好友，群里会分享学习资料

实体关系(Entity-Relationship, E-R)概念

  • E-R 模型是一种描述数据库的抽象方法。

  • 实体关系建模的方法更多依赖于直觉而非机器, 但会导致相同的设计。

E-R 模型

实体 (Entity)

实体是具有公共性质的可区别的现实世界对象集合。

举例：

  • 学生

  • 教师

  • 课程

  • 选课

一般而言, 一个实体被映射到一张关系表中, 代表一组对象的集合; 表中的每一行被称为一个实体发生(Entity Occurrence)或实体实例(Entity Instance), 代表一个特定对象。

在 E-R 图中, 用矩形框表示：

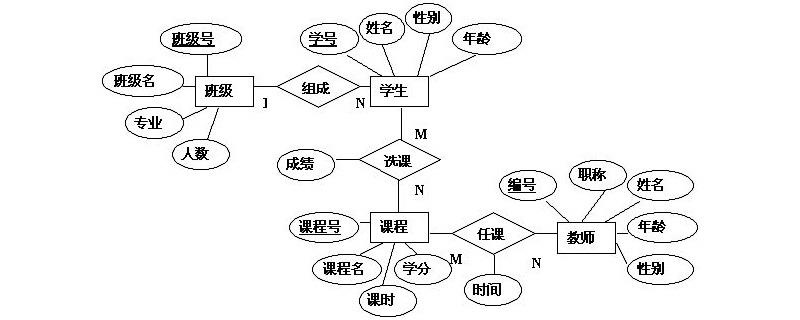
属性 (Attribute)

属性是描述实体(Entity)或者关系(Relationship)性质的关系项。

在 E-R 图中, 用椭圆框表示, 主标识符要加下划线, 多值属性要加一条线。

特定属性的特定术语：

  • 标识符或候选键 (Identifier 或 Candidate Key)
    标识符是能够唯一识别一个实体实例的属性集, 一个实体可以有多个标识符。

  • 主键或主标识符 (Primary Key)
    被数据库设计者选择出来的作为表中特定行唯一标识符的候选键, 一个实体只有一个主标识符。

  • 描述符(Descriptor)
    描述性的非键属性, 如年龄。

  • 复合属性
    一组共同描述一个性质的简单属性。

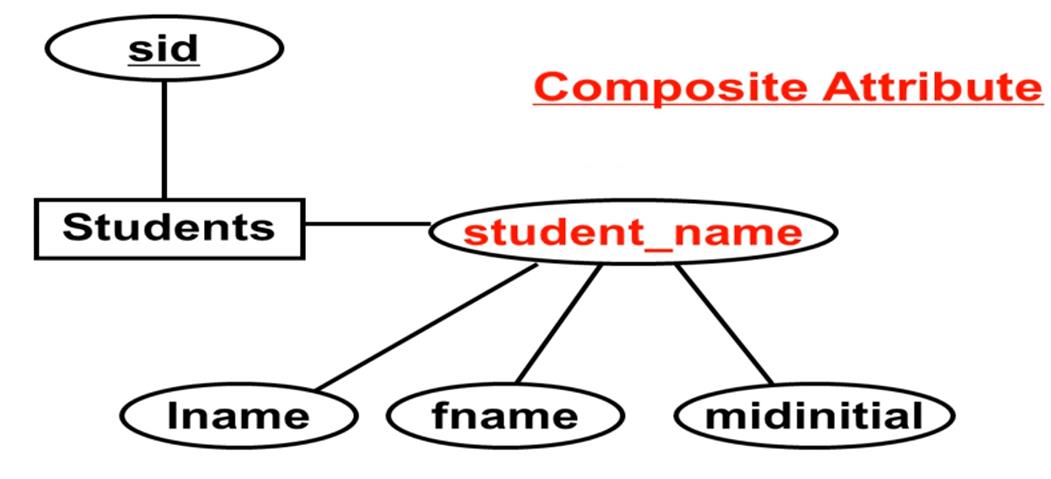
  • 多值属性

单个实例这个属性可以具有多个值, 如下图: 一个人可以有多个爱好

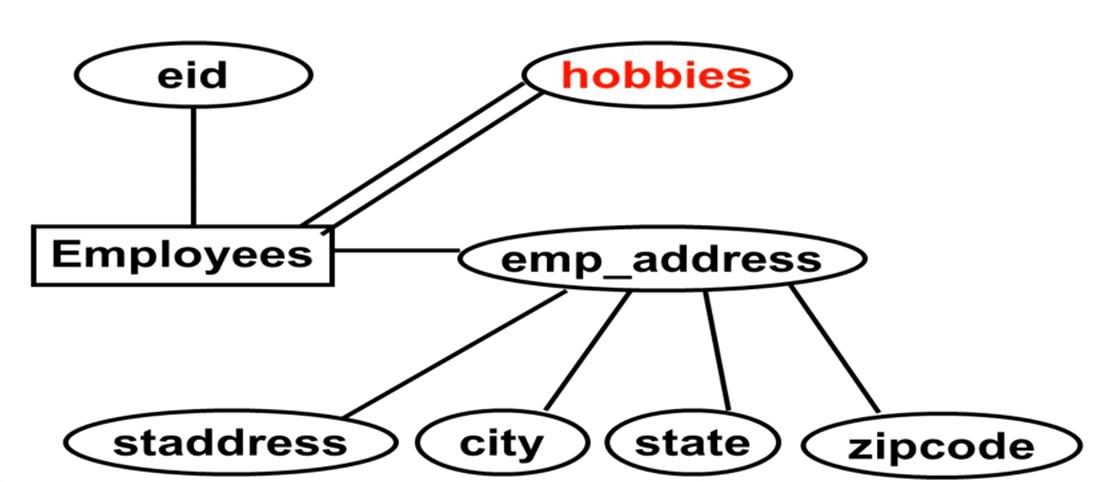
联系(Relationships)

  • 给定一个包含 m 个实体的有序列表, E1, E2,…, Em(一个实体可以出现多次)。

  • 一个联系 R 当以了这些实体实例之间的对应规则。

  • 特别地 R 代表了一个 m 元组的集合, 它是笛卡尔积 E1× E2× …× Em的子集。

  • 联系用菱形表示, 联系也能附加属性。

举例:

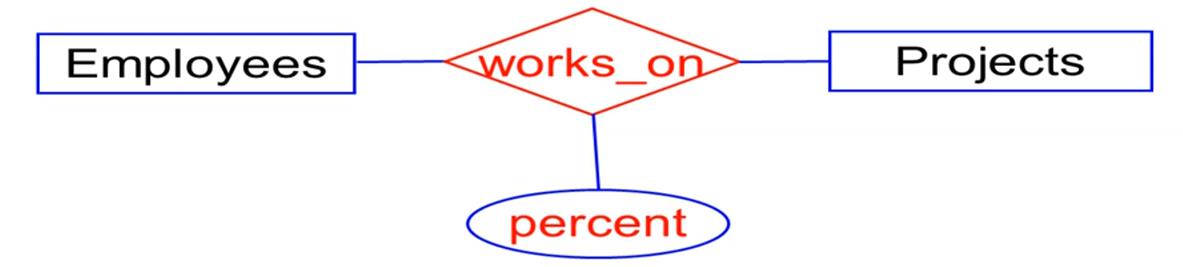
将实体和属性转换为关系

规则一

  • 一个实体映射到关系型数据库中的一张表. 实体的单值属性被映射为表的列(复合属性被映射为多个简单列)。

  • 实体标识符映射为候选键。

  • 实体主标识符映射为主键。

  • 实体的实例映射为表中的一行。

举个例子: 按上面出现过的图, Students(sid, Iname, fname, midiaitia)

规则二

  • 多值属性必须被映射成它自己的表。

举例: 对于上面的 hobbies 多值属性, 将 hobbies 单独映射成一张表hobbies(hobby,eid)。

规则三: N-N Relationships

  • 当两个实体 E 和 F 参与一个多对多二元联系 R 时, 在相关的关系型数据库中, 联系被映射成一个表 T, 表 T 中包含所有从 E 和 F 转化而来的两个表的主键的所有属性, 列构成了表 T 的主键。

  • T 也包含了所有附加在联系 R 上的属性构成的列。

简单来讲, 就是 N-N 联系中, 将联系单独转换成一张表, 表的主键是 E 和 F 的表的主键, 还要加上附加的属性

上面这好似读天书一般, 举个例子:


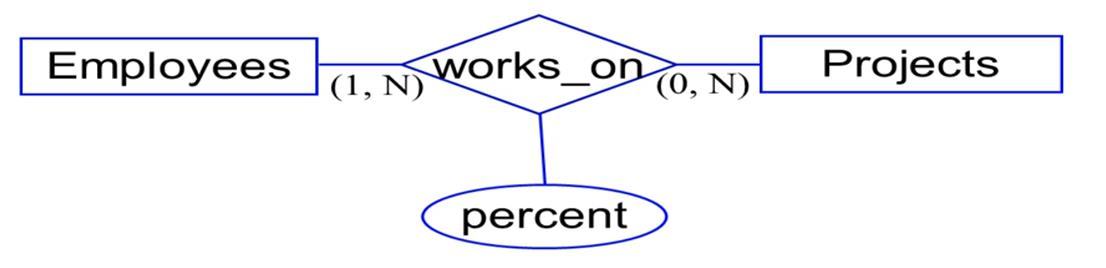
Employees 和 Projects 是 N-N 的关系, 可以得到三张表:

  • Employees(eid, straddr, city,…)

  • Projects(prid, proj_name, cue_date)

  • work_on(eid, prid, percent)

规则四: N-1 Relationships

当两个实体 E, F 参与 N-1 的二元联系 R 时, 这个关系不能被映射成自身的一个表。

若 max_card(F, R) = 1,并且 F 为联系中的多方, 那么从实体 F 转换出的关系表 T 中包括从 E 转换出的关系表的主键属性列, 这被称为 T 的外键(可以简单理解为表的一列是另一张表的主键, 这两张表是有关联的)。

若 F 强制参与, F 转换出的关系表中外键列不允许为空;若 F 是选择参与, 允许为空。

简单来讲, N-1 联系: 两个实体转换成两张表, 为 N 方的表需要包含外键(1 方的主键)，举例:


一个 Instructors 可以对应多个 Course_sections, 一个Course_sections 只能对应一个 Instructors, 所以映射成两张表:

  • Instructors(insid, Iname,…)

  • Course_sections(secid, insid, course,…)

规则五&六: 1-1 Relationships

  • 有一侧是可选参与

  • 若两张表都是可选参与: 选一张表插入另一张表的主键属性列作为外键;

= 若有一张表是强制参与: 在强制参与的实体表中添加外键列(非空的)

  • 都是强制参与

  • 最好将两张表合并, 避免使用外键

E-R 图更多的细节

基数 (Cardinality of Entities Participation in a Relationship)

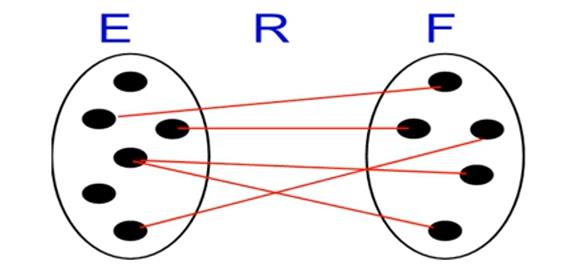
  • 实体 E, F 联系 R。

  • 点表示实体的实例, 先表示联系的实例。

  • max-card 和 min-card。

  • 一个实例出去两条或两条以上的线, max-card = n;一个实例出去零条线, min-card = 0。
    举例:

1个雇员可以管理 0 ~ n个雇员。

1个雇员最多向 1 个雇员报告(最高层管理没有上一级)。

多值参与和单值参与 (single-valued participation and multi-valued participation)

max-card(X, R) = 1, X 单值参与 联系 R

max-card(X, R) = n, X 多值参与 联系 R

强制参与和可选参与 (mandatory participation and optional participation)

min-card(X, R) = 1, X 强制参与 联系 R

max-card(X, R) = 0, X 可选参与 联系 R

One-to-One, Many-to-Many, and Many-to-One Relationship

One-to-One: 两个实体均为单值参与

Many-to-Many: 两个实体均为多值参与

Many-to-One: 一个实体多值参与, 另一个实体单值参与

弱实体 (Weak Entities)

如果一个实体的所有实例都通过联系 R 依赖于另一个实体的实例而存在, 这个实体就是弱实体, 另一个实体是强实体。

举例:


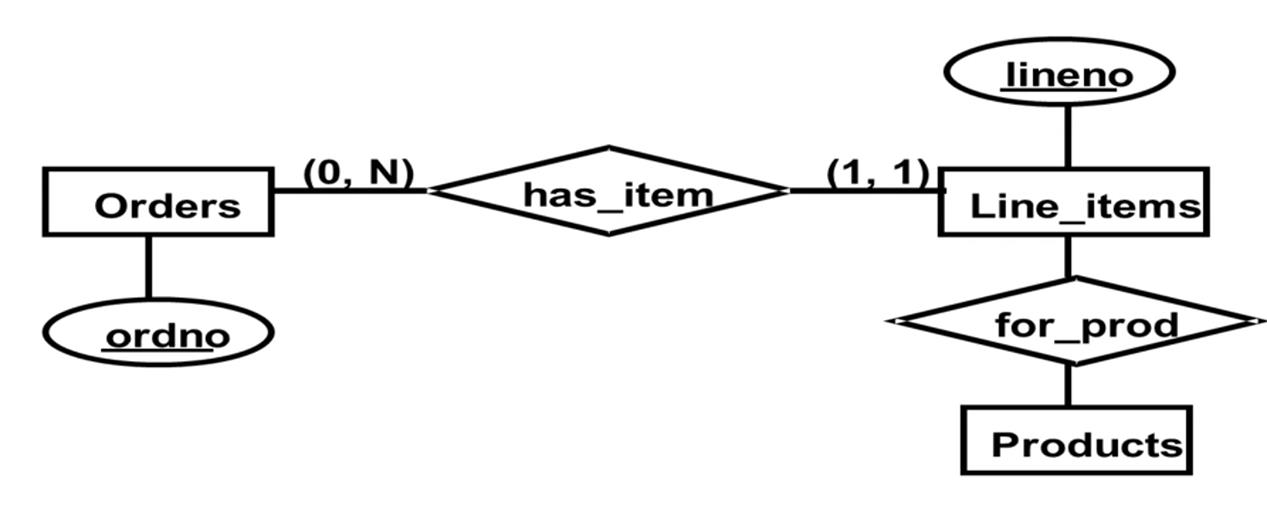
弱实体 Line_items, 强实体 Orders, Line_items 的主标识符 Line_number 只有存在于某个订单中时, 才是有意义的. 若 订单取消了, Line_items 中所有相关的记录也会消失。

若 Line_items 映射为一张关系表, ,按照规则四, Orders 的主键 oid 被加入进来, 表的主键由外属性 Oid 和弱实体标识符 Line_number 组成。

泛化层次

这不就是继承吗

函数依赖 (Functional Dependency, FD)

  • 定义: A->B, 读作 A 决定B (或者 B 依赖于A ), 意为对于 T 中的两行 r1 和 r2, 若r1(A) = r2(A) 则 r1(B) = r2(B)\\

  • 完全函数依赖: X->Y, 对于 X 的任意一个真子集 X’, X’->Y 均不成立, 则称 Y 完全依赖于 X. 如 (学号, 课程)->成绩

  • 部分函数依赖:Y 不完全依赖于 X, 如 (学号, 课程)->姓名, 只用学号就能决定姓名了

举例:

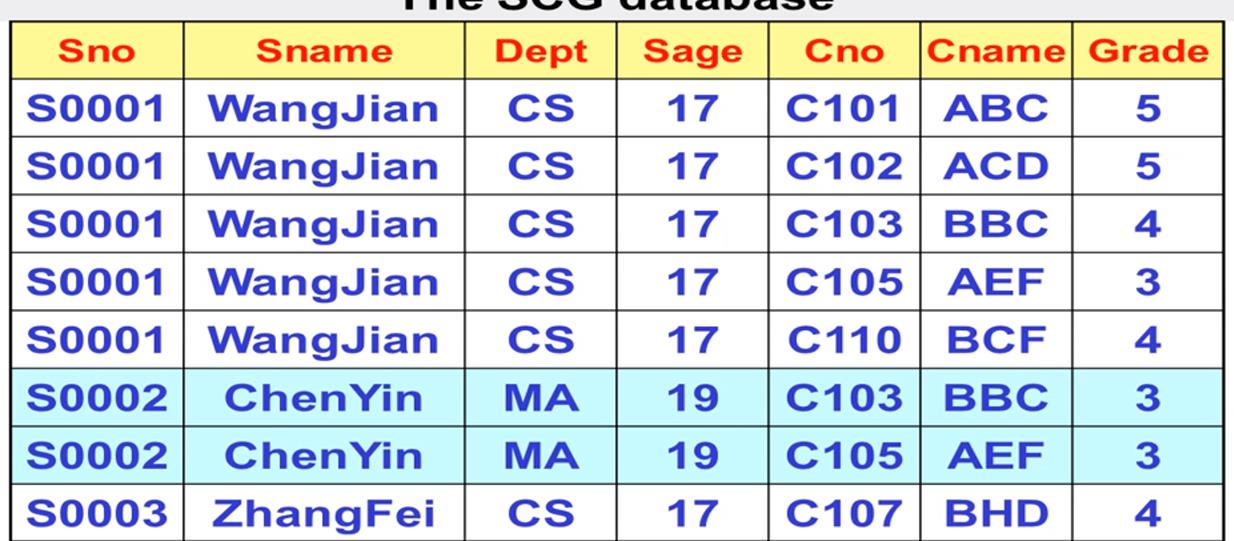
Sno->Sname…

Armstron规则:


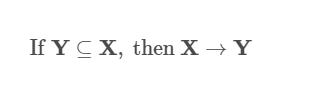
X 都相等了, X 的子集肯定也相等

  • 传递规则:

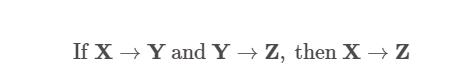
  • 增广规则:

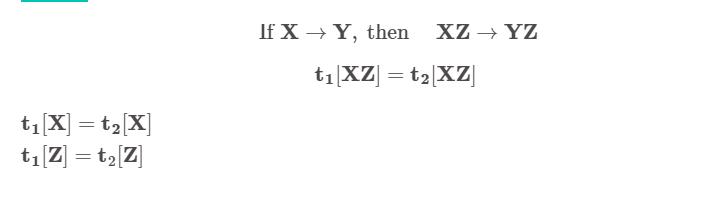
Armstrong 公理的蕴含

合并规则：

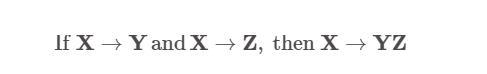
分解规则：

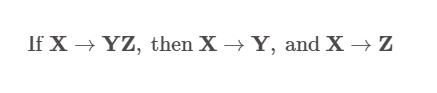
伪传递规则：

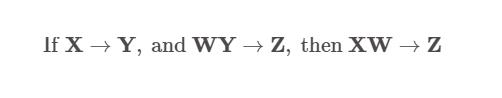
聚积规则：

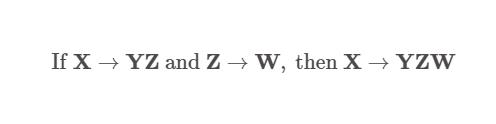
例题:

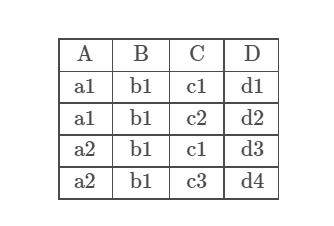
存在的函数依赖: A->B, D->ABC, AC->D C->D, 首先找左边只有一个的, 然后找左边有多个的(排除掉没有被依赖的和决定所有其他的), 如果可以用 Armstrong 公理推出, 就不需要一个一个看。

函数依赖集的闭包(Closure of a Set of FDs)

给定一个函数依赖集 F 作用在表 T 的属性上, 定义 F 的 闭包(记作 F+)为 F 推导出的所有函数依赖的集合

  • F 中有两个函数依赖 a, b, 基于 Armstrong 公理和 a,b 可以得到新的函数依赖 c, c 就是 F 推导出的函数依赖。

  • 如果 d 是平凡依赖 (X->Y 且 Y⊆X), d 是由 F 推导出的函数依赖。

  • F 中的函数依赖都属于 F+。

函数依赖集的覆盖

对于表 T 上的两个函数依赖集 F 和 G, 如果 G 可从 F 由蕴含规则推导出来(即 G ⊆ F+, F 覆盖 G)。

函数依赖集的等价

F 覆盖 G, G 覆盖 F, 则 F 等价于 G

属性集的闭包

给定表 T 的函数依赖集 F 和属性集 X, X 的闭包(记作 X+ )作为由 X 决定的最大属性集合 Y, Y 满足 X->Y 并且 Y 存在于 F+

简单讲的话: 在 F + 中, 对于属性集 X 有 X->A, 所有 A 的集合被称作 X+ (A 也在 F+)

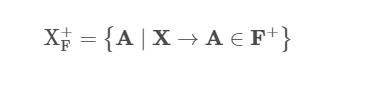
算法:

先把 X+ 赋值为 X, 然后对于函数依赖集 F 中的每一项, 若左侧包含于当前的 X+ , 将右侧的并入 X+, 直到 X+ 中不再增加

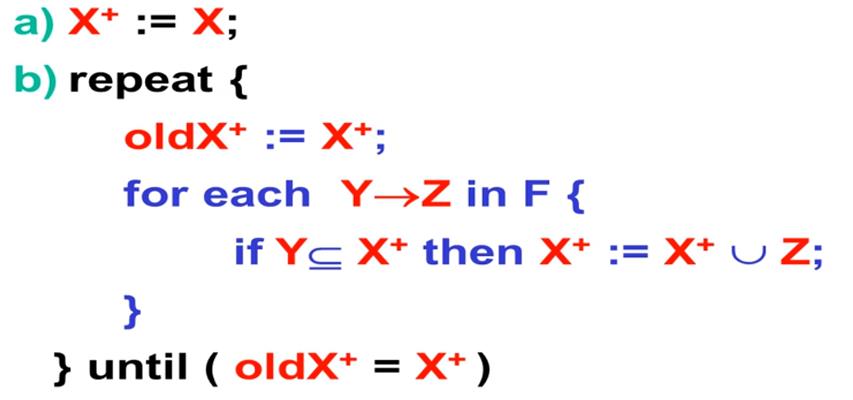
练习:

Example 6.6.7: F=(f1)⁢B→CD,(f2)⁢AD→E , (f3)⁢B→A, compute B+?

答案:

X+ = A,B,C,D,E

最小覆盖

没有冗余的函数依赖

每一个函数依赖的左边都没有多余属性

计算步骤:

1、创建函数依赖集 F 的等价函数依赖集 H, 它的右边只有单个属性

2、顺次去掉 H 中非关键的单个依赖

将 H 中的一项 X->Y 去掉, 得到新的函数依赖集 J, 若 J+ =H + 则称这个函数依赖是非关键的. 
也就是说去除这个函数依赖对 H +没有任何影响。

3、在不改变 H+ 的前提下, 将 H 中的每个函数依赖用左边属性更少的函数依赖替换

注意: 第三部中函数依赖集如果发生了变化, 需要返回第二步

4、用合并规则创建一个等价的函数依赖集 M

来个例题:

F=a→b,b⁢c→d,ac→d, 求 F 的最小覆盖 M

解题步骤:

本来就做好了

依次尝试去掉非关键依赖
尝试去掉 a->b, 得到 G=b⁢c→d,ac→d, aG+ = a, 所以去掉 a->b 后, 在 G 中无法再推导出 a->b, G+ != H+ 不能去掉.尝试去掉 bc->d, 得到 G=a→b,ac→d, b,cG+ = b,c, 不包含 d, 不能去掉尝试去掉 ac->d, G=a→b,b⁢c→d, a,cG+ = a,c,b,d, 包含了 d, 所以去掉后的函数依赖集 G 仍然可以推导出所有的函数依赖, 即 G+ = F+ , 是非关键依赖, 可以去掉。

上一步的结果:

F=a→b,b⁢c→d. 尝试减少左侧的属性，尝试将 bc->d 精简为 c->d, 得到 。G=a→b,c→d, 计算 cF+ = c, 不包含 d 所以不能精简将 bc->d 精简为 b->d, 得到G=a→b,b→d, 计算 bF+ = b, 不包含 d 所以不能精简这个例子不需要合并, 最终结果: F=a→b,b⁢c→d

无损分解

规范化的流程

  • 把一张表分解为一张或者多张更小的表，也就是投影到两个或者多个覆盖全部列的子集并有一些公共列。

  • 但将表重新连接起来的时候, 并不总与原表完全相同可能多出一些原来没有的行举个例子:

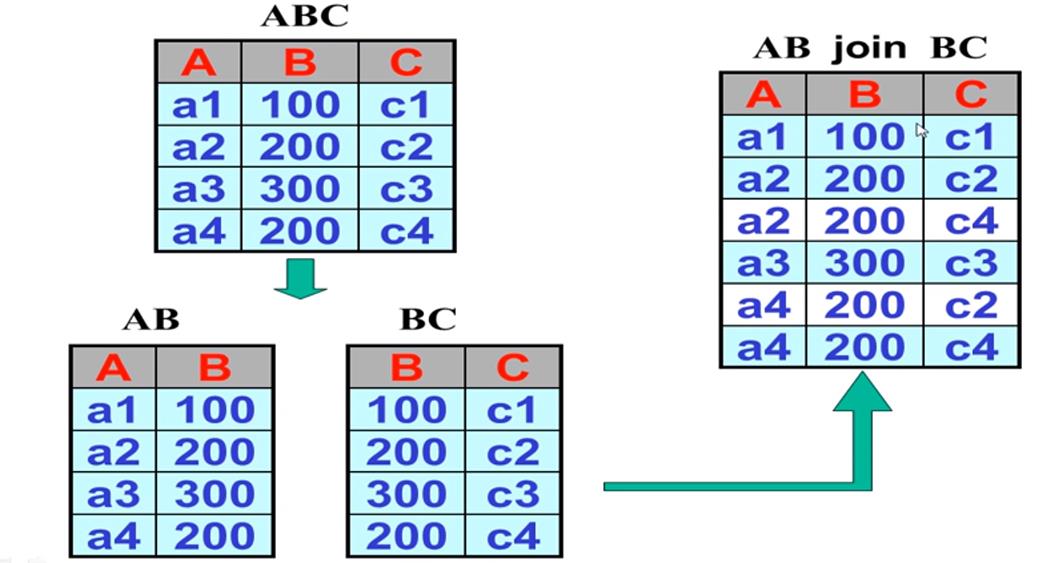
无损 分解

对于一个表 T 和它的一个函数依赖集 F, T 的一个分解(decomposition) 是一个表的集合: T1,T2,…,Tk. 这个集合具有性质:

  • 对于集合中的一个表 Ti , Head(Ti) 是 Head(T) 的一个子集。

  • Head(T) = Head(T1) ∪ Head(T2) ∪….∪…∪ Head(Tk)。

  • 给定表 T 的特定内容, T 的一行被投影到每个 Ti 的列上作为分解的结果 ???。

  • F 中的所有函数依赖需要保证:T≡T1 join T2 join … join Tk。

说人话: 无损分解(也叫无损联接分解) 指将一个关系模式分解为若干个关系模式后, 通过自然连接和投影等运算, 还能回到原来的关系模式. 如果插入了新的记录, 前面的条件仍然必须满足

一个定理

  • 给定一个表 T 和它的一个函数依赖集 F, 一个把 T 分解为 T1,T2的分解是 T 的一个无损分解, 当且仅当 Head(T1) Head(T2 )都是 Head(T) 的真子集, Head(T1)∪ Head(T2 ) = Head(T), 同时以下两个可以由 F 推导出来：

Head(T1) ∩ Head(T2 )-> Head(T1)

Head(T1) ∩ Head(T2 )-> Head(T2).

讲简单点的话: 判断分解成的两个表是不是无损分解, 就得根据表 T 的函数依赖集 F, 检查两张表标题交集能否决定其中一张表的标题

举例子:

F=A→B,T1⁡(A,B),T2⁡(A,C) ,Head(T1) ∩ Head(T2 ) = A, 而 A->AB, 所以是无损分解.

如何无损分解?

每个函数依赖左边的属性在老的核心的表中都出现, 并决定了所有新表中的其他属性

数据库模式 (Database Schema)

  • 一个数据库的模式是数据库所有表的标题的集合, 以及设计者希望在表的连接上成立的所有的函数依赖的集合.

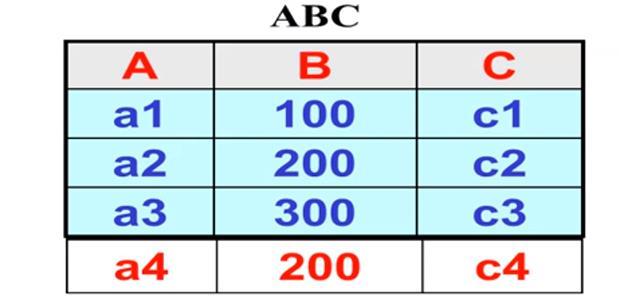
  • 举例子:假定 ABC 有函数依赖 B->C, 则下表是合法的

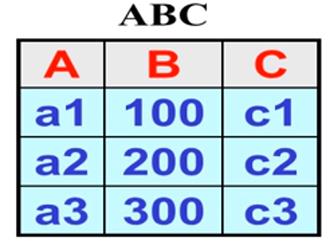
像下面那样插入是非法的, 因为破坏了 B->C

范式 (Normal Form, NF)

设计关系数据库时, 遵从不同的规范要求, 设计出合理的关系型数据库, 这些规范被称为范式目的:

  • 使结构更合理。

  • 消除存储异常。

  • 减小数据冗余。

  • 便于增,删,更新。

保持依赖性 (FD Preserved)

  • 前置条件: 通用表 T, 函数依赖集 F, 无损分解 T1,T2,…,Tk。

  • 对于 F 中的一个函数依赖 X->Y,如果在 Ti 中有 X ∪ Y ⊆Head(Ti), 则称在 Ti 保持了依赖性。

  • 若 F和 (F1∪F2∪…∪Fk) 相互等价, 即 F+=(F1∪F2∪…∪Fk)+ , 称这个分解是保持依赖性的。

超键 (Super Key)

  • 超键在关系中能够唯一标识元组的属性集, 允许有多余属性。

  • 给定表 T 和 它的一组函数依赖集 F, 属性集 X ⊆ Head(T), 下面的描述等价。

  • X 是 T 的超键。

  • X -> Head(T) 或者 X+ F-> Head(T)。

候选键 (Key)

候选键同样可以唯一标识元组, 不允许有多余属性

寻找候选键的算法:


就是依次尝试去掉在 Head(T)中的属性, 若去掉后的属性集在 F 的闭包包含了 T 的所有属性(可以决定 T 所有的属性), 就可以真的去掉了。

主属性 (Primary Attribute)

候选键里的属性就是主属性

范式

1NF

关系型数据库的一张表中, 每一列都不可再分割, 即某一属性不能有多个值

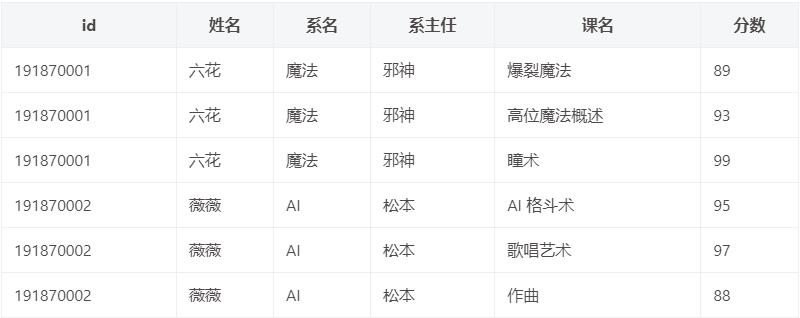
不符合 1NF 的例子:

  • 符合 1NF 的例子:

2NF

课件上的定义何止不是人话, 简直不是人话!

在 1NF 的基础上, 消除了非主属性对于键(指候选键)的部分函数依赖

判断方法:

找出表中所有非主属性
查看是否存在有非主属性对键的部分函数依赖, 若无, 则符合 2NF
修改为符合 2NF:

将数据表拆分成含有较少字段的表
存在的问题: 插入, 删除还是存在异常

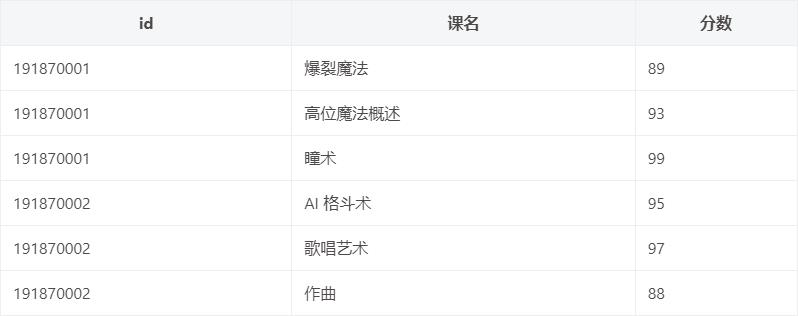
举例: 将之前的表修改为符合 2NF:

候选键:(id,课名),依赖关系: (id, 课名)->分数, id->(姓名,系名,系主任), 可以拆分为两张表


3NF

在 2NF 的基础之上, 消除了非主属性对于键的传递函数依赖. 如果存在非主属性对于键的传递函数依赖, 则不符合 3NF 的要求

传递函数依赖: X->Y, Y->Z, 则 X->Z
修改为符合 3NF:

拆分
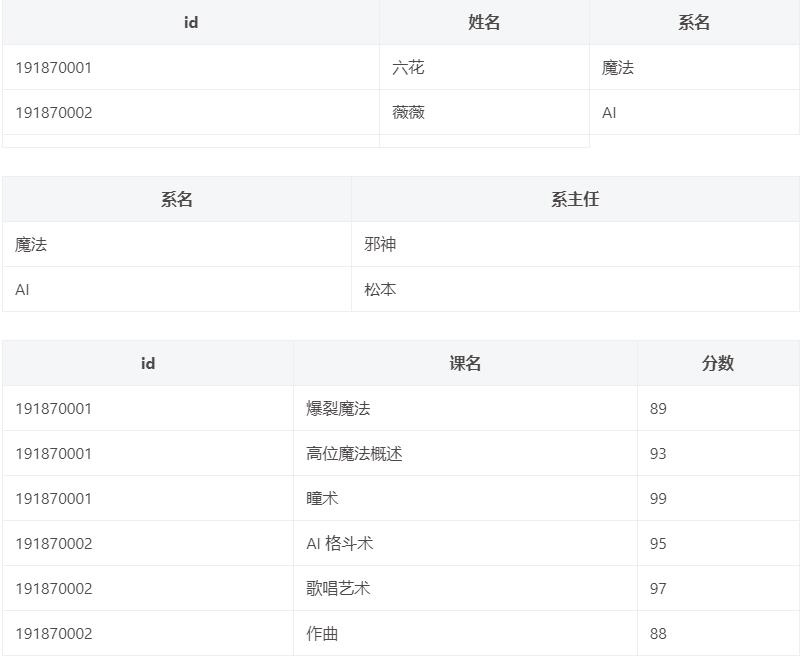
举例

刚才的例子中, 存在 id->系名, 系名->系主任的依赖, 继续将这张表拆分:

BCNF

基于 3NF, 更加严格
在 3NF 基础上消除主属性对候选键的部分依赖和传递依赖
来几个练习题:

R(A,B,C), F=AB->C

候选键: AB, 主属性:A,B,非主属性:C,

C 完全依赖于 AB, 满足 2NF

没有 C 对 AB 的传递依赖, 满足 3NF

满足 BCNF
R(A,B,C), F=B->C,AC->B

候选键: AB, AC, 主属性: A, B, C, 非主属性: 无
最少都会是 3NF
AB 是候选键, B->C , C 作为主属性对 AB 的子集 B 存在依赖, 所以存在主属性对候选键的部分依赖, 不符合 BCNF
R(A,B,C), F=B->C, B->A, A->BC

候选键: A, B, 主属性: A, B, 非主属性: C
满足 3NF
满足 BCNF

🌟作者相关的文章、资源分享🌟

🌟让天下没有学不会的技术🌟

学习C#不再是难问题

🌳《C#入门到高级教程》🌳

有关C#实战项目

👉C#RS232C通讯源码👈

👉C#委托数据传输👈

👉C# Modbus TCP 源代码👈

👉C# 仓库管理系统源码👈

👉C# 欧姆龙通讯Demo👈

👉C#+WPF+SQL目前在某市上线的车管所摄像系统👈

👉2021C#与Halcon视觉通用的框架👈

👉2021年视觉项目中利用C#完成三菱PLC与上位机的通讯👈

👉VP联合开源深度学习编程(WPF)👈

✨有关C#项目欢迎各位查看个人主页✨

🌟机器视觉、深度学习🌟

学习机器视觉、深度学习不再是难问题

🌌《Halcon入门到精通》🌌

🌌《深度学习资料与教程》🌌

有关机器视觉、深度学习实战

👉2021年C#+HALCON视觉软件👈

👉2021年C#+HALCON实现模板匹配👈

👉C#集成Halcon的深度学习软件👈

👉C#集成Halcon的深度学习软件，带[MNIST例子]数据集👈

👉C#支持等比例缩放拖动的halcon WPF开源窗体控件👈

👉2021年Labview联合HALCON👈

👉2021年Labview联合Visionpro👈

👉基于Halcon及VS的动车组制动闸片厚度自动识别模块👈

✨有关机器视觉、深度学习实战欢迎各位查看个人主页✨

🌟Java、数据库教程与项目🌟

学习Java、数据库教程不再是难问题

🍏《JAVA入门到高级教程》🍏

🍏《数据库入门到高级教程》🍏

有关Java、数据库项目实战

👉Java经典怀旧小霸王网页游戏机源码增强版👈

👉js+css类似网页版网易音乐源码👈

👉Java物业管理系统+小程序源码👈

👉JavaWeb家居电子商城👈

👉JAVA酒店客房预定管理系统的设计与实现SQLserver👈

👉JAVA图书管理系统的研究与开发mysql👈

✨有关Java、数据库教程与项目实战欢迎各位查看个人主页✨

🌟分享Python知识讲解、分享🌟

学习Python不再是难问题

🥝《Python知识、项目专栏》🥝

🥝《Python 检测抖音关注账号是否封号程》🥝

🥝《手把手教你Python+Qt5安装与使用》🥝

🥝《用一万字给小白全面讲解python编程基础问答》🥝

🥝《Python 绘制android CPU和内存增长曲线》🥝

🥝《☀️苏州程序大白用万字解析Python网络编程与Web编程☀️《❤️记得收藏❤️》》🥝

有关Python项目实战

👉Python基于Django图书管理系统👈

👉Python管理系统👈

👉2021年9个常用的python爬虫源码👈

👉python二维码生成器👈

✨有关Python教程与项目实战欢迎各位查看个人主页✨

🌟分享各大公司面试题、面试流程🌟

面试成功不是难事

🍏《2021年金九银十最新的VUE面试题☀️《❤️记得收藏❤️》》🍏

🍏《只要你认真看完一万字☀️Linux操作系统基础知识☀️分分钟钟都吊打面试官《❤️记得收藏❤️》》🍏

🍏《❤️用一万字给小白全面讲解python编程基础问答❤️《😀记得收藏不然看着看着就不见了😀》》🍏

✨有关各大公司面试题、面试流程欢迎各位查看个人主页✨

💫点击直接资料领取💫

​ 这里有各种学习资料还有有有趣好玩的编程项目，更有难寻的各种资源。 ​ ​

❤️关注苏州程序大白公众号❤️

👇 👇👇

以上是关于一文彻底解析数据库设计思路的主要内容，如果未能解决你的问题，请参考以下文章

揭秘：一文彻底搞定高可用「异地多活」架构设计

一文彻底了解元数据管理与架构设计

一文彻底了解元数据管理与架构设计

面经最频繁的单例模式一文彻底整明白

一文让你彻底理解SQL关联子查询

片段（Java） | 机试题+算法思路+考点+代码解析 2023