并查集（UnionFind）

Posted 2021-12-20 Debroon

并查集（UnionFind）

• • 基本介绍
  • 合并优化
  • 基于 Size 优化
  • 基于 Rank 优化
  • 基于路径压缩优化

 

---

基本介绍

并查集可以高效的回答，网络中任意的俩个点是否连接，因为只关心是否连接，不关心是怎么连接，所以没有做无用功。

所谓并查集（UnionFind），就是由俩种操作组合而成：

• 并：union
• 查：find

并查集也是树，不过不是父亲指向孩子，而是孩子指向父亲。

把每一个元素，看做是一个节点并且指向自己的父节点，根节点指向自己。

我们通过一个数组记录这份关系：

数组编号	0	1	2	3	4	5	6
元素所属集合编号	0	1	2	3	4	5	6

一开始，1的编号是1，2的编号是2，N的编号是N：

• 编号不同，就在不同组
• 编号相同，就在同一组

如果我们把俩个元素合并，如 5 -> 6，相应的元素 5 所属的集合编号就变成 6：

数组编号	0	1	2	3	4	5	6
元素所属集合编号	0	1	2	3	4	6	6

#include<stdio.h>

int uset[1024];                        // 存放每个元素的编号，编号相同的元素，属于同一组
void makeSet( int size )              // 初始化并查集
	for( int i=0; i<size; i ++ )
    	uset[i] = i;                   // 1的编号是1，2的编号是2，N的编号是N，编号不同，就在不同组


int find(int x)                       // 查：查找元素 x 所对应的集合编号
    assert( x >= 0 && x < 1024 );      
    return uset[x];


bool isConnected( int x, int y )      // 查：查看元素 x 和 元素 y 是否所属一个集合
	return find(x) == find(y);         


void union( int x, int y )            // 并：合并俩个元素
	int xID = find(x);
	int yID = find(y);
	if( xID == yID )
		return;
		
	for( int i=0; i<1024; i++ )        // 合并过程需要遍历一遍所有元素
		if( uset[i] == xID );          // 遍历到 x 的数组编号
			uset[i] = yID;             // 将两个元素的所属集合编号合并

我们用数组的形式表示并查集，实际操作过程中查找的时间复杂度为 $O(1)$，但连接效率并不高 $O(n)$。
 

---

合并优化

合并效率不高的原因在于，我们需要遍历一次数组。

• 其实判断两个元素是否连接，只需要判断根节点是否相同即可。

如下图所示这种情况，合并俩个元素，让 9 -> 4。

为了高效合并，实际我们并不会让 9 -> 4，而是让 9 -> 8（根节点），避免形成一个链表，体现不出树的优势。

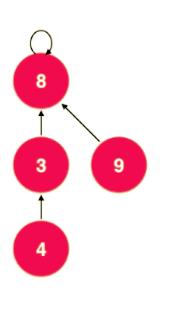
这样的实现方式，会让 find 这一步复杂一些，我们需要获取根节点的编号，而不是当前元素的编号。

int find( int x )                     // 查：查找元素 x 所对应的集合编号
	assert( x >= 0 && x < 1024 );
	return uset[x];                  

int find(int x)
    assert( x >= 0 && x < 1024 );
    while( x != uset[x] )              // 不断去查询自己的父亲节点, 直到到达根节点，根节点的特点: uset[x] == x
        x = uset[x];                    
    return x;

之前只需要比较俩个元素所属集合的编号是否相同，现在就需要查俩个节点各自所在的根节点是谁，如果俩者的根节点相同，说明俩个元素相连。

void union( int x, int y )            // 并：合并俩个元素
	int xRoot = find(x);
	int yRoot = find(y);
	if( xRoot == yRoot )
		return;

	uset[xRoot] = yRoot;               //  使其中一个根节点指向另外一个根节点，两个集合就合并了

完整代码：

#include<stdio.h>

int uset[1024];                        // 存放每个元素的编号，编号相同的元素，属于同一组
void makeSet( int size )              // 初始化并查集
	for( int i=0; i<size; i ++ )
    	uset[i] = i;                   // 1的编号是1，2的编号是2，N的编号是N，编号不同，就在不同组


int find(int x)
    assert( x >= 0 && x < 1024 );
    while( x != uset[x] )              // 不断去查询自己的父亲节点, 直到到达根节点，根节点的特点: uset[x] == x
        x = uset[x];                    
    return x;


bool isConnected( int x, int y )      // 查：查看元素 x 和 元素 y 是否所属一个集合
	return find(x) == find(y);         


void union( int x, int y )            // 并：合并俩个元素
	if( isConnected(x, y) )            // 如果属于相同集合
    	return;                        // 就不需要合并了
	uset[x] = y;                       // 使其中一个根节点指向另外一个根节点，两个集合就合并了

时间复杂度为 $O(h)$ 复杂度，$h$ 为树的高度。

大多数时候，树的高度 $h$ 比数组长度 $n$ 要小很多，但，尽管如此，我们这样写的并查集，可能会让树退化成链表，最坏的时间复杂度堪比 $O(n)$。
 

---

基于 Size 优化

如下图所示这种情况，合并俩个元素，让 9 -> 4。

为了高效合并，实际我们并不会让 9 -> 4，而是让 9 -> 8（根节点），避免形成一个链表，体现不出树的优势。

但我们上面的代码实现 uset[xRoot] = yRoot，却是让 8 -> 9 了，形成了一个单链表。

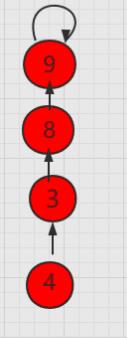
解决这个问题其实很简单，在进行合并操作时候，根据两个元素所在树的元素个数不同判断合并方向。

• 构造并查集的时候需要多一个参数，size 数组，size[i] 表示以 i 为根的集合中元素个数。
• 在进行合并操作时候，根据两个元素所在树的元素个数不同判断合并方向
• 把元素少的集合根节点指向元素多的根节点

完整代码：

#include<stdio.h>

int uset[1024];                        // 存放每个元素的编号，编号相同的元素，属于同一组
int size[1024];                        // 表示以i为根的集合中元素个数，全局变量默认 = 0

void makeSet( int _size )             // 初始化并查集
	for( int i=0; i<_size; i ++ )
    	uset[i] = i;                   // 1的编号是1，2的编号是2，N的编号是N，编号不同，就在不同组


int find(int x)
    assert( x >= 0 && x < 1024 );
    while( x != uset[x] )              // 不断去查询自己的父亲节点, 直到到达根节点，根节点的特点: uset[x] == x
        x = uset[x];                    
    return x;


void union( int x, int y )            // 并：合并俩个元素
	int xRoot = find(x);
	int yRoot = find(y);
	if( xRoot == yRoot )
		return;

	// 根据两个元素所在树的元素个数不同判断合并方向
    // 将元素个数少的集合合并到元素个数多的集合上
	if( size[xRoot] < size[yRoot] ) 
        uset[xRoot] = yRoot;
        size[yRoot] += sz[xRoot];
     else 
        uset[yRoot] = xRoot;
        size[xRoot] += size[yRoot];
    

 

---

基于 Rank 优化

并查集基于 size 的优化，但是某些场景下，也会存在某些问题。

• size 的优化，元素少的集合根节点指向元素多的根节点。

操完后，层数变为 4，比之前增多了一层。

由此可知，依靠集合的 size 判断指向并不是完全正确的，更准确的是，根据两个集合层数，层数少的集合根节点指向层数多的集合根节点。

在并查集的属性中，把 size 数组改为 rank 数组，rank[i] 表示以 i 为根的集合所表示的树的层数。

#include<stdio.h>

int uset[1024];                        // 存放每个元素的编号，编号相同的元素，属于同一组
int rank[1024];                        // 表示以i为根的集合所表示的树的层数，全局变量默认 = 0

void makeSet( int size )              // 初始化并查集
	for( int i=0; i<size; i ++ )
    	uset[i] = i;                   // 1的编号是1，2的编号是2，N的编号是N，编号不同，就在不同组
    	rank[i] = 1;


int find(int x)
    assert( x >= 0 && x < 1024 );
    while( x != uset[x] )              // 不断去查询自己的父亲节点, 直到到达根节点，根节点的特点: uset[x] == x
        x = uset[x];                    
    return x;


void union( int x, int y )            // 并：合并俩个元素
	int xRoot = find(x);
	int yRoot = find(y);
	if( xRoot == yRoot )
		return;

	// 根据两个元素所在树的rank不同判断合并方向
    // 将rank低的集合合并到rank高的集合上
	if( rank[xRoot] < rank[yRoot] ) 
        uset[xRoot] = yRoot;
     else if ( rank[yRoot] < rank[xRoot]) 
        uset[yRoot] = xRoot;
     else  
        uset[xRoot] = yRoot;
        rank[yRoot] += 1;              // 此时, 维护rank的值
    

 

---

基于路径压缩优化

如果只看节点之间是否相互联通，其实最好情况 = 最坏情况 = 一般情况，但他们的层数不一样，会导致并查集复杂度不一样。

所以，并查集里的 find 函数里可以进行路径压缩，是为了更快速的查找一个点的根节点。

对于一个集合树来说，它的根节点下面可以依附着许多的节点，因此，我们可以尝试在 find 的过程中，从底向上，如果此时访问的节点不是根节点的话，那么我们可以把这个节点尽量的往上挪一挪，减少数的层数，这个过程就叫做路径压缩。

如下图中，最坏情况下 find(4) 的过程就可以路径压缩，让树的层数更少。

节点 2 向上寻找，也不是根节点，那么把元素 2 指向原来父节点的父节点，操后后树的层数相应减少了一层：

// uset[] 改为 parent[]
int find(int x) 
    assert( x >= 0 && x < 1024 );
    while( x != parent[x] )                   // 不是根节点
        parent[x] = parent[parent[x]];         // 指向原来父节点的父节点
        x = parent[x];                         // 返回根节点
    
    return x;

上述路径压缩并不是最优的方式，我们可以把最初的树压缩成最好情况，层数是最少的。

int find( int x )                     // 查：查找元素 x 所对应的集合编号
	if( x != uset[x] )                 // 直到找到根节点，所有节点指向的节点
    	uset[x] = find( uset[x] );     // 从当前孩子节点继续找父亲节点
	return uset[x];                  

完整代码：

#include<stdio.h>

int uset[1024];                        // 存放每个元素的编号，编号相同的元素，属于同一组
void makeSet( int size )              // 初始化并查集
	for( int i=0; i<size; i ++ )
    	uset[i] = i;                   // 1的编号是1，2的编号是2，N的编号是N，编号不同，就在不同组


int find( int x )                     // 查：查找元素 x 所对应的集合编号
	if( x != uset[x] )                 // 直到找到根节点，所有节点指向的节点
    	uset[x] = find( uset[x] );     // 从当前孩子节点继续找父亲节点
	return uset[x];                  


bool isConnected( int x, int y )      // 查：查看元素 x 和 元素 y 是否所属一个集合
	return find(x) == find(y);         


void union( int x, int y )            // 并：合并俩个元素
	int xRoot = find(x);
	int yRoot = find(y);
	if( xRoot == yRoot )
		return;

	// 根据两个元素所在树的rank不同判断合并方向
    // 将rank低的集合合并到rank高的集合上
	if( rank[xRoot] < rank[yRoot] ) 
        uset[xRoot] = yRoot;
     else if ( rank[yRoot] < rank[xRoot]) 
        uset[yRoot] = xRoot;
     else  
        uset[xRoot] = yRoot;
        rank[yRoot] += 1;              // 此时, 维护rank的值