水很深的深度学习-Task03前馈神经网络

Posted 2021-12-18 GoAl的博客

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了水很深的深度学习-Task03前馈神经网络相关的知识，希望对你有一定的参考价值。

本文参考

神经元模型

在前馈神经网络中，各神经元分别属于不同的层。每一层的神经元可以接收前一层神经元的信号，并产生信号输出到下一层。第 0 层叫输入层，最后一层叫输出层，其它中间层叫做隐藏层，相邻两层的神经元之间为全连接关系，也称为全连接神经网络(F N N FNNFNN)，表现形式如下图所示。

我们用下面的记号来描述一个前馈神经网络：

神经网络的发展历程

神经元(M-P)

1943 年，美国神经生理学家沃伦·麦卡洛克( Warren McCulloch ) 和数学家沃尔特 ·皮茨(Walter Pitts )对生物神经元进行建模，首次提出了一种形式神经元模型，并命名为McCulloch-Pitts模型，即后来广为人知的M-P模型。

在M-P模型中，神经元接受其他n个神经元的输入信号(0或1)，这些输入信号经过权重加权并求和，将求和结果与阈值(threshold) θ 比较，然后经过激活函数处理，得到神经元的输出。

y=f\\left(\\sum_i=1^n \\omega_i j x_i-\\theta\\right)y=f(i=1∑nωijxi−θ)

M-P 模型可以表示多种逻辑运算，如取反运算、逻辑或、逻辑与。

取反运算可以用单输入单输出模型表示，即如果输入为0则输出1，如果输入为1则输出0。由M-P模型的运算规则可得 w = -2， θ = -1w=−2，θ=−1.

逻辑或与逻辑与运算可以用双输入单输出模型表示。以逻辑与运算为例， w_1=1，w_2=1, θ =1.5w1=1，w2=1,θ=1.5.

网络结构

人工神经网络由神经元模型构成，这种由许多神经元组成的信息处理网络具有并行分布结构。

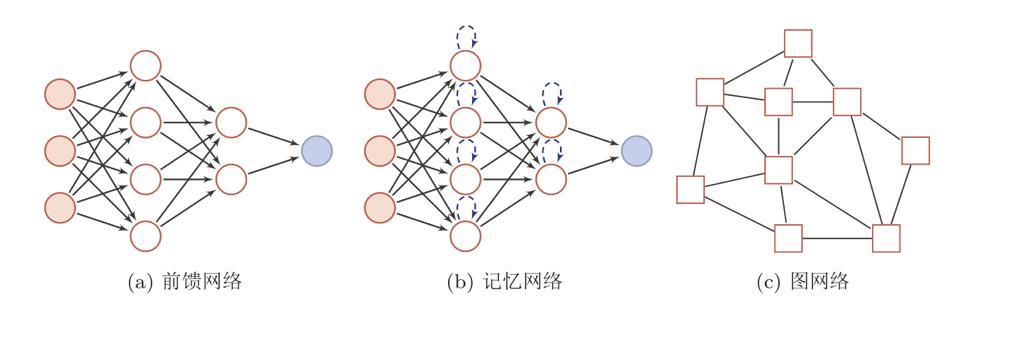
其中圆形节点表示一个神经元，方形节点表示一组神经元。

感知器

单层感知器

1958 年，罗森布拉特( Roseblatt )提出了感知器，与 M-P 模型需要人为确定参数不同，感知器能够通过训练自动确定参数。训练方式为有监督学习，即需要设定训练样本和期望输出，然后调整实际输出和期望输出之差的方式(误差修正学习)。

\\beginaligned w_i & \\leftarrow w_i+\\alpha(r-y) x \\\\ \\theta & \\leftarrow \\theta-\\alpha(r-y) \\endalignedwiθ←wi+α(r−y)x←θ−α(r−y)

其中，\\alphaα 是学习率，rr 和 yy 分别是期望输出和实际输出。

感知器权重调整的基本思路：

实际输出 y 与期望输出 r 相等时，w 和 θ 不变
实际输出 y 与期望输出 r 不相等时，调整 w 和 θ 的值

\\beginaligned w_i & \\leftarrow w_i+\\alpha(r-y) x \\\\ \\theta & \\leftarrow \\theta-\\alpha(r-y) \\endalignedwiθ←wi+α(r−y)x←θ−α(r−y)

下面给出感知器模型的训练过程

多层感知器

单层感知器只能解决线性可分问题，而不能解决线性不可分问题；为了解决线性不可分问题，我们需要使用多层感知器。

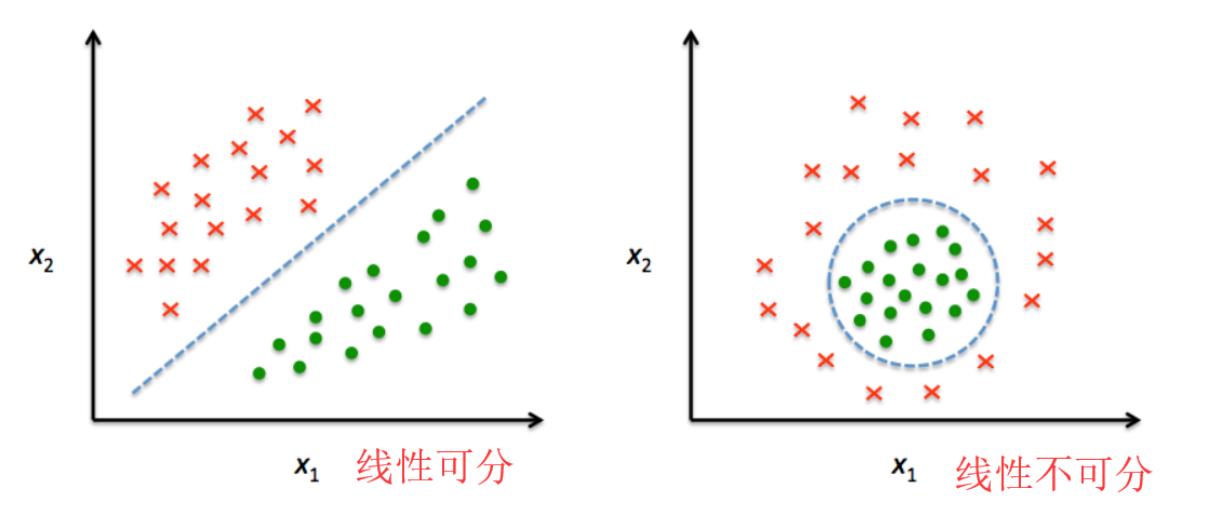
多层感知器指的是由多层结构的感知器递阶组成的输入值向前传播的网络，也被称为前馈网络或正向传播网络。

以三层结构的多层感知器为例，它由输入层、中间层及输出层组成

与M-P模型相同，中间层的感知器通过权重与输入层的各单元相连接，通过阈值函数计算中间层各单元的输出值
中间层与输出层之间同样是通过权重相连接

BP算法

多层感知器的训练使用误差反向传播算法(Error Back Propagation)，即BP算法。BP算法最早有沃博斯于1974年提出，鲁梅尔哈特等人进一步发展了该理论。

BP算法的基本过程

前向传播计算：由输入层经过隐含层向输出层的计算网络输出
误差反向逐层传递:网络的期望输出与实际输出之差的误差信号由输出层经过隐含层逐层向输入层传递
由“前向传播计算”与“误差反向逐层传递”的反复进行的网络训练过程

BP算法就是通过比较实际输出和期望输出得到误差信号，把误差信号从输出层逐层向前传播得到各层的误差信号，再通过调整各层的连接权重以减小误差。权重的调整主要使用梯度下降法：

\\Delta w = -\\alpha \\frac\\partial E\\partial wΔw=−α∂w∂E

激活函数

通过误差反向传播算法调整多层感知器的连接权重时，一个瓶颈问题就是激活函数：

M-P 模型中使用阶跃函数作为激活函数，只能输出 0或 1，不连续所以不可导
为了使误差能够传播，鲁梅尔哈特等人提出使用可导函数Sigmoid作为激活函数

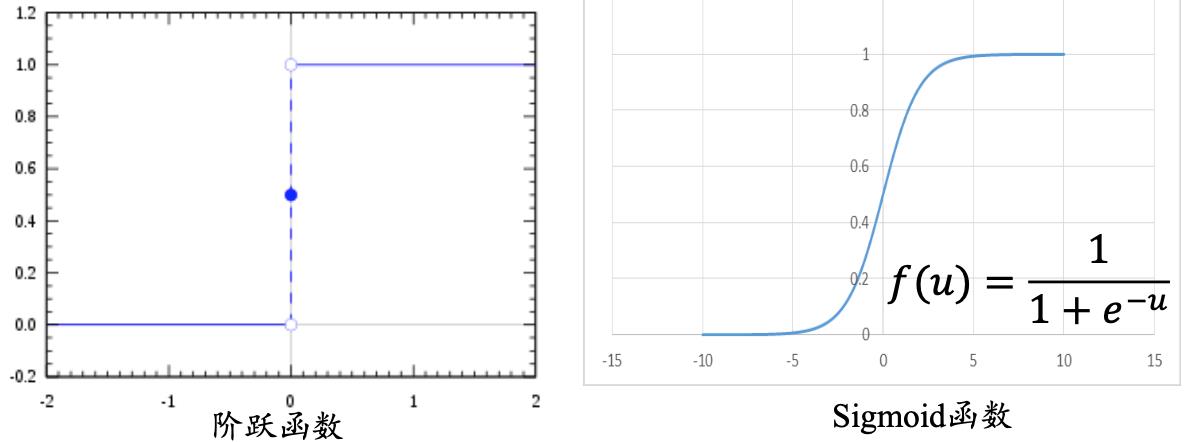
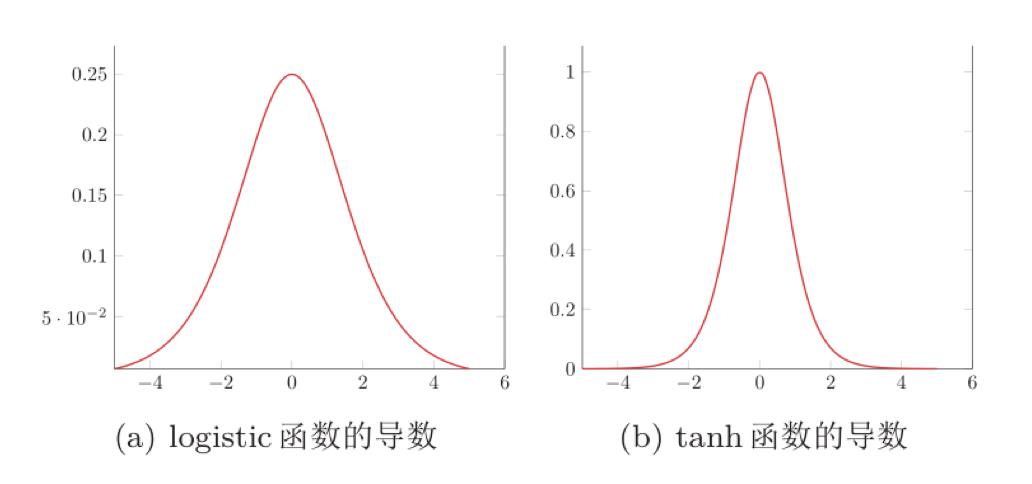
Sigmoid函数的导数：\\fracdf(u)du = f(u)(1-f(u))dudf(u)=f(u)(1−f(u))

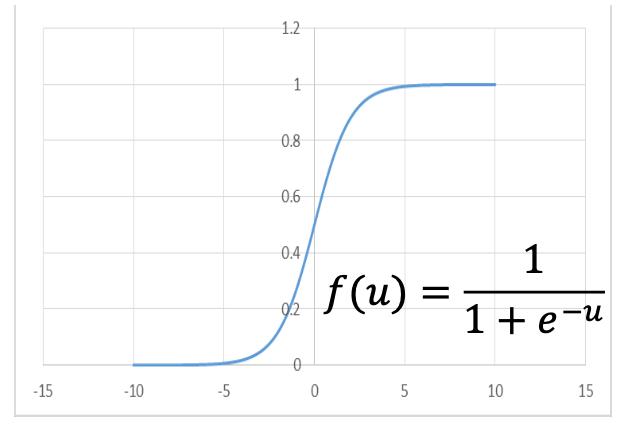
其他常见的激活函数：ReLU (Rectified Linear Unit，修正线性单元)和tanh等

BP算法示例

以包含一个中间层和一个输出单元 yy 的多层感知器为例：w_1ijw1ij 表示输入层与中间层之间的连接权重，w_2j1w2j1 表示中间层与输出层之间的连接权重， ii 表示输入层单元，jj 表示中间层单元。

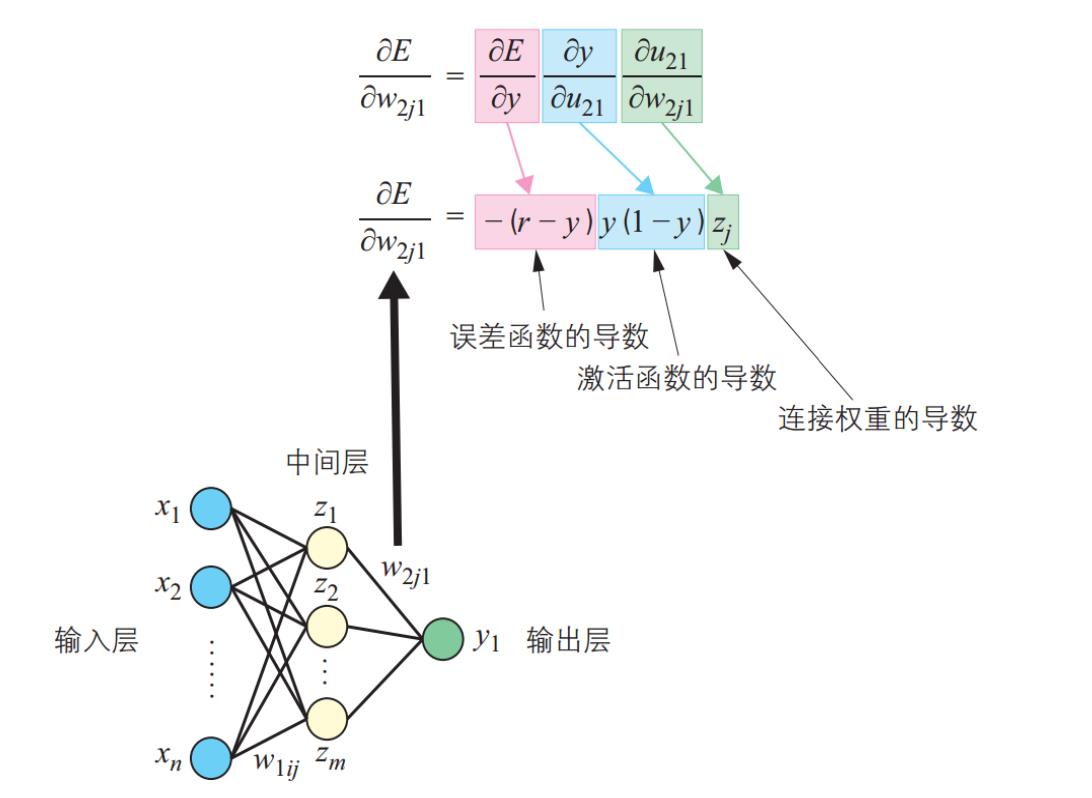
首先调整中间层与输出层之间的连接权重，其中 y=f(u)y=f(u)， ff 是激活函数，u_21 = \\sum_j = 1^mw_2j1z_ju21=∑j=1mw2j1zj，把误差函数 E 对连接权重w_2j1w2j1 的求导展开成复合函数求导：

\\beginarrayc\\frac\\partial E\\partial w_2 j 1 =\\frac\\partial E\\partial y \\frac\\partial y\\partial u_21 \\frac\\partial u_21\\partial w_2 j 1 \\\\ =-(r-y) y(1-y) z_j\\endarray∂w2j1∂E=∂y∂E∂u21∂y∂w2j1∂u21=−(r−y)y(1−y)zj

这里 z_jzj 表示的是中间层的值。

第二，中间层到输出层的连接权重调整值如下所示：

\\Delta w_2 j 1=\\alpha(r-y) y(1-y) z_jΔw2j1=α(r−y)y(1−y)zj

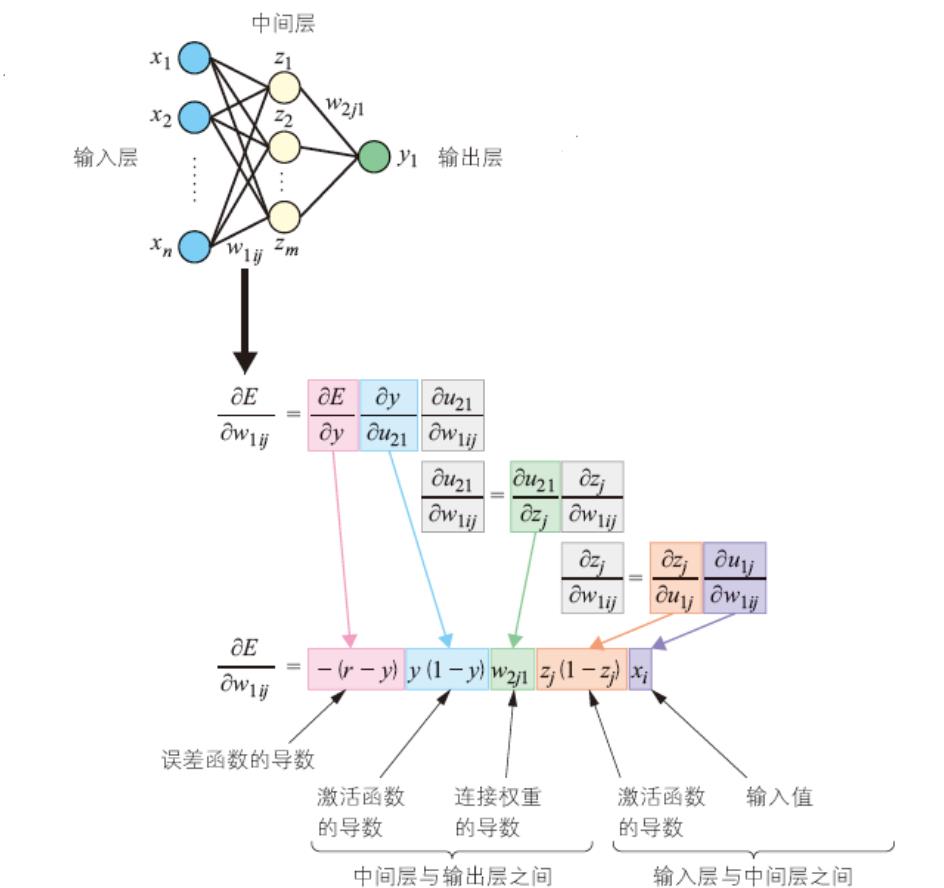
第三，调整输入层与中间层之间的连接权重

\\beginaligned \\frac\\partial E\\partial w_1 i j &=\\frac\\partial E\\partial y \\frac\\partial y\\partial u_21 \\frac\\partial u_21\\partial w_1 i j \\\\ &=-(r-y) y(1-y) \\frac\\partial u_21\\partial w_1 i j \\endaligned∂w1ij∂E=∂y∂E∂u21∂y∂w1ij∂u21=−(r−y)y(1−y)∂w1ij∂u21

中间层到输出层