基于ICP算法计算点集之间的变换矩阵（旋转平移）

Posted 2021-12-17 一颗小树x

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了基于ICP算法计算点集之间的变换矩阵（旋转平移）相关的知识，希望对你有一定的参考价值。

前言

本文主要是计算两个激光雷达之间的变换矩阵，即计算两组点云之间的变换矩阵。其中处理的点云数据主要是由x,y,z,intensity组成的，代表空间位置x,ry,z 和每个点云对应的反射强度intensity；

这里计算点集之间的变换矩阵，用到每个点云的x,y,z信息，可表示为n*3的数组；两组激光雷达点云，可以表示为2和n*3的数组。

首先使用ICP点云匹配算法，计算两组点云之n*3的数组间对应的点；然后基于SVD算法求出两个对应点集合的旋转矩阵R和转移矩阵t。

一、基于ICP匹配对应点

基于点的匹配算法中常用最多的是 ICP（Iterative Closest Point）算法；其实质是基于两个集合中最近点对的搜索，并且估计将它们对齐的“刚性变换”。然后，将刚性变换应用于一个集合的点，并迭代该过程直到收敛。

优点：原理简单、易于理解和实现，同时配准精度较高。

弊端：ICP 算法在迭代初期就必须确定初始位置，如果初始位置估计不准确，与实际位置相差较大，则可能会产生局部最优解。并且，ICP 算法在每次迭代时都要对点集内所有点进行对应点搜索。

应用：ICP 算法不需要事先对目标进行特征提取和分割，可以直接对点云进行处理。

使用ICP进行点云配准，基本思路是：对于两片待配准的点云，首先寻找两个点云中的对应点间的对应关系，计算出两片点云间的坐标变换参数，然后通过三维刚体变换，将两片待配准点云的坐标系调整到一致，从而完成两片点云在三维空间中的配准。

ICP 配准算法流程图，如下所示：

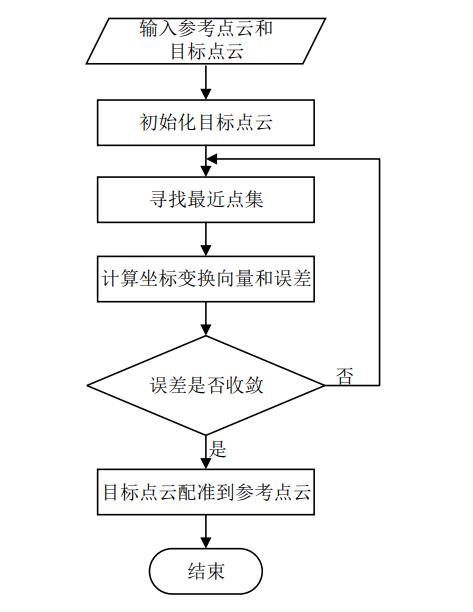
在迭代初期，数据点可能和其对应点距离很远，但随着迭代次数的增加它们距离越来越近。ICP 算法可以单调收敛到局部最小值，可能导致陷入局部极值，所以初值的选取尤为重要。

二、计算变换矩阵

假设激光雷达1的点云数据，表示为A数组，结构是n*3；激光雷达2的点云数据，表示为B数组，结构也是n*3；A和B数组已经通过ICP算法，进行一一匹配了。

注意：这里的点最少需要3个，即n>=3；点多一些，计算得更精准一些。

2.1 思路

对于无噪声数据，两个点集之间的旋转矩阵R 和平移向量t，可以表示为：

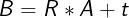（R 是一个 3×3 旋转矩阵，t 是 1×3平移向量。）

对于有噪声数据，它将最小化最小二乘误差，两个点集之间的旋转矩阵R 和平移向量t，可以表示为：

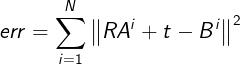
无噪声数据、或有噪声数据，计算R和t，通常都需要三步：

计算点集合的中心点（质心）
将点集合移动到原点，然后找到最优旋转矩阵R
计算转移矩阵t

2.2 计算中心点

这里是点的平均值，计算如下：

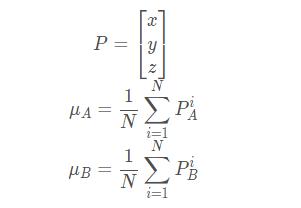
2.3 将点集合移动到原点

需要将点集重新中心化，生成新点集合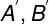，公式如下：

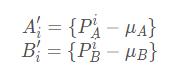
2.4 计算协方差矩阵H

计算点集之间的协方差矩阵H，公式如下：

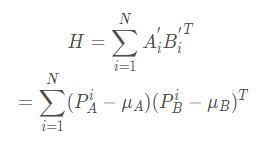
2.5 计算旋转矩阵R

通过SVD方法获得矩阵的U、S和V,可以计算点集之间的旋转矩阵R，公式如下：

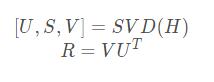
2.6 计算平移向量t

通过R可以获得转移矩阵t，公式如下：

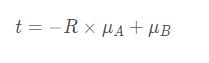
关于SVD补充一下：

奇异值分解（SVD）维基百科：https://en.wikipedia.org/wiki/Singular_value_decomposition

SVD的数学推导文档：https://igl.ethz.ch/projects/ARAP/svd_rot.pdf

三、实现代码案例

大佬们有相关的代码开源了，Python实现的：GitHub - ClayFlannigan/icp: iterative closest point

这里考虑了有噪声的数据；

import numpy as np
from sklearn.neighbors import NearestNeighbors


def best_fit_transform(A, B):
    '''
    计算在 m 个空间维度上映射对应点 A 到 B 的最小二乘最佳拟合变换
     输入：
       A：对应点的Nxm numpy数组
       B：对应点的Nxm numpy数组
     返回：
       T：(m+1)x(m+1) 将 A 映射到 B 的齐次变换矩阵
       R：mxm 旋转矩阵
       t: mx1 平移向量
    '''

    assert A.shape == B.shape

    # 获取维数
    m = A.shape[1]

    # 将点转换为它们的质心（中心点）
    centroid_A = np.mean(A, axis=0)
    centroid_B = np.mean(B, axis=0)
    AA = A - centroid_A
    BB = B - centroid_B

    # rotation matrix
    H = np.dot(AA.T, BB)
    U, S, Vt = np.linalg.svd(H)
    R = np.dot(Vt.T, U.T)

    # special reflection case
    if np.linalg.det(R) < 0:
       Vt[m-1,:] *= -1
       R = np.dot(Vt.T, U.T)

    # translation
    t = centroid_B.T - np.dot(R,centroid_A.T)

    # homogeneous transformation
    T = np.identity(m+1)
    T[:m, :m] = R
    T[:m, m] = t

    return T, R, t


def nearest_neighbor(src, dst):
    '''
    为 src 中的每个点在 dst 中找到最近的（欧几里得）邻居
     输入：
         src: Nxm 点数组
         dst: Nxm 点数组
     输出：
         距离：最近邻居的欧几里德距离
         索引：最近邻居的 dst 索引 
    '''

    assert src.shape == dst.shape

    neigh = NearestNeighbors(n_neighbors=1)
    neigh.fit(dst)
    distances, indices = neigh.kneighbors(src, return_distance=True)
    return distances.ravel(), indices.ravel()


def icp(A, B, init_pose=None, max_iterations=20, tolerance=0.001):
    '''
    迭代最近点方法：找到将点 A 映射到点 B 的最佳拟合变换
     输入：
         A: Nxm numpy 源 mD 点数组
         B：目标 mD 点的 Nxm numpy 数组
         init_pose: (m+1)x(m+1) 齐次变换
         max_iterations: max_iterations 后退出算法
         tolerance：容差收敛标准
     输出：
         T：将 A 映射到 B 的最终齐次变换
         距离：最近邻居的欧几里得距离（误差）
         i：要收敛的迭代次数 
    '''

    assert A.shape == B.shape

    # 获取维数
    m = A.shape[1]

    # 使点同种类的(points homogeneous)，复制它们以保持原件
    src = np.ones((m+1,A.shape[0]))
    dst = np.ones((m+1,B.shape[0]))
    src[:m,:] = np.copy(A.T)
    dst[:m,:] = np.copy(B.T)

    # 应用初始姿态估计
    if init_pose is not None:
        src = np.dot(init_pose, src)

    prev_error = 0

    for i in range(max_iterations):
        # 找到当前源点和目标点之间的最近邻居
        distances, indices = nearest_neighbor(src[:m,:].T, dst[:m,:].T)

        # 计算当前源点和最近目标点之间的变换
        T,_,_ = best_fit_transform(src[:m,:].T, dst[:m,indices].T)

        # 更新当前源  矩阵相乘 T*src
        src = np.dot(T, src)

        # 检查错误
        mean_error = np.mean(distances)
        if np.abs(prev_error - mean_error) < tolerance:
            break
        prev_error = mean_error

    # 计算最终变换
    T,_,_ = best_fit_transform(A, src[:m,:].T)

    return T, distances, i

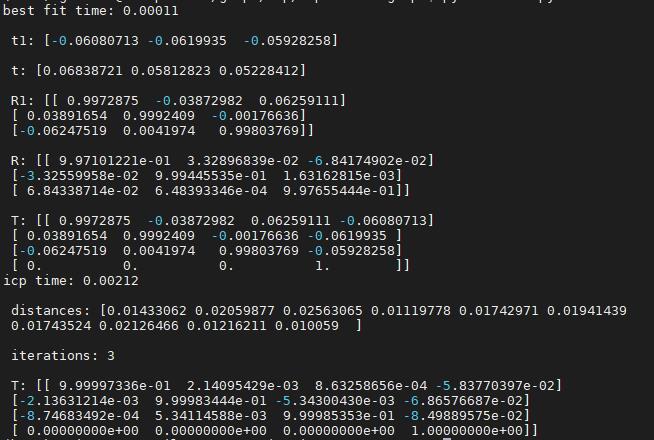
效果：