由一道考研基础题引发的关于对(函数导数符号在内外的区别)f‘(x)和[f(x)]‘的区别思考
Posted 小朱爱数学也爱编程
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了由一道考研基础题引发的关于对(函数导数符号在内外的区别)f‘(x)和[f(x)]‘的区别思考相关的知识,希望对你有一定的参考价值。
笔者今天在上课的时候,由于一道题和老师解法大相径庭而陷入思考
题目如下:
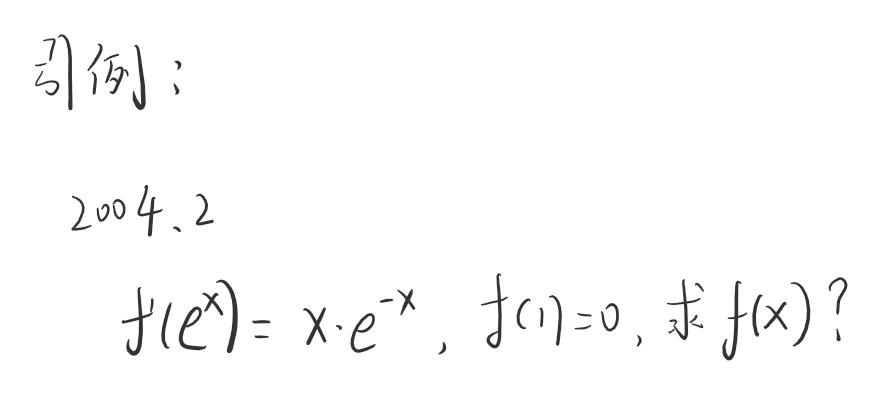
这是道02年的数学考研题目填空题第二道,事后想想确实是道非常基础的题目。
下面先奉上老师的标准解法:
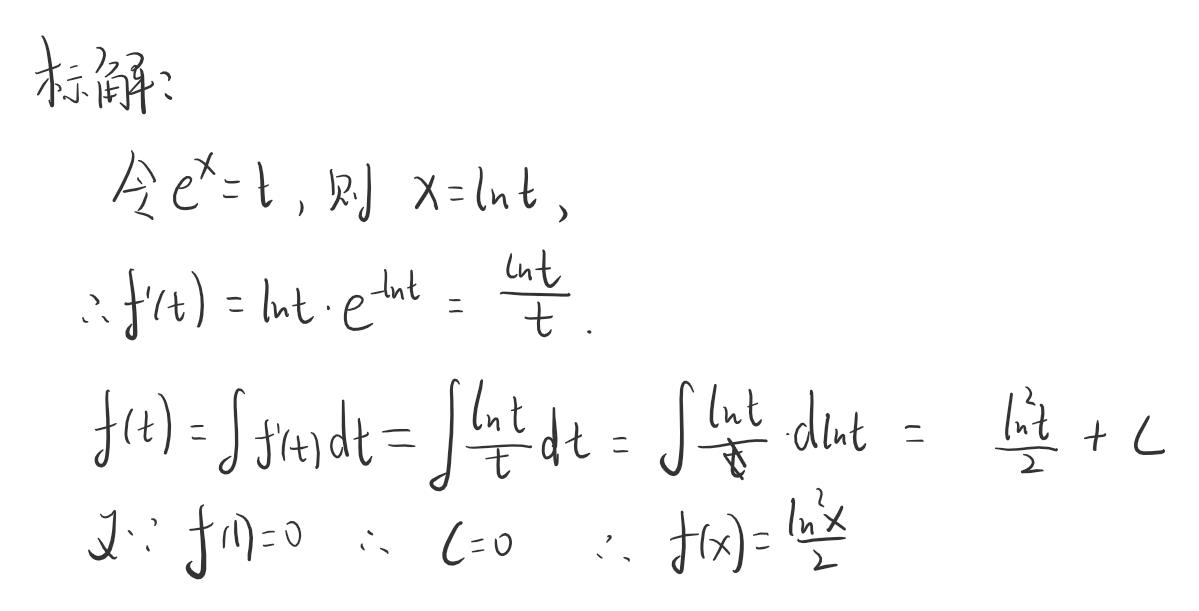
很经典的换元思想。
当时我纠结的地方在于,我下面的写法为何是错误。

笔者想把原题的左边式子看成复合函数求导的内导,根据复合函数的求导法则,只需要再乘以括号内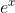 的导数也是就其本身,然后得到的就是f'(x)(整个复合导数的求导)
的导数也是就其本身,然后得到的就是f'(x)(整个复合导数的求导)
那么问题处在哪里了呢?
下面我们再引出一个问题,也是这篇文章的核心
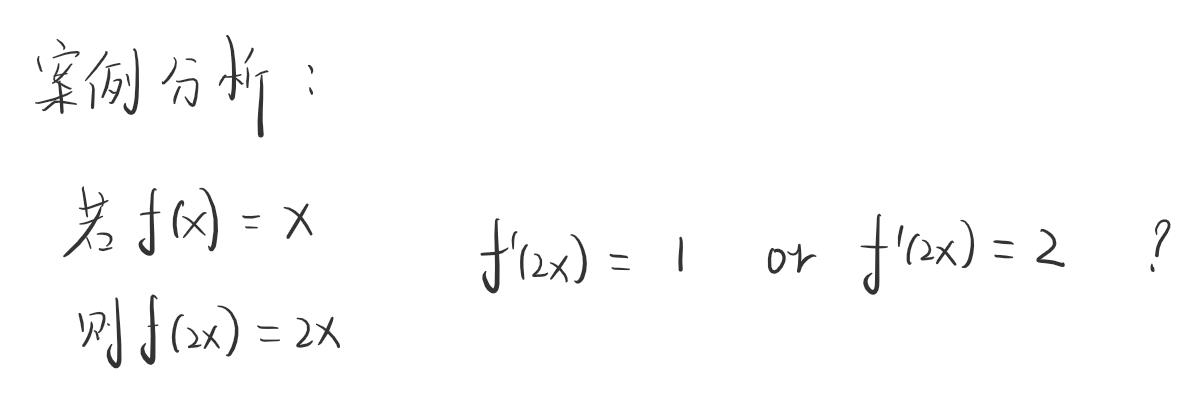
错认为答案为2
其实答案是1哈哈!!
这就牵扯到我们对复合求导这一概念的刨析了。
笔者抄了一段同济课本的复合求导定义:

这个问题答案的解决核心是,这个f‘(2x)到底是等式的左边部分,还是画红线的部分
其实从形式上来看,很明显就是右边画红波浪号的形式了,
其实很多人对于这段定义都有误解
或者说其实对于f'(u)这个东西的理解有偏差 , 我们可能对大部分的复合求导都没有有问题,但是一直没有理清楚,我们求导的过程中,到底所写的部分是对于这个式子的哪个。
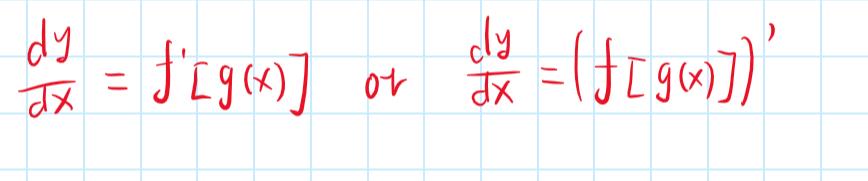
我们求的是y的导数没错,但是y的导数是上图左边,还是右边呢
答案是右边
其实f'[g(x)]本身就是f'(u),因为u=g(x),所以左边肯定是不对的
笔者充满了疑惑,在网上一直搜罗,最后找到了这个。
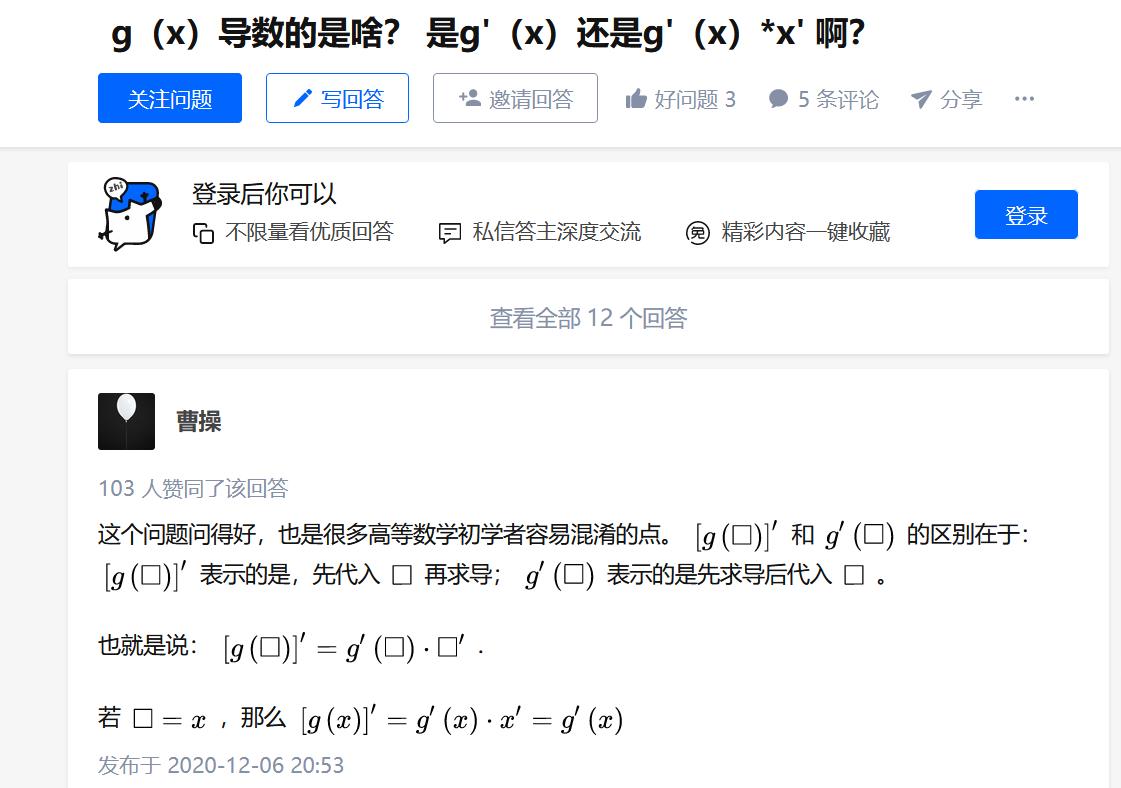
和  的区别在于:
的区别在于:  表示的是,先代入
表示的是,先代入  再求导;
再求导;  表示的是先求导后代入
表示的是先求导后代入  。
。
这句话可谓是一针见血。当然学习数学要本着探索其内在的精神。我们进一步思考含义
 ,
,
这句话其实换种方式理解,就是我们把框框看成一个整体,对框框求导。
什么意思呢,其实就是我们复合函数常说的外导,就是把框框当成x处理,在处理完后把x换成框框,是不是有点绕回去了呢哈。
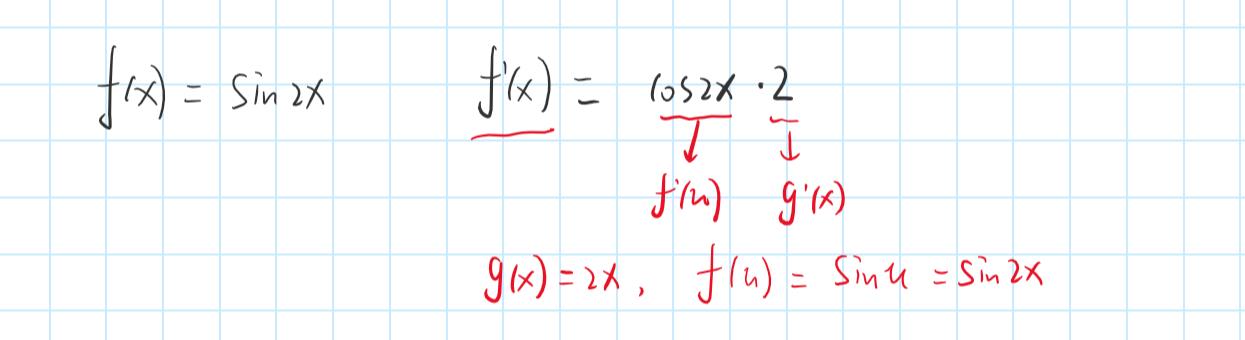
举一个我们复合函数求导的例子,大家对照着理解
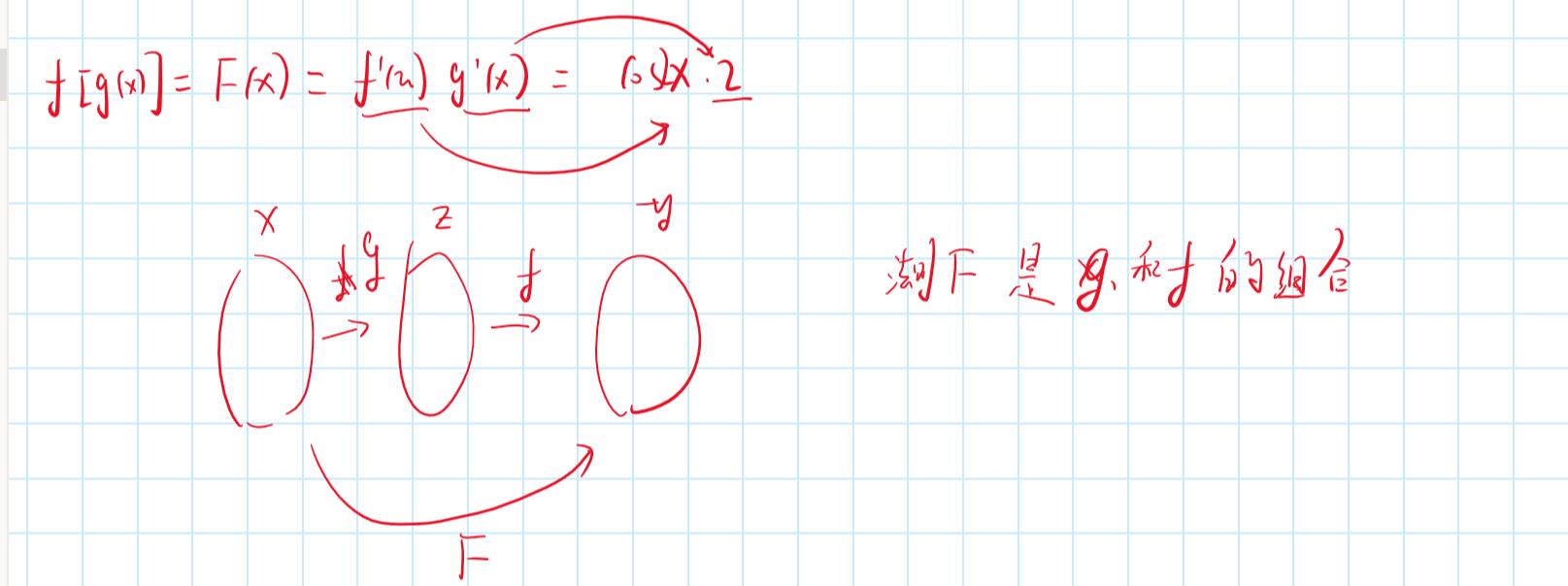
回过头来我们分析问题所在,其实是因为这样乘以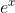 ,得到的不是f‘(x)
,得到的不是f‘(x)
而是F'(X),原来的式子仅仅只是F‘(x)=【f(g(x))】‘而不是f’(g(x))
这里的F就是f和g两种法则的复合,我用一张图片帮助大家理解。
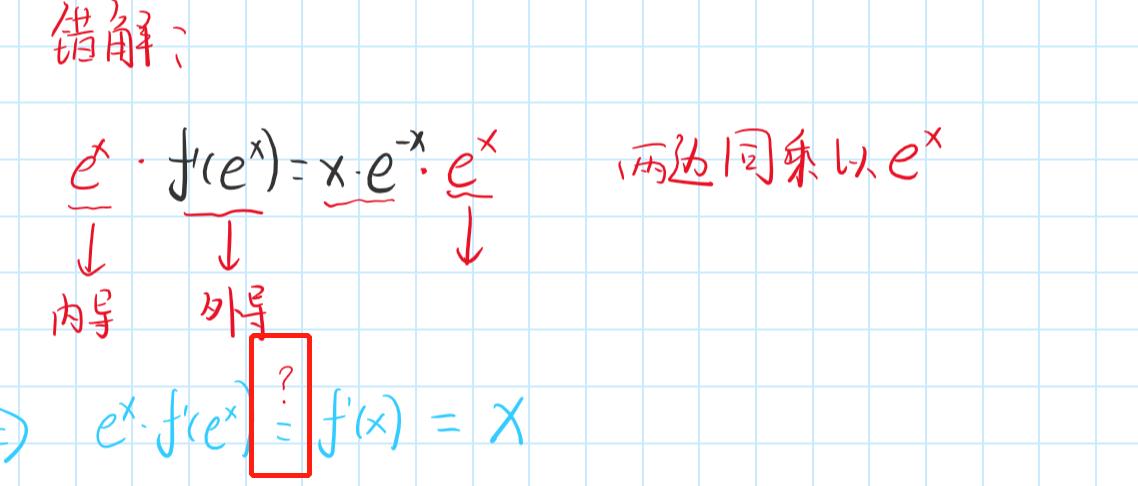
所以这里的等号根本不成立,故错误。
总结:
f‘(g(x))=f‘(t) 这里是对t求导也就是g(x)求导,或者说是f’(x)(对x求导后)中全部x换成t的结果
[f(g(x))]'=F'(X) 这里F是f和g法则的复合,是对x求导,或者说是把x换成t 也就是g(x)后再求导
以上是关于由一道考研基础题引发的关于对(函数导数符号在内外的区别)f‘(x)和[f(x)]‘的区别思考的主要内容,如果未能解决你的问题,请参考以下文章