(王道408考研数据结构)第五章树-第三节1：二叉树遍历（先序中序和后序）

Posted 2021-12-14 我擦了DJ

文章目录

• 一：二叉树遍历概述
• 二：二叉树深度优先遍历
• • （1）先序遍历-根左右(NLR)
  • （2）中序遍历-左根右(LNR)
  • （3）后序遍历-左右根(LRN)
  • 总结：三种遍历方式动图演示
• 三：二叉树的层序遍历

一：二叉树遍历概述

二叉树遍历（traversing binary tree）：从根节点开始，按照某种次序依次访问二叉树中的所有结点，使得每个结点被访问一次且仅被访问一次

• 访问： 访问是一个抽象操作，是指具体你遍历到这个节点应该做什么？比如说最简单的打印，修改值等等
• 次序：二叉树比遍历有别于普通线性结构，因为树的结点之间不存在唯一的前驱和后继的关系，下一个被访问的结点面临着不同的选择。由于选择的方式不同，遍历的次序也就不同了

二：二叉树深度优先遍历

大部分人其实都知道一些二叉树的遍历的口诀，例如

• 先序遍历是“根左右”；
• 中序遍历是“左根右”;
• 后序遍历是“左右根“”;

通过这样的口诀，能够很快的写出树的各种遍历次序，但如果问到为什么是这样，很多人却无法说清楚。

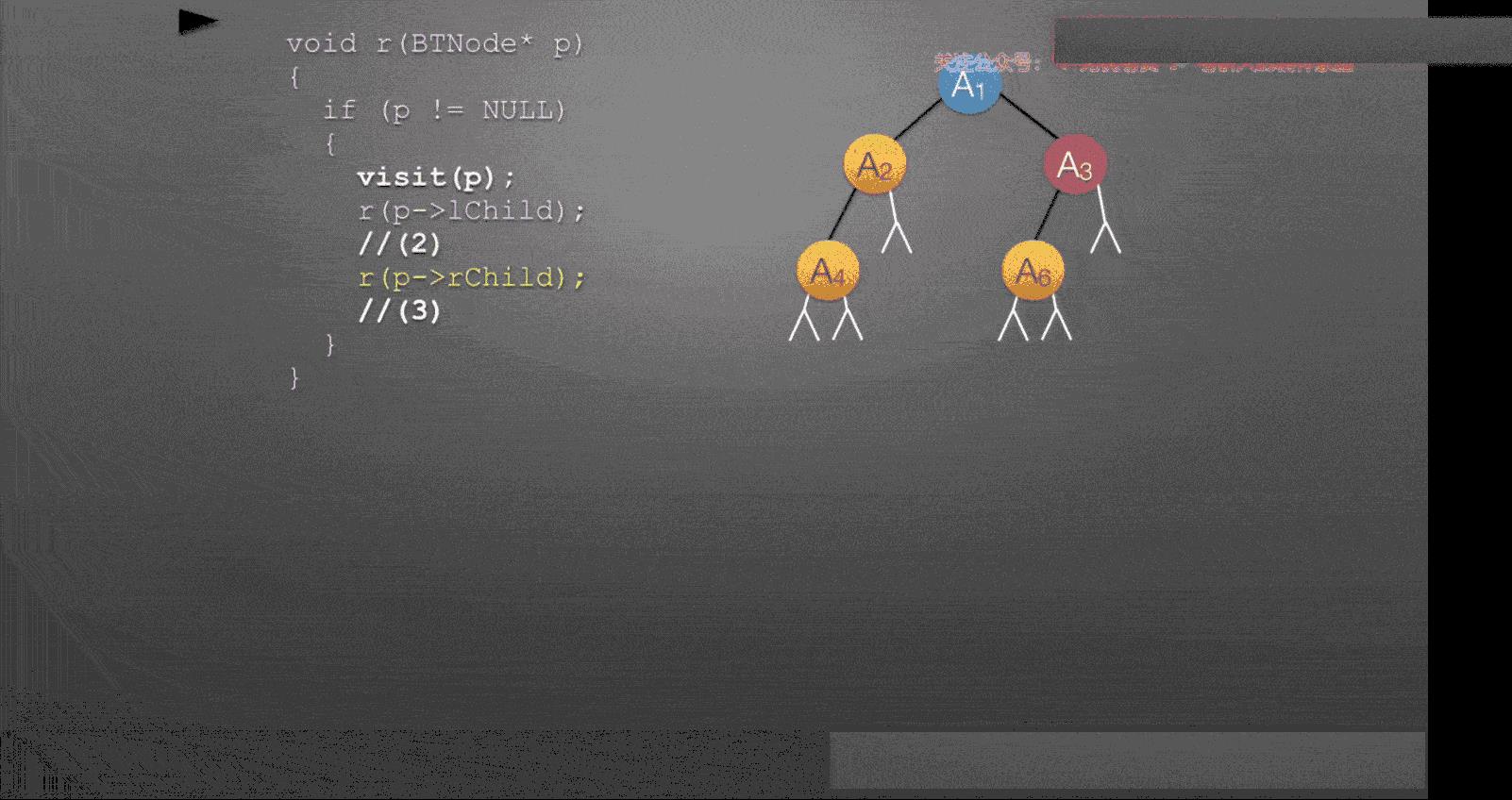
呈现出不同的遍历的方式的根本原因在于二叉树的递归结构和访问时机的不同

如下图，这三种遍历方式本质是一样的，每个结点都会经历三次访问，二叉树默认递归时其实就是先序遍历，也就是先根节点，再左，后右。而在不同时机访问，就会造成不同的遍历结果

（1）先序遍历-根左右(NLR)

先序遍历：第一次遇到这个结点访问，第二次遇到或第三次遇到跳过该结点直接访问下一个结点

• 也即：若二叉树为空，则返回空，否则先访问根节点，然后前序遍历左子树，再前序遍历右子树

先序遍历算法：二叉树定义采用的递归形式，所以其遍历代码也可以采用递归，形式极其简单

void PreOrderTraverse(BTNode* root)

	if(root==NULL)
		return NULL;
	printf("%c",root->data);//结点访问操作，也可以是其他
	PreOrderTraverse(BTNode->lchild);//再先序遍历左子树
	PreOrderTraverse(BTNode->rchild);//最后先序遍历右子树
	

接下来，我们用下面的树来说明上述代码是怎样执行的

• 1：首先调用了PreOrderTraverse(A)，由于根节点A不为空，所以执行了printf，字母A被打印
  

• 2：接着调用了PreOrderTraverse(A->lchild)，由于根节点A的左孩子不为空，所以执行了printf，字母B被打印
  

• 3：接着调用了PreOrderTraverse(B->lchild)，由于结点B的左孩子不为空，所以执行了printf，字母D被打印
  

• 4：接着调用了PreOrderTraverse(D->lchild)，由于结点D的左孩子不为空，所以执行了printf，字母H被打印
  

• 5：接着调用了PreOrderTraverse(H->lchild)，但此时结点H没有左孩子，所以被调函数传入root==NULL，直接return NULL;PreOrderTraverse(H->lchild)于是直接结束，立马执行PreOrderTraverse(H->rchild)，执行了printf，字母K被打印
  

• 6：接着调用了PreOrderTraverse(K->lchild)，访问K结点左孩子，但没有左孩子，所以调用后直接返回了NULL，然后调用PreOrderTraverse(K->rchild)，但没有右孩子，所以调用后直接返回了NULL。那么这就导致PreOrderTraverse(H->rchild)函数的结束，而PreOrderTraverse(H->rchild)的结束就导致了PreOrderTraverse(D->lchild)，于是会执行PreOrderTraverse(D->rchild)，但没有右孩子，从而导致了PreOrderTraverse(B->lchild)函数的结束，于是继续执行PreOrderTraverse(B->rchild)，执行了printf，字母E被打印
  

• 7：对于结点E来说他，它也没有左右孩子，所以访问完成之后PreOrderTraverse(B->rchild)结束，它的结束自然导致了PreOrderTraverse(A->lchild)的结束，于是A的左子树访问完毕，现在开始右子树，因此PreOrderTraverse(A->rchild)，执行了printf，字母C被打印
  

• 8：后续访问过程不再赘述。遍历结果为$A-B-D-H-K-E-C-F-I-G-J$

（2）中序遍历-左根右(LNR)

中序遍历：第一次遇到结点跳过，第二次再遇到结点访问，第三次遇到跳过

• 也即：若树为空，则返回空，否则从根节点开始（注意并不是先访问根节点），中序遍历根节点的左子树，然后是访问根节点，最后中序遍历右子树

中序遍历算法：二叉树定义采用的递归形式，所以其遍历代码也可以采用递归，形式极其简单

void InOrderTraverse(BTNode* root)

	if(root==NULL)
		return NULL;
	InOrderTraverse(BTNode->lchild);//中序遍历左子树
	printf("%c",root->data);//结点访问操作，也可以是其他
	InOrderTraverse(BTNode->rchild);//中序遍历右子树
	

接下来，我们用下面的树来说明上述代码是怎样执行的

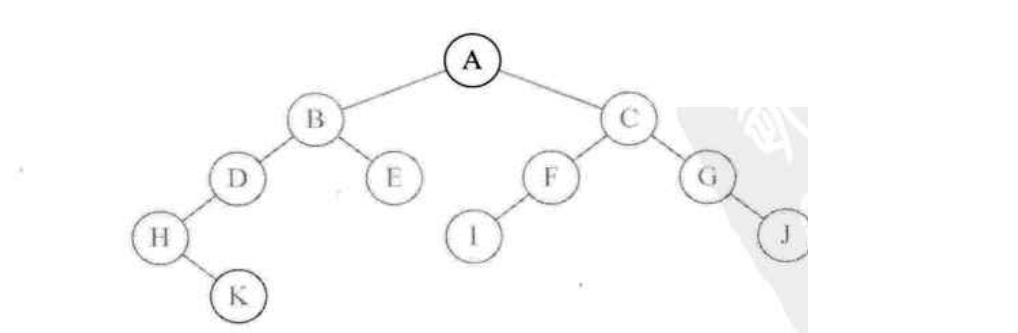
• 1：首先调用InOrderTraverse(A)，结点A不为空，于是再调用InOrderTraverse(A->lchild)，对于B来说也不空，于是再调用InOrderTraverse(B->lchild)，对于D来说也不空，于是再调用InOrderTraverse(D->lchild)。对于结点H，当其调用InOrderTraverse(H->lchild)时，由于其左孩子为空，因此会返回NULL，然后执行了printf，字母H被打印
  

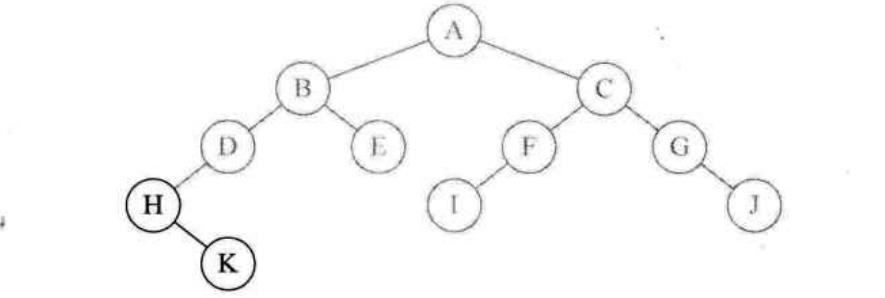
• 2：然后调用InOrderTraverse(H->rchild)，访问H的右孩子K，然后执行InOrderTraverse(K->lchild)，但其左孩子为空所以返回NULL，然后执行了printf，字母K被打印
  

• 3：然后InOrderTraverse(K->rchild)，但K没有右孩子，所以这直接导致InOrderTraverse(H->rchild)的结束，接着导致了InOrderTraverse(D->lchild)，然后执行了printf，字母D被打印
  

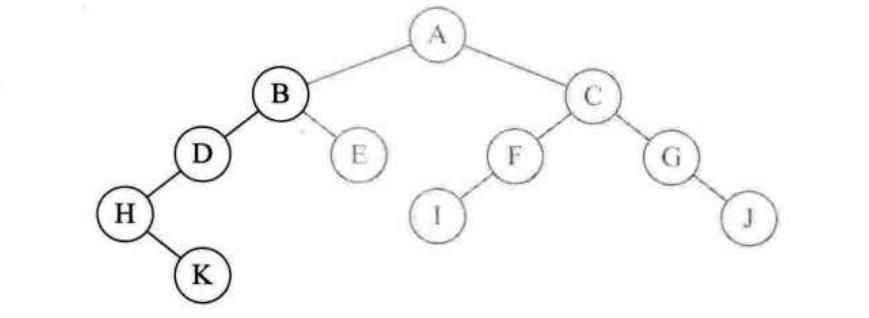
• 4：然后调用InOrderTraverse(D->rchild)，但D没有右孩子所以返回NULL，这直接导致了InOrderTraverse(B->lchild)的结束，然后执行了printf，字母B被打印
  

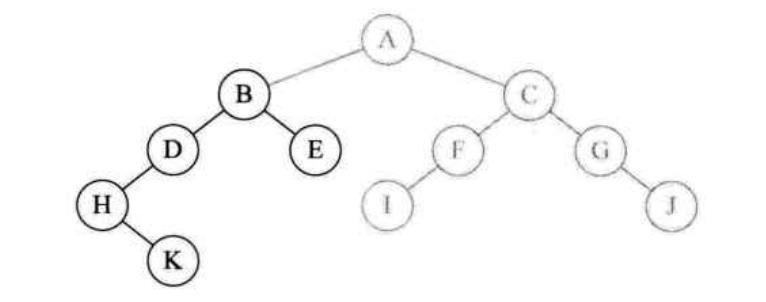
• 5：然后调用InOrderTraverse(B->rchild)，接着再调用InOrderTraverse(E->lchild)，但E没有左孩子所以返回NULL，然后执行了printf，字母E被打印
  

• 6：然后调用InOrderTraverse(E->rchild)，但E没有右孩子所以返回NULL，这就导致了InOrderTraverse(B->rchild)的结束，继而导致了InOrderTraverse(A->lchild)的结束，然后执行了printf，字母A被打印
  

• 7：然后调用InOrderTraverse(A->rchild)，开始A的右子树的遍历过程

• 8：后续访问过程不再赘述。遍历结果为$H-K-D-B-E-A-I-F-C-G-J$

（3）后序遍历-左右根(LRN)

后序遍历：前两次遇见结点不访问，最后一次遇见时访问

• 也即：若树为空，则返回空。否则从左到右先叶子后结点的方式遍历访问左右子树，最后根节点

后序遍历算法：二叉树定义采用的递归形式，所以其遍历代码也可以采用递归，形式极其简单

void PostnOrderTraverse(BTNode* root)

	if(root==NULL)
		return NULL;
	PostOrderTraverse(BTNode->lchild);//后序遍历左子树
	InOrderTraverse(BTNode->rchild);//后序遍历右子树
	printf("%c",root->data);//结点访问操作，也可以是其他
	

后序遍历大家可以自己推导一下

• 结果为：$K-H-D-E-B-I-F-J-G-C-A$

总结：三种遍历方式动图演示

本人学习数据结构时，对于三个地方理解的不是特别深入，其中有一个便是二叉树的递归，就如空中楼阁一般，感觉明白了，其实没有明白，这种感觉相信大家深有体会，的确不好受。不过在接触了很多和递归算法相关的题目及案例后，对于其理解确实有了一定的进步

所以我相信对于很多人来说，递归这一部分的理解也不是很到位（除大佬外），而天勤相较于王道来说，对于递归这一部分讲解确实很不错，人家把递归一层层的为我们剖析开来了。下面的图取自其视频课，质量不高（因为图片有大小限制），但是确实是一帧一帧的录制的，希望可以能大家的理解有所帮助

先序遍历

中序遍历

后序遍历

三：二叉树的层序遍历

层次遍历：需要借助队列完成。若树为空，则返回空，然后从上至下，从左至右依次访问结点

• 初始化一个辅助队列
• 根结点入队
• 若队列非空，则队头结点出队，访问该结点，然后将其左、右孩子（如果有）插入队尾
• 重复第三步，直至队列为空

具体过程如下图

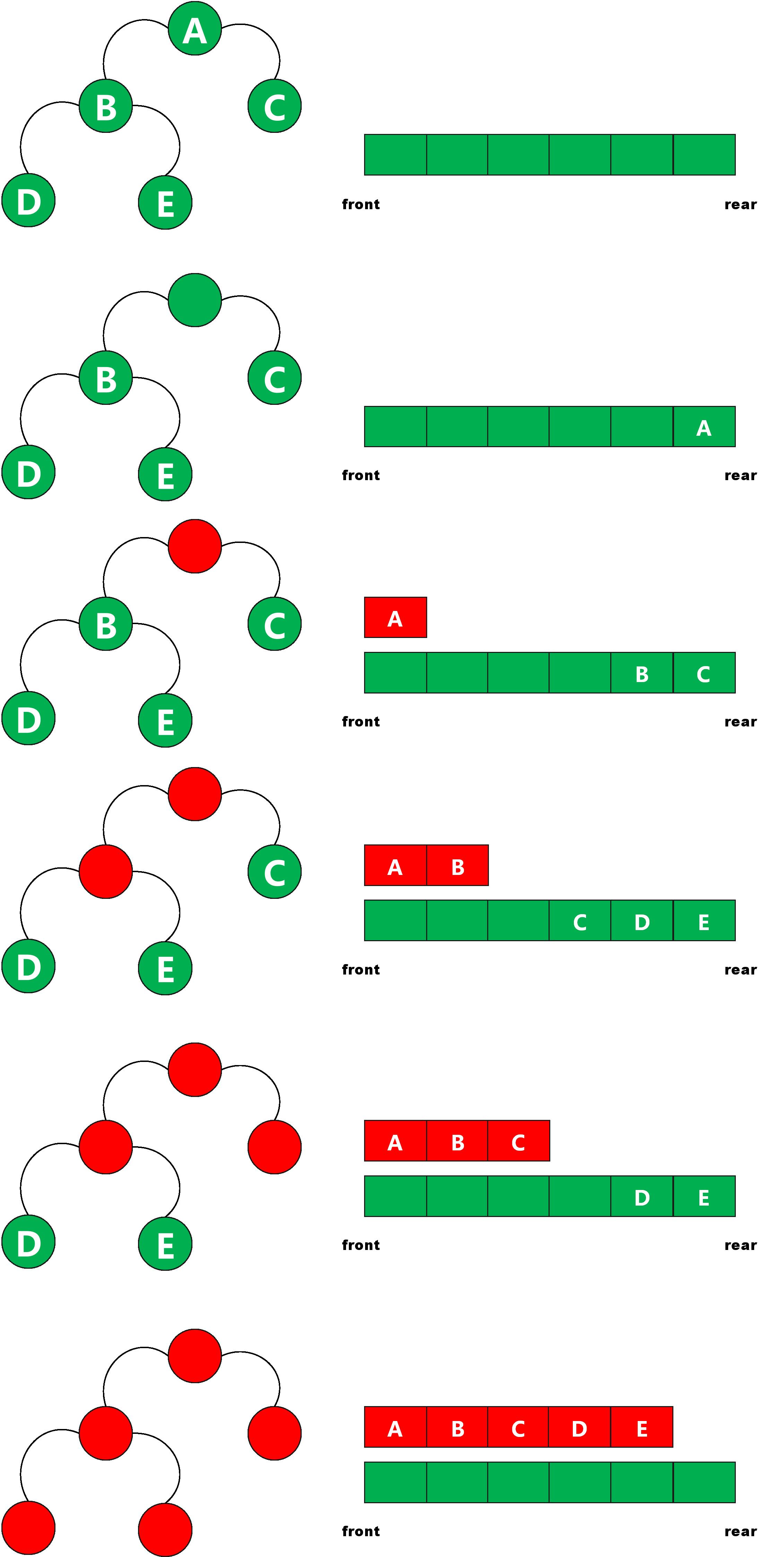
代码如下

void LevelOrder(BTNode* root)

	LinkQueue Q;
	InitQueue(Q);
	BTNode* p;//辅助结点
	EnQueue(Q,root);//先将根节点入队列
	while(isEmpty(Q))
	
		DeQueue(Q,p);//出队列，p拿到结点
		visit(p);
		if(p->lchild!=NULL)
			DeQueue(Q,p->lchild);
		if(p->rchild!=NULL)
			DeQueue(Q,p->rchild);