Python 大白从零开始 OpenCV 学习课-5. 图像的几何变换
Posted Python小白进阶
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Python 大白从零开始 OpenCV 学习课-5. 图像的几何变换相关的知识,希望对你有一定的参考价值。
从零开始 OpenCV 学习课-5. 图像的几何变换
本系列面向 Python 小白,从零开始实战解说 OpenCV 项目实战。
几何变换是指对图像的位置、大小、形状、投影进行变换,是将图像从原始平面投影到新的视平面。OpenCV 中的图像以多维数组描述,几何变换本质上是将一个多维数组通过映射关系求得另一个多维数组。
本节介绍图像的几何变换,提供完整例程和运行结果:位置变换:平移,旋转,镜像;形状变换:缩放,扭变;投影变换:透视投影,平行投影;极坐标变换。
1. 几何变换简介
几何变换是指对对图像的位置、大小、形状、投影进行变换,是将图像从原始平面投影到新的视平面。OpenCV 中的图像以多维数组描述,几何变换本质上是将一个多维数组通过映射关系求得另一个多维数组。
几何变换可以分为等距变换、相似变换、仿射变换和投影变换。在很多书籍中把等距变换、相似变换都称为仿射变换,常见的仿射变换包括平移、旋转、缩放、翻转、斜切等方法。
- 等距变换:图像中的长度、面积不变,典型的等距变换是 平移、旋转。
- 相似变换:图像中的长度比、夹角、虚圆点不变,相似变换是在等距变换的基础上进行了缩放,典型的相似变换是 缩放。
- 仿射变换:图像中的平行关系、面积比、共线线段或平行线段的长度比、矢量的线性组合不变,仿射变换是旋转和非均匀缩放的复合,典型的仿射变换是 斜切。
- 投影变换:图像中的共点、共线、相交、相切、拐点的关系不变,,投影变换是在仿射变换基础上进行的非线性缩放,典型的投影变换是 透视。

1.1 仿射变换
仿射变换(affine)的特点是原始图像中的平行关系和线段长度比例关系保持不变。
OpenCV 中的图像以多维数组描述,通过仿射变换变换为另一个多维数组(转换图像)。
仿射变换中的校正图像在二维空间中完成,在几何上定义为一个线性变换接一个平移变换。
仿射变换由以下公式描述:
[
x
~
y
~
1
]
=
M
A
[
x
y
1
]
,
M
A
=
[
a
11
a
12
a
13
a
21
a
22
a
23
0
0
1
]
\\begin{bmatrix} \\tilde{x}\\\\ \\tilde{y}\\\\ 1 \\end{bmatrix} = M_A \\begin{bmatrix} x\\\\ y\\\\ 1 \\end{bmatrix} ,\\hspace{1em} M_A= \\begin{bmatrix} a_{11} &a_{12} &a_{13}\\\\ a_{21} &a_{22} &a_{23}\\\\ 0 &0 &1 \\end{bmatrix}
⎣⎡x~y~1⎦⎤=MA⎣⎡xy1⎦⎤,MA=⎣⎡a11a210a12a220a13a231⎦⎤
OpenCV 提供了 cv2.warpAffine 函数实现仿射变换的操作。
仿射变换矩阵 MA 中有 6 个未知参数,cv2.getAffineTransform 根据图像中不共线的 3 个点在变换前后的对应位置坐标,构造 6元一次方程组即可求出仿射变换矩阵 MA。cv2.warpAffine 再用变换矩阵 MA 计算得到变换后的图像。
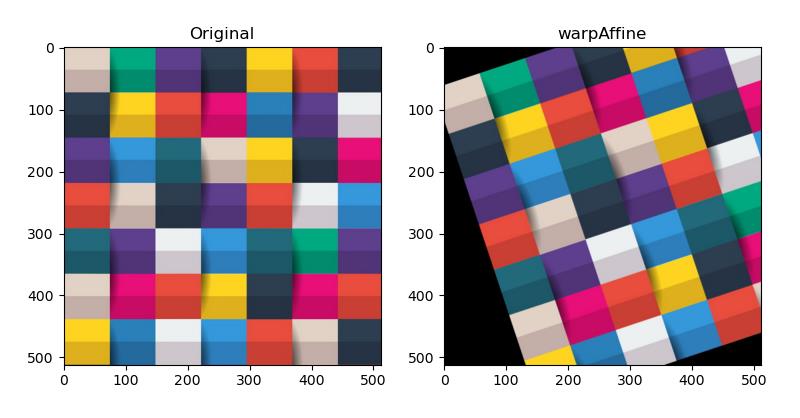
基本例程:1.33 图像的仿射变换
# 1.33 仿射变换: 平移、镜像、旋转 (cv2.warpAffine)
img = cv2.imread("../images/imgB2.jpg") # 读取彩色图像(BGR)
rows, cols, ch = img.shape
pts1 = np.float32([[50, 50], [200, 50], [50, 200]]) # 初始位置
pts2 = np.float32([[50, 100], [200, 50], [100, 250]]) # 终止位置
MA = cv2.getAffineTransform(pts1, pts2) # 计算 2x3 变换矩阵 MA
dst = cv2.warpAffine(img, MA, (cols, rows)) # 实现仿射变换
plt.figure(figsize=(9,6))
plt.subplot(121), plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB)), plt.title("Original")
plt.subplot(122), plt.imshow(cv2.cvtColor(dst, cv2.COLOR_BGR2RGB)), plt.title("warpAffine")
plt.show()
1.2 投影变换
投影变换(Projective mapping)也称透视变换(Perspective transformation),其特点是:原始图像中的平行关系、比例关系在转换后可以改变,但直线在转换后仍然保持直线。
投影变换将图片投影到一个新的视平面(Viewing plane),可以对三维空间中的物体旋转进行校正,主要用于图像拼接和校正透视投影导致的图像失真 。

投影变换由以下公式描述:
[
x
~
y
~
z
~
]
=
M
[
x
y
z
]
,
M
=
[
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
]
\\begin{bmatrix} \\tilde{x}\\\\ \\tilde{y}\\\\ \\tilde{z} \\end{bmatrix} = M \\begin{bmatrix} x\\\\ y\\\\ z \\end{bmatrix} ,\\hspace{1em} M= \\begin{bmatrix} a_{11} &a_{12} &a_{13}\\\\ a_{21} &a_{22} &a_{23}\\\\ a_{31} &a_{32} &a_{33} \\end{bmatrix}
⎣⎡x~y~z~⎦⎤=M⎣⎡xyz⎦⎤,M=⎣⎡a11a21a31a12a22a32a13a23a33⎦⎤
OpenCV 提供了 cv2.warpPerspective 函数实现投影变换的操作。cv2.getPerspectiveTransform 根据图像中不共线的 4 个点在变换前后的对应位置求得 (3x3) 变换矩阵,cv2.warpPerspective 使用该 (3x3) 变换矩阵即可求出变换后的图像。
1.3 极坐标变换
极坐标变换可以校正图像中的圆形物体和圆环中所包含的物体。
极坐标变换由以下公式描述:
KaTeX parse error: No such environment: align* at position 8: \\begin{̲a̲l̲i̲g̲n̲*̲}̲ r &= \\sqrt{(x-…
OpenCV 提供了 cv2.cartToPolar 函数和 cv2.ploarToCart 函数实现笛卡尔坐标与极坐标的相互转换。
2. 图像的平移
平移是物体位置在水平和垂直方向的移动。
像素点 (x,y) 沿 x 轴平移 dx、沿 y 轴平移 dy,可以由以下公式描述:
[
x
~
y
~
1
]
=
M
A
T
[
x
y
1
]
,
M
A
T
=
[
1
0
d
x
0
1
d
y
0
0
1
]
\\begin{bmatrix} \\tilde{x}\\\\ \\tilde{y}\\\\ 1 \\end{bmatrix} = M_{AT} \\begin{bmatrix} x\\\\ y\\\\ 1 \\end{bmatrix} ,\\hspace{1em} M_{AT} = \\begin{bmatrix} 1 &0 &d_x\\\\ 0 &1 &d_y\\\\ 0 &0 &1 \\end{bmatrix}
⎣⎡x~y~1⎦⎤=MAT⎣⎡xy1⎦⎤,MAT=⎣⎡100010dxdy1⎦⎤
由偏移量 (Tx, Ty) 按上式构造平移变换矩阵 MAT,由函数 cv2.warpAffine 可以计算变换后的平移图像。
函数说明:
以上是关于Python 大白从零开始 OpenCV 学习课-5. 图像的几何变换的主要内容,如果未能解决你的问题,请参考以下文章
Python 大白从零开始 OpenCV 学习课-1.安装与环境配置
Python 大白从零开始 OpenCV 学习课-5. 图像的几何变换
Python 大白从零开始 OpenCV 学习课-3.图像的创建与修改
Python 大白从零开始 OpenCV 学习课-4.图像的叠加与混合