L1正则化和L2正则化(从解空间角度)
Posted 卖山楂啦prss
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了L1正则化和L2正则化(从解空间角度)相关的知识,希望对你有一定的参考价值。
文章目录
一、什么是过拟合?
过拟合(overfitting)——就是学习器把训练样本学得“太好了”,以至于对测试样本“不知所措”。更形象的说就是,考试之前把模拟卷翻来覆去做,模拟题倒是做得非常好,结果考试拉胯了~拐求
欠拟合(underfitting)则刚好相反——学习器"hold不住"训练样本(模拟卷都做得不好,还考个屁式~)
来几张图片~图片来源:百度图片
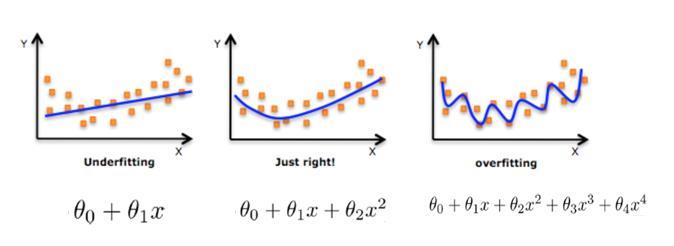
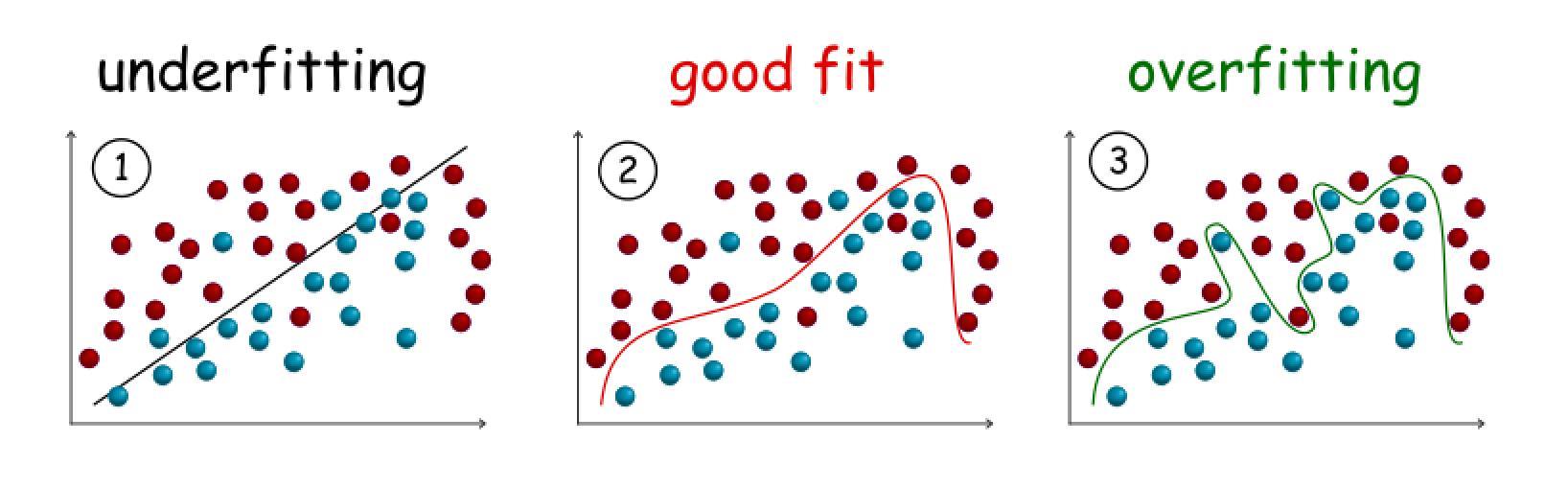
二、为什么模型会过拟合?
导致模型过拟合的情况有很多种原因,其中最为常见的情况是模型复杂度太高,导致模型学习到了训练数据的方方面面,学习到了一些细枝末节的规律。
即在统计模型中,由于使用的参数过多而导致模型对训练数据过度拟合,以至于用该模型来预测其他测试样本的时候,预测输出与实际输出或者期望值相差很大的现象。
比如在下面的图片中,参数逐渐增多,模型也变得越复杂,导致模型泛化能力下降,在后期应用过程中很容易输出错误的预测结果。
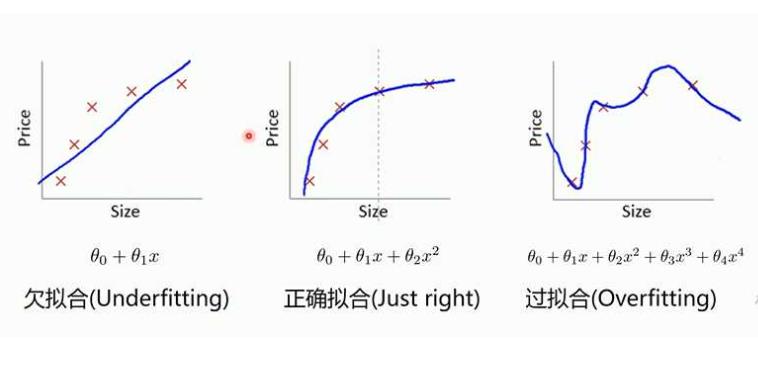
三、如何防止模型过拟合?
呐,如何防止过拟合?
引用《百面机器学习》,降低“过拟合”的方法
(1)从数据入手,获得更多的样本数据。比如可以通过一定的规则来扩充训练数据
(2)降低模型复杂度。例如,在神经网络模型中减少网络层数、神经元个数等;在决策树模型中降低树的深度、进行剪枝等。
(3)减少数据维度;降噪
(4)L1正则化和L2正则化方法,给模型的参数加上一定的正则约束。
(5)集成学习方法。集成学习是把多个模型集成在一起,来降低单一模型的过拟合风险,如Bagging方法。
上面的几种方法, L1正则化和L2正则化是比较常用降低过拟合的方法
可以把正则化理解为对模型参数的一种约束,或者说对损失函数的惩罚
我们知道
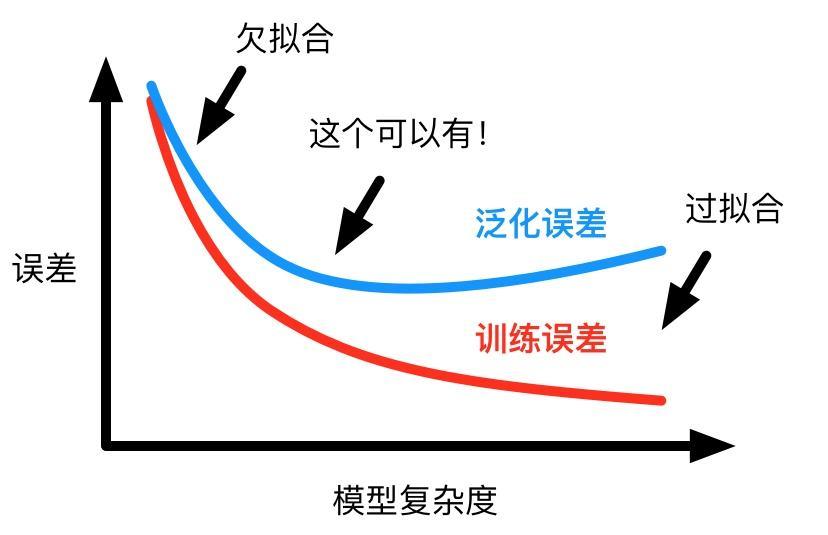
在机器学习中,模型误差 = 偏差 + 方差 + 不可避免的误差,而偏差和方差又是鱼和熊掌的关系,对模型中参数的惩罚力度越大,模型的复杂度越低,特征变化越简单,方差越小,即模型复杂度与模型方差呈正比关系。
==》解决过拟合的问题,也就是降低模型的方差。
==》模型正则化是减小方差,从而减小模型的泛化误差,而不是训练误差
四、L1正则和L2正则
前面提到:当使用的参数过多,模型复杂度太高==》会导致模型对训练数据过度拟合
因此,比较直接的就是,减少一些参数,不就可以避免过拟合了吗?问题是,怎么样让参数个数减少呐?==> 让一些参数等于0
L1正则化,就是可以让一些参数变为0,减少参数个数,相当于一个特征选择的过程,即可理解为抛弃掉一些不重要的特征,来降低模型的复杂度。
这里,让一些参数变为0 == 》L1正则化具有稀疏性
4.1 L1、L2的区别
可以把正则化理解为对模型参数的一种约束,或者说对损失函数的惩罚
- L1是模型各个参数的绝对值之和。
- L2是模型各个参数的平方和的开方值。
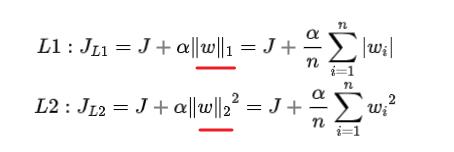
比如,在线性回归中,使用L1正则化的模型叫做Lasso回归
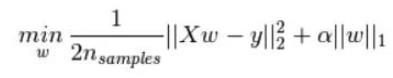
使用L2正则化的模型叫做Ridge回归(岭回归)
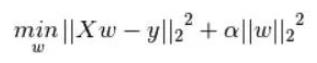
4.2 为什么正则化能够防止过拟合?
假设,我们的损失函数为均方误差MSE
J
=
∑
i
=
1
n
e
i
2
n
=
1
n
∑
i
=
1
n
(
y
i
−
y
^
i
)
2
=
1
n
∑
i
=
1
n
(
f
(
x
i
,
ω
i
)
−
y
^
i
)
2
J=\\frac{\\sum_{i=1}^n{e_{i}^{2}}}{n}=\\frac{1}{n}\\sum_{i=1}^n{\\left( y_i-\\hat{y}_i \\right) ^2}=\\frac{1}{n}\\sum_{i=1}^n{\\left( f\\left( x_i,\\omega _i \\right) -\\hat{y}_i \\right) ^2}
J=n∑i=1nei2=n1i=1∑n(yi−y^i)2=n1i=1∑n(f(xi,ωi)−y^i)2
我们的目标是使损失函数最小化
任意一组参数组合 ω 1 , w 2 , ⋯ , ω n \\omega _1,w_2,\\cdots ,\\omega _n ω1,w2,⋯,ωn 都可以得到一个损失值,并且可能有多组参数的结果为同一个损失值
假设以二维为例: ω 1 , w 2 \\omega _1,w_2 ω1,w2, J = ω 1 2 + ω 2 2 J=\\omega _{1}^{2}+\\omega _{2}^{2} J=ω12+ω22 的图形如下
有点像一个碗
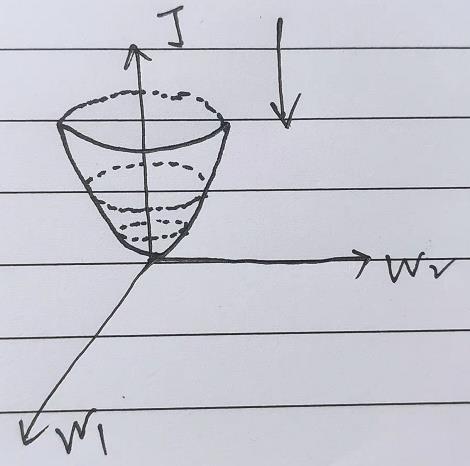
从上往下看,可以得到损失函数的等高线,最中间的即为损失值最小,同一个圈,任意一点,损失是一样的

或者,可以结合这个图,就好理解了

正则化即在损失函数后加入惩罚,如 L1泛数 ∥ ω ∥ 1 \\lVert \\omega \\rVert _1 ∥ω∥1
L 1 = J + α ∥ ω ∥ 1 = J + α ∑ i = 1 n ∣ ω 1 ∣ L1=J+\\alpha \\lVert \\omega \\rVert _1=J+\\alpha \\sum_{i=1}^n{\\left| \\omega _1 \\right|} L1=J+α∥ω∥1=J+αi=1∑n∣ω1∣
这种惩罚,也就是对参数进行了限制
二维为例,参数w被限制到一定的区域内,如下图

可以看成一个最优化问题
{
min
L
=
J
s
.
t
∣
ω
1
∣
+
∣
ω
2
∣
+
⋯
+
∣
ω
n
∣
≤
m
\\left\\{ \\begin{array}{l} \\min\\text{\\ }L=J\\\\ \\\\ s.t\\ \\left| \\omega _1 \\right|+\\left| \\omega _2 \\right|+\\cdots +\\left| \\omega _n \\right|\\le m\\\\ \\end{array} \\right.
⎩⎨⎧min L=Js.t ∣ω1∣+∣ω2∣+⋯+∣ωn∣≤m
或者
{ min L = J s . t ω 1 2 + ω 2 2 + ⋯ + ω n 2 ≤ m \\left\\{ \\begin{array}{l} \\min\\text{\\ }L=J\\\\ \\\\ s.t\\ \\omega _{1}^{2}+\\omega _{2}^{2}+\\cdots +\\omega _{n}^{2}\\le m\\\\ \\end{array} \\right. ⎩⎨⎧min L=Js.t ω12+ω22+⋯+ωn2≤m
不等式约束最优化问题==》KKT
KKT,假设最优化问题满足KKT条件,那么解空间必定满足一下这些公式

用到拉格朗日函数

因此,可以通过KKT公式,和拉格朗日求解法,求偏导得到未知数
4.3 为什么L1正则具有稀疏性或者说L1正则能够进行特征选择?
所谓稀疏性,说白了就是模型的很多参数是0
一般,数据特征数量很多,但是大部分特征可能对模型的预测都没有作用,甚至让模型变得很复杂,影响模型预测,
只有少数特征对这个模型有贡献,绝大部分特征是没有贡献的,即使去掉对模型也没有什么影响,此时我们就可以只关注系数是非零值的特征。
这相当于对模型进行了一次特征选择,只留下一些比较重要的特征,提高模型的泛化能力,降低过拟合的可能。
所以, 从解空间的形状角度来看
例子(二维)
目标损失函数为凸函数,其等高线如下,每一个圈相当于一个损失值,圈越小,损失值越小,也就是追求的损失函数最小化,最好就是得到最小圈的参数值(结合那个碗)

前面提到,二维的L1正则 ∣ ω 1 ∣ + ∣ ω 2 ∣ \\left| \\omega _1 \\right|+\\left| \\omega _2 \\right| ∣ω1∣+∣ω2∣ 或者L2正则 ω 1 2 + ω 2 2 \\omega _{1}^{2}+\\omega _{2}^{2} ω12+ω22 的图是这样
L1 ==》菱形
L2 ==》圆形
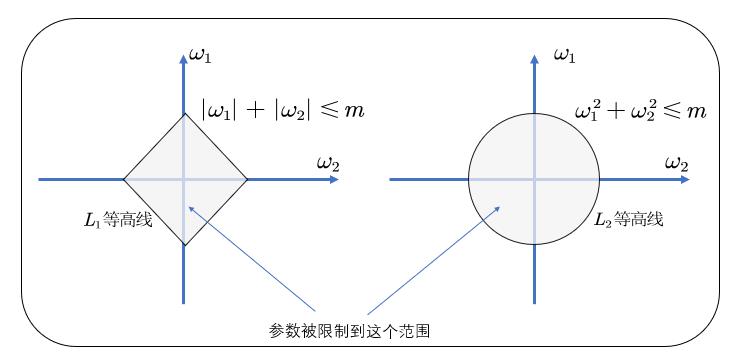
因为加入正则,不管是L1,还是L2,w1和w2的取值范围只能是这个圈圈内,或者边上
也就是参数被限制到这个区域内(本来是任意区域)
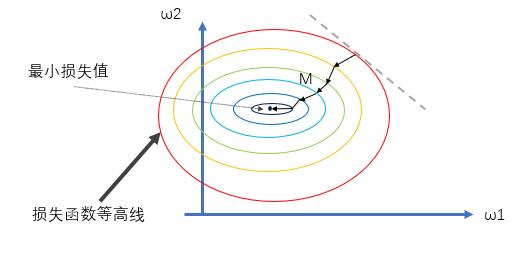
首先,来看一下不加正则的情况,使用梯度下降法去优化损失函数,随机选择一点,沿着梯度方向下降,得到一个近似的最优解M
接下来,加入正则
正则限制和损失最小分别代表两个优化问题,对原始的损失函数J添加了正则像之后,优化问题就变成了两个子优化问题的博弈。
二维情况下,L1正则的等高线因为是有棱有角的,所以更可能在顶点处与损失函数相交(概率更大),也有可能不在顶点,是在线上相切,或在其他位置,但是通常最优的参数值很大概率会出现在坐标轴上,这样就会导致某一维的权重为0 ,也就是使得其中一个参数w为0,比如这里第二种情况w2=0(相交点就是最优解),产生稀疏权重矩阵,这就是为什么L1正则化倾向于让模型得到一个稀疏解,即参数会有很多0。
(1)这是一种情况
只有一个交点,L1正则 在顶点上,L2正则 在切线上
两个相交点或相切点处既满足损失函数,又满足正则项的参数限制
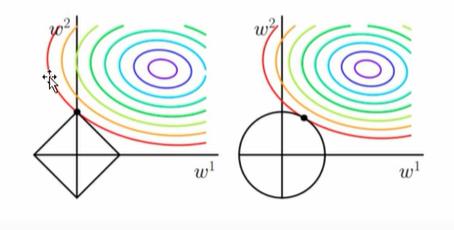
(2)这是另外一种情况
可以看到,在顶点处的参数组合,是损失值最低的,可以得到最优的参数组合是顶点处。
然后,扩展到多个参数,那么这个图形就更加有棱有角,相交的点大概率是顶点,使得参数为0

(3)或者这种情况
引自:https://zhuanlan.zhihu.com/p/113373391
的主要内容,如果未能解决你的问题,请参考以下文章</p>
<p > <a style=)