生存分析——KM生存曲线hazard比例PH假定检验非比例风险模型（分层/时变/参数模型）

Posted 悟乙己

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了生存分析——KM生存曲线hazard比例PH假定检验非比例风险模型（分层/时变/参数模型）相关的知识，希望对你有一定的参考价值。

文章目录

本系列学习笔记：

1 数据类型

1.1 删失数据

参考：生存分析的数据类型(左删失、右删失…)，你都了解吗？

生存分析的数据资料常常分为终点事件（如死亡）和删失（其他生存结局）两类

与完全数据相反，如果在研究结束的时候，研究对象发生了研究之外的其他事件或生存结局，无法明确的观察记录到发生终点事件的生存时间，我们把这种类型的数据称之为删失数据，或不完整数据（Incomplete data）。

产生删失的可能原因

  • (1) 到达研究截止日期时，终点事件仍然没有发生，研究对象依然存活
  • (2) 研究对象因为搬迁、更换电话号码等原因失去联系造成失访，无法明确观察到研究对象是否发生了终点事件，以及具体的发生时间
  • (3) 研究对象不配合、或医生改变治疗方案等其他原因，造成研究对象中途退出研究，无法继续进行随访观察
  • (4) 研究对象死于其他事件，例如死于交通事故，或者因其他疾病造成死亡

几种删失：

  • 右删失（Right censored）：起点已知，终点不确定（最常见）
  • 左删失（Left censored）：起点无法确定
  • 区间删失（Interval censored）：连续的观察随访中，已知发生终点事件，但起点未知

1.1.1 右删失

在进行随访观察中，研究对象观察的起始时间已知，但终点事件发生的时间未知，无法获取具体的生存时间，只知道生存时间大于观察时间，这种类型的生存时间称为右删失。
根据观察结束时间的不同，可以进一步分为3种类型：

  • I型删失（Type I censoring）：同起点，同时间终点
    所有研究对象的观察起点时间是统一的，在研究随访的过程中，除了已经发生终点事件的研究对象外，其余研究对象的观察时间统一截止到某一固定的时间，这种删失类型即为I型删失。I型删失的删失时间是固定的，因此又称为定时删失。I型删失不允许个体在研究的过程中退出。

  • II型删失（Type II censoring）：同起点，固定数量的终点
    所有研究对象的观察起点时间是统一的，在研究的过程中，一直随访观察到有足够数量的终点结局事件发生为止，此时研究停止，未发生终点事件的研究对象的生存时间未知，这种删失类型即为II型删失。II型删失可以理解为删失比例是事先已经设定的。

  • III型删失（Type III censoring）：不同起点，无固定终点
    在实际的研究过程中，往往不能保证所有研究对象在同一时间同时进入研究，在研究开始后，随着研究对象的陆续招募进入研究，不同研究对象的观察起始时间有先有后。同时，在研究结束前，有些研究对象已经发生终点事件，可以记录其准确的生存时间，但也有些研究对象中途退出研究，或者在研究结束时仍然未发生终点事件，他们的生存时间无法明确。这种观察起始时间和删失时间均不相同的类型，称之为III型删失，也是临床研究中最为常见的类型。由于删失数据往往是随机发生的，因此III型删失也称为随机删失（Random censoring）。

1.1.2 左删失

起点未知

假设研究对象在某一时刻开始进入研究接受观察，但是在该时间点之前，研究所感兴趣的时间点已经发生，但无法明确具体时间，这种类型即为左删失数据。

例如，某项关于脑卒中复发危险因素的研究，生存时间规定为从第一次脑卒中发病到下一次脑卒中发病之间的时间间隔。在研究起始时刻对研究对象进行问卷调查，询问是否发生过脑卒中，以及第一次脑卒中发病的时间，如果研究对象回答“发生过脑卒中，但不记得发病的具体时间了”，此时无法明确获取第一次脑卒中发病时间，该数据即为左删失。

1.1.3 区间删失

连续的观察随访，起点未知

在实际的研究中，如果不能够进行连续的观察随访，只能预先设定观察时间点，研究人员仅能知道每个研究对象在两次随访区间内是否发生终点事件，而不知道准确的发生时间，这种删失类型称为区间删失。

例如某个研究对象在第一次随访时间点未观察到终点事件发生，在下一次随访时已经发生了终点事件，但研究人员无法获取发生时间的具体时间，只知道在这两次随访间隔的中间，生存时间并不明确，因此则认为该研究对象的生存时间在两次随访间隔内是区间删失。

1.2 完全数据（Complete data）

在研究过程中，如果能够明确的观察记录到每个研究对象的生存时间，或发生终点事件的具体时间，我们把这种类型的数据称之为完全数据。其中生存时间（Survival time）是指从规定的观察起点（起始事件）到发生某一特定终点事件之间经历的时间跨度。

2 生存分析几个核心概念

有参考：
生存分析简明教程
生存分析：寿命表，Kaplan-Meier，Cox回归，时依协变量

生存分析要解决的核心问题就是各组样品数据在一个或者多个变量作用下它们生存概率随着观测时间如何发展（变化）以及它们之间的可比性。

2.1 生存概率

即 Survival probability，指的是研究对象从试验开始直到某个特定时间点仍然存活的概率，可见它是一个对时间t的函数，我们定义之为 S(t)；
表示观察对象生存时间越过时间点t的概率，t=0时生存函数取值为1，随时间延长生存函数逐渐减小。
以生存时间为横轴、生存函数为纵轴连成的曲线即为生存曲线。

Kaplan-Meier 方法主要关注 S(t)

2.2 风险概率

即 Hazard probability ，指的是研究对象从试验开始到某个特定时间 t 之前存活，但在 t 时间点发生观测事件如死亡的概率，它也是对时间 t 的函数，定义为 H(t)。

h(t)=f(t)/S(t)。其中f(t)为概率密度函数（Probability Density Function），f(t)是F(t)的导数。F(t)为积累分布函数（Cumulative Distribution Function），F(t)=1-S(t)，表示生存时间未超过时间点t的概率。累积风险函数H(t)=-logS(t)。

Cox 风险比例模型则关注 H(t)。

2.3 生存/风险函数 两者之间关系

两者必定有关联，但是之前大多数博客都没怎么理清两者之间的关系，
幸好这篇怎么理解生存分析的风险函数?有讲的非常透彻的，具体可见原文，来先看 风险函数 h(y) ~ 生存函数S(y) 之间的关系：

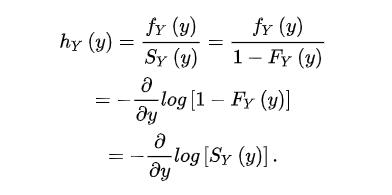
面式子中，第三个等号后的公式利用了密度函数和分布函数的转化关系

生存函数S(y)~风险函数 h(y) 关系：

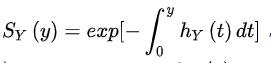
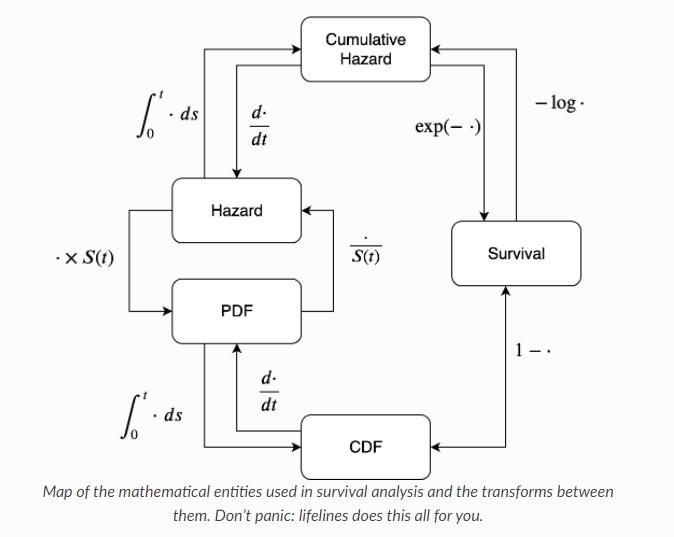
2.3 Ht / St / CDF / CF之间的关系

20210804更新，可参考：hazard-function
又看到一个比较好的介绍多者关系的：

  • 累积分布函数（CDF, Cumulative distribution function）
  • Hazard密度函数PDF：estimated density function
  • Ht 风险函数
  • Survival 生存函数

2.4 其他生存时间相关概念

参考：生存分析不止中位生存时间

  • 生存时间（Survival Time）：常用t表示，从规定的起始事件开始到失效事件出现所持续的时间。对于失访者，是失访前最后一次随访的时间。

  • 中位生存时间（Median Survival Time）/平均生存时间（Mean Survival Time）：中位生存时间又称半数生存期，表示恰好一半个体未发生失效事件的时间，生存曲线上纵轴50%对应的时间。平均生存时间则表示生存曲线下的面积。

  • 第p百分位生存时间[pth Quantile Survival Time]
    与中位生存时间相似，第p百分位生存时间描述(时所对应的生存时间。

  • 限制性平均生存时间[Restricted Mean Survival Time, RMST]
    描述受试人群在随访 t t t 时间段内的平均生存时间，一般利用 t t t 时间段内生存曲线下面积或累计发病率曲线上面积表示。其与平均生存时间的区别在于限制性平均生存时间事先规定了随访时间 t t t 。限制性平均生存时间是医学研究中有用的指标之一

  • 平均剩余寿命[Residual Mean Life Time, mrl]
    描述受试人群在活过时间 [公式] 后的平均剩余生存时间。通常，平均剩余寿命多用于删失受试者中。其计算公式为，

3 Kaplan-Meier 生存概率估计

感觉这篇里面讲的清楚些：生存分析简明教程

3.1 寿命表（ life table）

  • A 列是从试验开始起，持续的观测时间，星号代表在该时间有删失数据发生；
  • B 列是指在 A 列对应的时间开始之前所有存活的研究对象个数，也可以叫做 at risk 的人数，表示当前具有死亡风险的有效人群，是排除了已经死亡和删失的数据之后剩余的人数；
  • C 列为恰好在 A 列对应的时间死亡的人数，
  • D 列即表明在该时间点删失的个数。

第一行则可以解读为，在 0.909 年这个时间点之前，本来有 10 个患者，在 0.909 这个时间点（或其之后的一小段时间区间）死亡了一个人，没有删失数据，意味着还剩 9 人；随后，只要有新增死亡或删失数据，则在表中新建一行，记录时间和人数。

3.2 Kaplan–Meier 方法

Kaplan–Meier 方法的主要思路，基于刚才的表格，我们也可以用数学公式来表示。一共有 m 个时间点，每个时间点用下标 i 来表示, i 为从 1 到 m 的整数, 生存概率 S(ti) 可以表示为：

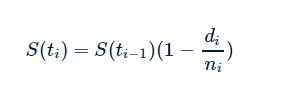
其中，ti 表示第 i 个时间点，ni 表示在 ti 之前的有效人数，di 表示在 ti 死亡的人数，S(ti-1) 表示在上一个时间点 i-1 的生存概率。

如何计算每个时间节点的生存概率，即 S(t)。
比如在 1.536 年这个时间点，即表中的第五行，病人在该点的生存概率是多少呢？
很容易可以想到，要想在 1.536 这个时间点存活，他/她必须在 1.536 之前的所有时间点存活才行，也就是说在 0.909、1.112、1.322、1.328 这几个时间点，病人都必须存活。
那么在 1.536 这个时间点的生存概率 P 实际上就等于在包括 1.536 在内的所有之前的时间点都不死亡的概率乘积，即：

P(存活至1.536) = P(0.909时不死亡) * P(1.112时不死亡) * P(1.322时不死亡) * P(1.328时不死亡) * P(1.536时不死亡)

当我们计算出每个时间点不死亡的概率之后，我们就可以通过连续乘积算出每个时间点的生存概率，即存活至该时间点的概率。如下表所示：

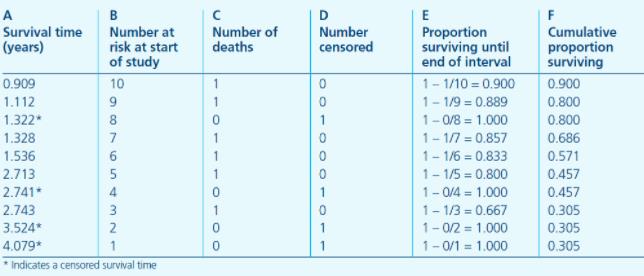
该表中 E 列即不死亡概率，F 列则表示累积的生存概率，可以看到随着时间增加，死亡人数增多，越到后期，生存概率越低，这是符合常理的。另外需要注意，在删失发生时，生存概率时没有变化的。

画图来展示生存率的变化情况，即 Kaplan-Meier 生存曲线，如下图所示：

图中横轴即时间轴，纵轴是累积存活比例，也就是生存概率，加号表示删失数据。
一般来说，生存分析是要比较不同组之间的一个生存情况，因此 Kaplan-Meier 生存曲线一般不止一条曲线，如下图所示：

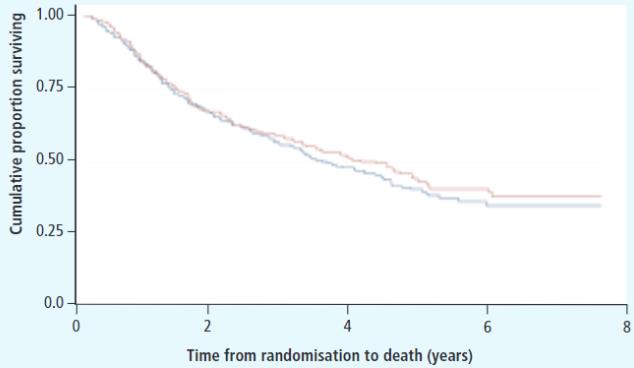
图中不同颜色表示不同的两组病人，在时间轴上生存情况的不同表现。该图中，红色和蓝色的线基本上重叠在一起，后期红色线稍微高一点，也就是说红色组的后期生存概率更高，病人死亡的相对慢一点。可以想象，如果某一组的生存情况特别差，那么它的生存曲线应该是一条极速下降的阶梯状。

3.3 KM组别差异的指标一：中位生存时间

生存率在 50% 时所对应的生存时间，如下图所示：

不同组别对应的中位生存时间不同，可以一定程度上反应出不同组别死亡风险的不同。

3.4 KM组别差异的指标二：Logrank /Breslow

整体生存时间分布是否存在统计学差异，一般我们可以采用 Logrank 统计方法来对生存数据进行统计分析。

Logrank 方法是由 Nathan Mantel 最初提出的，它是一种非参数检验，中文翻译为对数秩检验，主要用来比较两组样本的生存时间分布的差异。

Logrank 检验的零假设是指两组的生存时间分布完全一致

当我们通过计算拒绝零假设时，就可以认为两组的生存时间分布存在统计学差异。

除 Logrank 检验之外，一种生存时间分布的常用检验包括 Breslow 检验，其实也就是 Wilcoxon 检验，与 Logrank 不同的是，在每个时间点统计观测人数和期望人数时，他会给它们乘以一个权重因子，即当前时间点的 at risk 的总人数，然后再把所有时间点加起来去统计卡方值。

可以想象随着时间点越靠后，at risk 的总人数会越小，因此权重越少，对 X2 值的贡献就越小。

因此 Breslow 检验对试验前期的差异要更加敏感，而相对来说 Logrank 对后期相对更敏感一些，因为它的所有时间点的权重参数都是1.
在实际使用中，我们可以使用不同的方法从多个角度对数据去进行探究。

4 Cox 比例风险回归模型

生存分析简明教程
生存分析：寿命表，Kaplan-Meier，Cox回归，时依协变量

4.1 cox比例风险模型公式

Cox 模型是一种半参数模型，因为它的公式中既包括参数模型又包括非参数模型。简单说下参数模型和非参数模型的相同与区别。

其中 t 是生存时间，x1, x2 到 xp 指的是具有预测效应的多个变量，
b1, b2 到 bp 则是每个变量对应的 effect size 即效应量，可以理解为结果的影响程度，后面会解释。
h(t) 就是不同时间 t 的 hazard，即风险值。
而 h0(t) 是基准风险函数，也就是说在其他协变量 x1, x2, …, xp 都为 0 时，即不起作用时，衡量风险值的函数。
根据公式我们可以看到指数部分是参数模型，因为其参数个数有限，即b1, b2 到 bp，而基准风险函数 h0(t) 由于其未确定性，可根据不同数据来使用不同的分布模型，因此是非参数模型。
所以说, Cox 模型是一种半参数模型。

4.2 （重要）如何检验：比例风险假定（PH 假定）

参考：教你三招：Cox回归比例风险(PH)假定的检验

并不是所有的生存分析数据都可以用 Cox 模型来分析，它是需要满足一定的假设的：比例风险假定

风险比(hazard ratio)  =>  exp(协变量系数)
比例风险假定（PH 假定，proportional-hazards assumption） =>  与h0(t)无关，风险比为固定值 =>  协变量回归系数是固定的

4.2.1 接分组看KM生存曲线

两条生存曲线最后交叉，这说明PH条件不成立。
（需说明的是，曲线不交叉不代表PH条件一定成立）

举例：
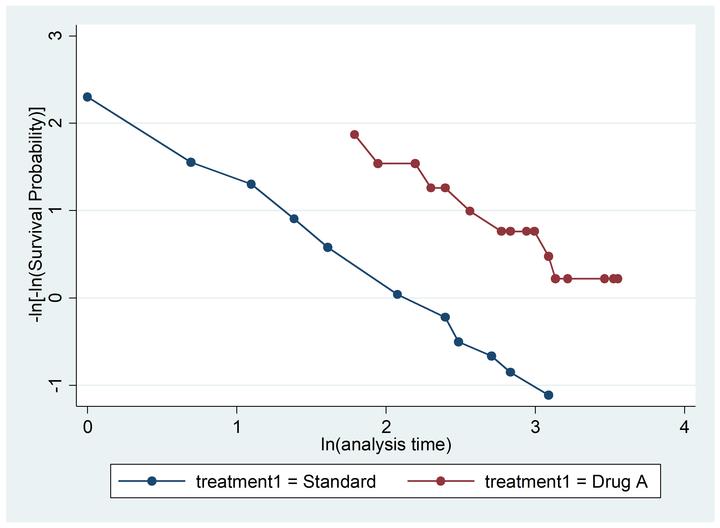从图中可以看出，Treatment1代表的两种治疗方法，曲线基本平行，因此可认为该变量的PH假定基本成立。
另外一个：

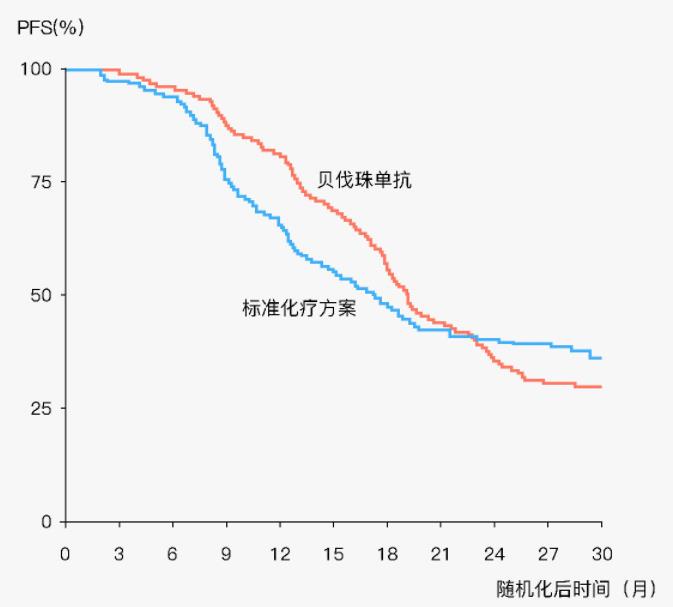
两条生存曲线最后交叉，这说明PH条件不成立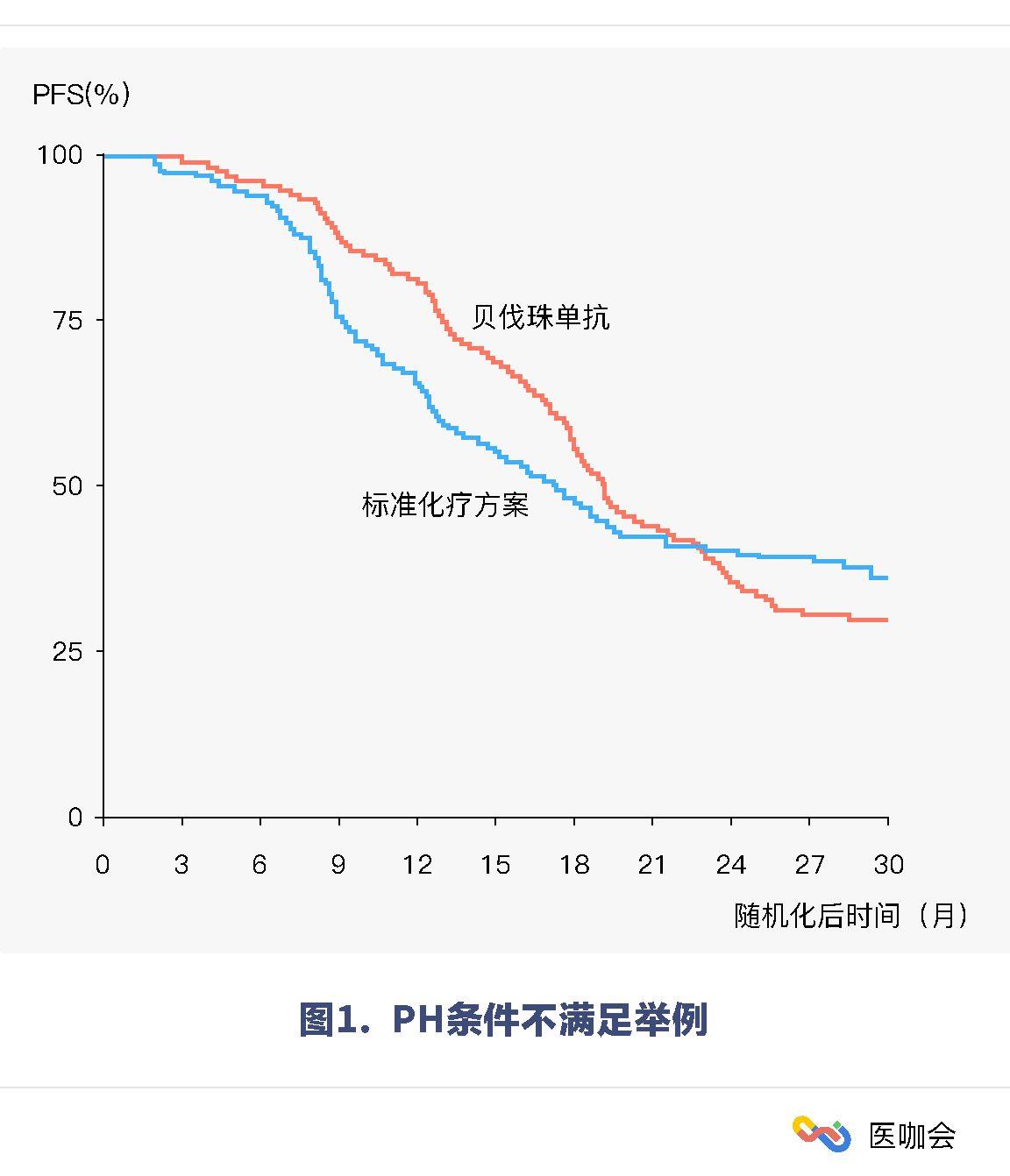

4.2.2 预测生存概率图法

判断标准：利用拟合的Cox回归方程生成概率曲线，该曲线假定PH成立，然后与实际得到KM曲线做比较，如果两条曲线基本重合说明PH假定成立。

判断：图中Observed曲线为根据实际数据得到的K-M曲线，Predicted曲线为假定PH成立的Cox模型拟合出的曲线，可以看到，在两个治疗组中，曲线基本重合，因此说明PH假定是成立的。

4.2.3 proportional_hazard_test 统计检验法

判断标准：该法将给出统计学检验的P值，通过P值判断。
P值越小，说明系数随时变效果越明显，p值<0.05 则没有通过假定,协变量相对于基线随时间变化的影响

以下是stata的输出结果：
教你三招：Cox回归比例风险(PH)假定的检验

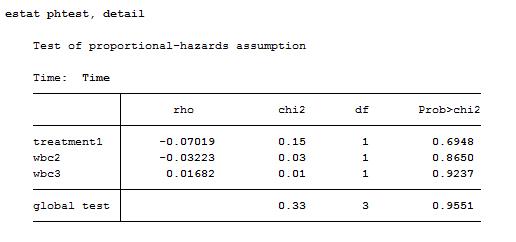
前三行给出的是纳入Cox模型的三个变量各自的检验结果，可以看到P值均不显著，因此不能认为违反PH假定。
最后一行给出的模型整体性的PH检验结果，同样不能认为违反PH假定。

这是python的lifelines包输出的，可参考教程：Testing the proportional hazard assumptions

cph.check_assumptions(rossi, p_value_threshold=0.05, show_plots=True)

结果一，变量检验表：

结果二：直接指出哪些变量有问题

1. Variable 'age' failed the non-proportional test: p-value is 0.0007.

   Advice 1: the functional form of the variable 'age' might be incorrect. That is, there may be
non-linear terms missing. The proportional hazard test used is very sensitive to incorrect
functional forms. See documentation in link [D] below on how to specify a functional form.

   Advice 2: try binning the variable 'age' using pd.cut, and then specify it in `strata=['age',
...]` in the call in `.fit`. See documentation in link [B] below.

   Advice 3: try adding an interaction term with your time variable. See documentation in link [C]
below.

4.2.4 Schoenfeld 残差图

Time-Dependent 生存模型分析用户流失

这是用R的survival包来画的：

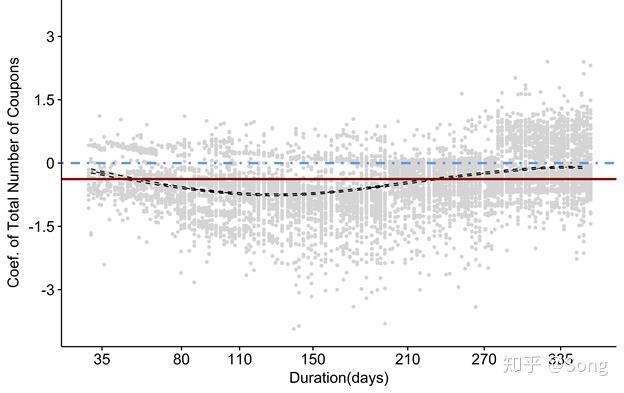
其中黑色曲线为影响系数随时间的变化拟合曲线，而棕色则是传统的比例COX模型的拟合结果。
可见随时间变化明显，不能采用简单的比例COX模型建模。

这是python的lifelines包画的，可参考教程：Testing the proportional hazard assumptions

4.3 比例风险COX回归如何解读结果

4.3.1 常规解读

假设我们已经通过计算得到了合适的 h0(t) 和协变量系数，如何去解读结果呢？
我们可以比较某个协变量 x1 在不同值时对应的不同风险比(hazard ratio)，这里比较 x1 和 x1+1，即若 x1 增加 1 个单位，增加前后的风险比是：

那么比例风险假定的解读就有以下几点：

  • 该比值与h0(t)无关，在时间上为常数，即模型中协变量效应不随时间变化而改变
  • 不论基准风险如何，在任何时间点上存在某一暴露的个体相对不存在该暴露的个体发生事件的风险是恒定的
  • 两组人群在任何时间点上发生事件的风险比例是恒定的
  • 解释为某一暴露在所有时间里对发生事件的作用都是相同的

上式中，我们对 x1+1 和 x1 这两个不同的值对应的风险比进行了计算，通过化简可知x1+1 和 x1 对应的风险比实际上等于 exp(b1)
假如

  • x1 指的是年龄，那么对于年龄 51岁 (x+1) 和年龄 50 岁 (x) 的人，可能死亡的风险比为 exp(b1)。
  • 如果 b1>0，则 exp(b1)>1，意味着年龄 +1，死亡风险增加；
  • 如果 b1<0, 则 exp(b1)<1，意味着年龄 +1，死亡风险降低；
  • 如果 b1=0，exp(b1)=1，意味着年龄变化对死亡风险不起作用。

对于每一个协变量，如果它的系数为正，表明对应的变量增加时，会增加病人的死亡风险（或其他事件风险，如复发、转移等）；
如果它的系数为负，表明对应的变量值增加时，会降低病人的死亡风险。

再来看具体的回归结果如何解读：

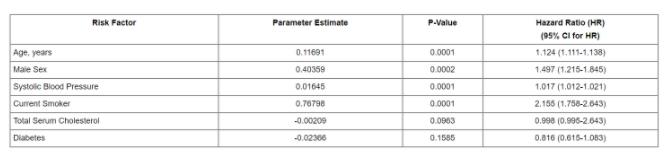
一些风险因子包括年龄、性别、血压（收缩压）、是否抽烟、血清总胆固醇以及是否患有糖尿病，经过 Cox 模型计算，得到各个风险因子的参数估计，如年龄对应的参数为 0.11691，也就是之前公式中的系数为 0.11691，大于 0 表示年龄增加会增加风险，风险比 (hazard ratio) 为 exp(0.11691) = 1.124 ，即表格最后一列，该数值大于 1，同样表明年龄增加会导致风险增加。

对于二分类变量，即只有 0 和 1，比如男性为 1，女性为 0，这样的变量与连续变量在 Cox 模型中的结果解读是一致的，如果性别对应的协变量系数大于 0，表明性别值越高风险越大，也就是说男性的风险高与女性。

除了关注系数外，同时需要关注的是 p value，即该参数估计是否具有统计学显著性，常用来统计的方法是 Likelihood ratio test，同时也有使用 Wald test, 和 score logrank statistics。

可以作为特征选择的方式
简单介绍一下 Likelihood ratio test，中文名叫似然比检验，
核心思想是：为了判断都某个新变量的引入是否对于模型有效，比较变量加入前和加入后，似然函数最大值的比较，如果没有出现最大值的降低，那么则可能对模型有效，进而统计其显著性。

4.3.2 解读二：用户流失的生存模型分析

参考：Time-Dependent 生存模型分析用户流失

最终的COX模型结果输出都是类似的，主要需要看三列，第一列为系数，如果为正，则表示会增大风险，为负则减小风险。第二列为比值，即使风险（hazard rate）系数增大或减小的倍数，最后则是看P值，表示是否显著（这个解释和对logit model做解释很像，hazard rate类似于odds ratio，都是对系数做exp）。
举个例子，下图为一个原始的COX模型结果，可见优惠券的数量（total_number）可以明显的降低用户流失风险，且每增加一个优惠券，风险会变为原来的0.94倍。

5 非比例风险模型

生存分析：寿命表，Kaplan-Meier，Cox回归，时依协变量

Cox回归最重要的前提条件是假定风险比为固定值，当PH不满足时，可以采用的几种方法：

  • 分层变量，可将不呈比例关系的协变量作为分层变量，然后再将剩余变量进行Cox回归分析；
  • 时变协变量，第二种方法是采用时依协变量进行分段Cox回归；
  • 第三种方法是采用参数回归模型替代Cox回归模型

5.1 分层变量

层（Strata）：
分层变量，用于分层分析，控制混杂因素。
若选入变量，结果将按该变量的各水平分别输出。

有一些SPSS的教程比较好：
非比例风险的Cox回归模型_分段模型
生存分析：寿命表，Kaplan-Meier，Cox回归，时依协变量

5.2 时变协变量

非比例风险的Cox回归模型_时依系数法
Time-Dependent 生存模型分析用户流失

5.2.1 时依协变量 类型

时依协变量（Time-Dependent Covariate），所谓时依协变量，顾名思义指的就是随时间变化而变化解释变量，也有翻译成时变解释变量、时变协变量，我觉得也很不错。
大体时变协变量分为几个情况：

  • 内在时依协变量：时依协变量是指随时间变化自变量本身发生变化的那些变量，比如有些患者原来是吸烟的，但在随访过程中戒烟了，这种时依协变量被称为内在时依协变量。
  • 外在时依协变量：还有一种情况，随着时间的变化，模型中自变量本身取值并未发生改变，但其效应却在发生变化，这种时依协变量被称为外在时依协变量。
  • 交互项纳入：有时候我们也会刻意构建一种时依协变量，比如当违背比例风险假定时，我们可以将变量与时间的相乘作为将互项纳入（即使变量本身不一定会随时间变化而变化），这样就可以进行COX回归了。当然我们也可以利用这个原理考察比例风险假定是否满足。

有一些SPSS的教程比较好：
非比例风险的Cox回归模型_分段模型

5.2.2 时依协变量 的特殊数据处理方式

一个典型的例子就是多疗程治疗下用户的死亡时间，如果以用户接受的药剂量来做协变量，则属于一个经典时变变量。
因为用户活得越久，接受大疗程越多，注入的要药剂也越多。换而言之，药剂量在用户的生存期内，是随时间变化的，不像性别这些因素一样保持不变。
这样的问题在用户流失中同样存在，如优惠券的累计发放量，同样与药剂量类似。

对于这种变量，我们需要对原始数据做split。根据变化的时间节点，把原始数据打断为多行。
以用户流失为例，假设某用户在一年内35日、186日、303日分别接受了优惠券：

5.3 参数模型

生存分析简明教程

这些参数模型往往给定了可能的风险函数分布，比如 指数分布、Weibull 和 Gompertz 分布，然后进一步去估计对应的模型参数。
如下图所示，a 为指数分布，其 hazard ratio 为恒定值，在实际中很少应用；b 为 Weibull 分布，可通过不同的参数调整分布的走向；c 为 Gompertz 分布

相对于 Cox 模型，使用这些模型的优点在于分布曲线可根据参数推断，可得到更多信息，
比如：前期死亡率高后期死亡率低，也就是说可以得到更多关于风险分布的信息，而 Cox 模型只能得到有限信息，如风险比及其显著性。

使用这些全参数模型的缺点也是明显的，即固定的分布不一定能满足实际的数据情况，可能带来更多的误差。
再实际使用情况中，可根据不同情况进行选择。

以上是关于生存分析——KM生存曲线hazard比例PH假定检验非比例风险模型（分层/时变/参数模型）的主要内容，如果未能解决你的问题，请参考以下文章

R语言生存分析详解：KM曲线COX比例风险模型HR值解读模型比较残差分析是否比例风险验证：基于survival包lung数据集

生存分析（Survival Analysis）Cox风险比例回归模型（Cox proportional hazards model）及

生存分析（Survival Analysis）Cox风险比例回归模型（Cox proportional hazards model）及

R生存分析 - KM曲线 ，值得拥有姓名和颜值

R|生存分析 - KM曲线 ，值得拥有姓名和颜值

生存曲线（三）：统计分析方法这么多，到底选哪个？