优化算法多策略协同多目标萤火虫算法（MOFA_MOCS）含Matlab源码 1512期

Posted 2021-12-10 紫极神光

一、获取代码方式

获取代码方式1：
完整代码已上传我的资源：【优化算法】多策略协同多目标萤火虫算法（MOFA_MOCS）【含Matlab源码 1512期】

获取代码方式2：
通过紫极神光博客主页开通CSDN会员，凭支付凭证，私信博主，可获得此代码。

获取代码方式3：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

备注：开通CSDN会员，仅只能免费获得1份代码（有效期为开通日起，三天内有效）；
订阅紫极神光博客付费专栏，可免费获得2份代码（有效期为订阅日起，三天内有效）；

二、萤火虫优化算法（FA）简介

1 介绍
萤火虫（firefly）种类繁多，主要分布在热带地区。大多数萤火虫在短时间内产生有节奏的闪光。这种闪光是由于生物发光的一种化学反应，萤火虫的闪光模式因种类而异。萤火虫算法(FA)是基于萤火虫的闪光行为，它是一种用于全局优化问题的智能随机算法，由Yang Xin-She（2009）[1]提出。萤火虫通过下腹的一种化学反应-生物发（bioluminescence）发光。这种生物发光是萤火虫求偶仪式的重要组成部分，也是雄性萤火虫和雌性萤火虫交流的主要媒介，发出光也可用来引诱配偶或猎物，同时这种闪光也有助于保护萤火虫的领地，并警告捕食者远离栖息地。在FA中，认为所有的萤火虫都是雌雄同体的，无论性别如何，它们都互相吸引。该算法的建立基于两个关键的概念：发出的光的强度和两个萤火虫之间产生的吸引力的程度。

2 天然萤火虫的行为
天然萤火虫在寻找猎物、吸引配偶和保护领地时表现出惊人的闪光行为，萤火虫大多生活在热带环境中。一般来说，它们产生冷光，如绿色、黄色或淡红色。萤火虫的吸引力取决于它的光照强度，对于任何一对萤火虫来说，较亮的萤火虫会吸引另一只萤火虫。所以，亮度较低的个体移向较亮的个体，同时光的亮度随着距离的增加而降低。萤火虫的闪光模式可能因物种而异，在一些萤火虫物种中，雌性会利用这种现象猎食其他物种；有些萤火虫在一大群萤火虫中表现出同步闪光的行为来吸引猎物，雌萤火虫从静止的位置观察雄萤火虫发出的闪光，在发现一个感兴趣趣的闪光后，雌性萤火虫会做出反应，发出闪光，求偶仪式就这样开始了。一些雌性萤火虫会产生其他种类萤火虫的闪光模式，来诱捕雄性萤火虫并吃掉它们。

3 萤火虫算法
萤火虫算法模拟了萤火虫的自然现象。真实的萤火虫自然地呈现出一种离散的闪烁模式，而萤火虫算法假设它们总是在发光。为了模拟萤火虫的这种闪烁行为，Yang Xin-She提出了了三条规则（Yang，2009）：
（1）假设所有萤火虫都是雌雄同体的，因此一只萤火虫可能会被其他任何萤火虫吸引。
（2）萤火虫的亮度决定其吸引力的大小，较亮的萤火虫吸引较暗的萤火虫。如果没有萤火虫比被考虑的萤火虫更亮，它就会随机移动。
（3）函数的最优值与萤火虫的亮度成正比。
光强(I)与光源距离（r）服从平方反比定律，因此由于空气的吸收，光的强度(I)随着与光源距离的增加而减小，这种现象将萤火虫的可见性限定在了非常有限的半径内：

萤火虫算法的主要实现步骤如下：

其中I0为距离r=0时的光强（最亮），即自身亮度，与目标函数值有关，目标值越优，亮度越亮；γ为吸收系数，因为荧光会随着距离的增加和传播媒介的吸收逐渐减弱，所以设置光强吸收系数以体现此特性，可设置为常数；r表示两个萤火虫之间的距离。有时也使用单调递减函数，如下式所示。

第二步为种群初始化：

其中t表示代数，xt表示个体的当前位置，β0exp(-γr2)是吸引度，αε是随机项。下一步将会计算萤火虫之间的吸引度：

其中β0表示r=0时的最大吸引度。
下一步，低亮度萤火虫向较亮萤火虫运动：

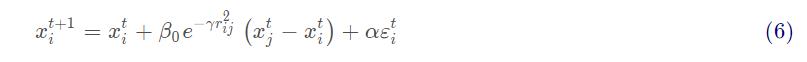
最后一个阶段，更新光照强度，并对所有萤火虫进行排序，以确定当前的最佳解决方案。萤火虫算法的主要步骤如下所示。

Begin
	初始化算法基本参数：设置萤火虫数目n，最大吸引度β0，光强吸收系数γ，步长因子α，最大迭代次数MaxGeneration或搜索精度ε；
	初始化：随机初始化萤火虫的位置，计算萤火虫的目标函数值作为各自最大荧光亮度I0；
	t=1
	while(t<=MaxGeneration || 精度>ε)
		计算群体中萤火虫的相对亮度I(式2)和吸引度β（式5），根据相对亮度决定萤火虫的移动方向；
		更新萤火虫的空间位置，对处在最佳位置的萤火虫进行随机移动（式6）；
		根据更新后萤火虫的位置，重新计算萤火虫的亮度I0；
		t=t+1
	end while
	输出全局极值点和最优个体值。
end

萤火虫算法与粒子群算法(PSO)和细菌觅食算法(BFA)有相似之处。在位置更新方程中，FA和PSO都有两个主要分量：一个是确定性的，另一个是随机性的。在FA中，吸引力由两个组成部分决定：目标函数和距离，而在BFA中，细菌之间的吸引力也有两个组成部分：适应度和距离。萤火虫算法实现时，整个种群(如n)需要两个内循环，特定迭代需要一个外循环(如I)，因此最坏情况下FA的计算复杂度为O(n2I)。

三、部分源代码

function MOFA_MOCS_ZDT1
    %多策略协同多目标萤火虫算法
    %Programmed by Kevin Kong
    %测试问题ZDT-1
    clc;
    global NP N T_MAX gamma beta0 epsilon M V
    NP = 100;%种群大小
    T_MAX = 500;%最大迭代次数
    N = 100;%外部档案规模
    gamma = 1;%光吸收系数
    beta0 = 1;%最大吸引力
    M = 2;%目标函数个数
    V = 30;%决策变量个数
    t = 1;%迭代次数
    epsilon = get_epsilon();
    %变量范围在[0,1]
    min_range = zeros(1,V);
    max_range = ones(1,V);
    pop = init(NP,M,V,min_range,max_range);%初始化种群
    Arc = pop(non_domination_sort(pop,M,V),:);%非支配排序
    while(t <= T_MAX)
        plot(pop(:,V+1),pop(:,V+2),'*');
        str = sprintf('第%d代',t);
        title(str);
        drawnow;
        offspring = pop;%子代
        for i = 1:NP
            for j = 1:NP
                domination = get_domination(pop(i,:),pop(j,:),M,V);
                if(domination ~= -1)
                    %i和j之间存在支配关系
                    g = Arc(1+fix((size(Arc,1)-1)*rand(1)),:);%从Arc里随机选取一个个体作为g*
                    if(domination == 0)
                        %i支配j
                        offspring(j,1:V) = firefly_move(pop(i,:),pop(j,:),V,beta0,gamma,true,g);
                        offspring(j,1:V) = outbound(offspring(j,1:V),V,min_range,max_range);
                    else
                        %j支配i
                        offspring(i,1:V) = firefly_move(pop(j,:),pop(i,:),V,beta0,gamma,true,g);
                        offspring(i,1:V) = outbound(offspring(i,1:V),V,min_range,max_range);
                    end
                else
                    %i和j之间不存在支配关系
                    g = Arc(1+fix((size(Arc,1)-1)*rand(1)),:);%从Arc里随机选取一个个体作为g*
                    res = firefly_move(pop(i,:),pop(j,:),V,beta0,gamma,false,g);
                    offspring(i,1:V) = res(1,:);
                    offspring(i,1:V) = outbound(offspring(i,1:V),V,min_range,max_range);
                    offspring(j,1:V) = res(2,:);
                    offspring(j,1:V) = outbound(offspring(j,1:V),V,min_range,max_range);
                end
            end
        end
        pop = offspring;%更新萤火虫位置
        for i = 1:N
            pop(i,V+1:V+M) = evaluate_objective(pop(i,:));%评估萤火虫个体
        end
        Arc = update_Arc(pop,Arc,N,M,V,epsilon);%利用ε-三点最短路径方法维持Arc档案
        t = t + 1;
    end
end
%% 
function f = init(N,M,V,min,max)
    %初始化种群，随机生成个体并计算其适度值
    %N:种群大小
    %M:目标函数数量
    %V:决策变量数
    %min:变量范围下限
    %max：变量范围上限
    f = [];%存放个体和目标函数值,1:V是决策变量，V+1:V+2是目标函数值
    for j = 1:V
        delta(j) = (max(j) - min(j))/N;%将决策变量x(j)的区间均匀划分成N等分;
        lamda = min(j):delta(j):max(j);%得到N个子区间
        for i = 1:N
            %从N个子区间中随机选择一个
            [~,n] = size(lamda);%获得子区间个数n
            rand_n = 1 + fix((n-2)*rand(1));%随机位置
            min_range = lamda(rand_n);%获得子区间的下限
            max_range = lamda(rand_n+1);%获得子区间的上限
            f(i,j) = min_range + (max_range - min_range)*rand(1);%随机生成
            lamda(rand_n) = [];%删除该子区间
        end
    end
    %计算个体的适度值
    for i = 1:N
        f(i,V+1:V+M) = evaluate_objective(f(i,:));%计算目标函数值
    end
end
%%
function f = evaluate_objective(x)
    %根据目标函数计算适度值，测试方法：ZDT-1
    global V 
    f = [];
    f(1) = x(1);%目标函数1
    g = 1;
    g_tmp = 0;
    for i = 2:V
        g_tmp = g_tmp + x(i);
    end
    g = g + 9*g_tmp/(V-1);
    f(2) = g*(1-sqrt(x(1)/g));%目标函数2
end
%%
function f = non_domination_sort(x,M,V)
    %非支配排序,得到非支配解集
    %M:目标函数数量
    %V:决策变量数
    [N,~] = size(x);%获取种群个体数
    rank = 1;%pareto等级
    F(rank).f = [];%非支配解集
    pop = [];%种群
    for i = 1:N
        %得到最高等级个体和个体间的支配关系
        pop(i).np = 0;%被支配数
        pop(i).sp = [];%支配个体集合
        for j = 1:N
            %个体支配规则：对任意的目标函数，均有fk(x1)<=fk(x2)，且存在fk(x1)<fk(x2)
            domination = get_domination(x(i,:),x(j,:),V,M);%获得i和j之间的支配关系
            if(domination == 0)
                %i支配j
                pop(i).sp = [pop(i).sp j];%把个体j的索引加入支配集合中
            elseif(domination == 1)
                %i被j支配
                pop(i).np = pop(i).np + 1;%i的被支配数+1
            end
        end
        if(pop(i).np == 0)
            x(i,V+3) = rank;%rank等级最高，为1
            F(rank).f = [F(rank).f i];%把个体i加入到非支配解集中
        end
    end
    f = F(rank).f;
end
%%
function res = get_domination(x1,x2,V,M)
    %获得两个个体的支配关系，x1支配x2返回0，x2支配x1返回1，否则返回-1
    less = 0;%小于
    equal = 0;%等于
    more = 0;%大于
    for k = 1:M
        %遍历每一个目标函数
        if(x1(V+k) < x2(V+k))
            less = less + 1;
        elseif(x1(V+k) == x2(V+k))
            equal = equal + 1;
        else
            more = more + 1;
        end
    end

四、运行结果

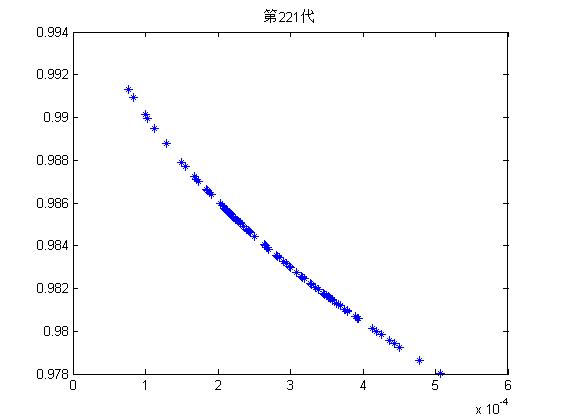
五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]群体智能优化算法之萤火虫算法(Firefly Algorithm，FA)