优先级队列总结

Posted 2021-12-10 ohana！

目录

一，堆的应用

1.PriorityQueue的实现

2.利用堆的思想来进行堆排序

3.代码实现步骤

二， Top k 问题

---

一，堆的应用

1.PriorityQueue的实现

优先级队列的底层就是用堆实现的

2.利用堆的思想来进行堆排序

• 建堆

1. 升序：建大堆
2. 降序：建小堆

• 利用堆删除的思想来进行排序

1. 堆删除的实现------将堆的根节点和最后一个节点进行交换，并将堆的有效元素的个数减“1“”，并对新的堆进行向下调整
2. 排序的思想：将已经完成向下调整的根节点与最后一个结点交换位置，此时，新的堆一定不满足要求，重新进行向下调整，每次调整前将堆中的有效元素进行减“1“”的操作，直到结束 

3.代码实现步骤

1.实现向下调整的方法

    //   向下调整的方法
    private static void shiftDown(int[] array,int size,int parent) {
        int child = parent * 2 + 1;

        //标记左右孩子
        while (child < size) {
            if ((child + 1 < size) && (array[child + 1] > array[child])) {
                child = child + 1;
            }

            if (array[parent] < array[child]) {
                int temp = array[parent];
                array[parent] = array[child];
                array[child] = temp;

                parent = child;
                child = parent * 2 + 1;
            }else{
                return;
            }
        }
    }

2.实现堆排序的方法

    //实现堆排序的方法
    public static void heapSort(int[] array) {
        for (int root = ((array.length - 2) >> 1); root >= 0; root--) {
            shiftDown(array,array.length,root);
        }
        int end = array.length - 1;
        while (end >= 0) {
            int temp = array[0];
            array[0] = array[end];
            array[end] = temp;
            shiftDown(array,end,0);
            end--;
        }
    }

3.传入测试用例进行测试

    public static void main(String[] args) {
        //  目标 ： 实现升序（由小到大）----->  建大堆
        int[] array = {5,15,10,8,1,6,20,19,27,30};
        heapSort(array);
    }
}

最终是否排序成功，通过监视窗口可以观察到

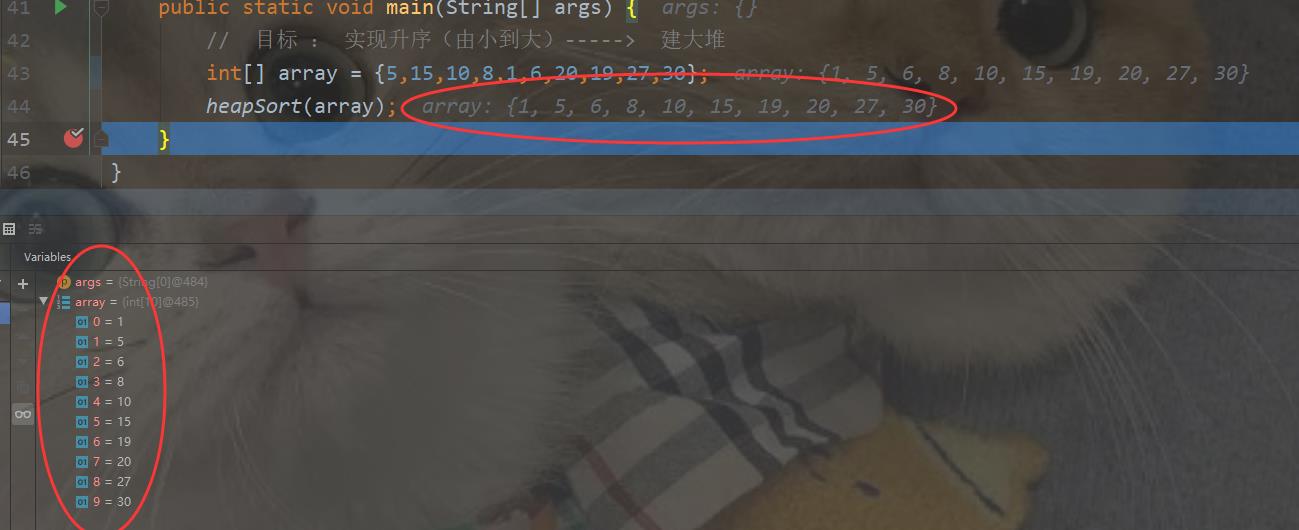
4.堆排序完整代码

public class TestPriorityQueue {
    //   向下调整的方法
    private static void shiftDown(int[] array,int size,int parent) {
        int child = parent * 2 + 1;

        //标记左右孩子
        while (child < size) {
            if ((child + 1 < size) && (array[child + 1] > array[child])) {
                child = child + 1;
            }

            if (array[parent] < array[child]) {
                int temp = array[parent];
                array[parent] = array[child];
                array[child] = temp;

                parent = child;
                child = parent * 2 + 1;
            }else{
                return;
            }
        }
    }

    //实现堆排序的方法
    public static void heapSort(int[] array) {
        for (int root = ((array.length - 2) >> 1); root >= 0; root--) {
            shiftDown(array,array.length,root);
        }
        int end = array.length - 1;
        while (end >= 0) {
            int temp = array[0];
            array[0] = array[end];
            array[end] = temp;
            shiftDown(array,end,0);
            end--;
        }
    }
    public static void main(String[] args) {
        //  目标 ： 实现升序（由小到大）----->  建大堆
        int[] array = {5,15,10,8,1,6,20,19,27,30};
        heapSort(array);
    }
}

5.堆排序的时间复杂度

建堆的时间复杂度为O(n),调整堆的时间复杂度为O(n logn),总的时间复杂度为O(nlogn） 

二， Top k 问题

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大

 解决思路：

• 用前k个元素建堆

1. 前k个最大的元素，则建小堆
2. 前k个最小的元素，则建大堆

• 利用建好的堆，将剩余的元素与这个堆顶的元素进行比较，最后留下的就是需要的前k各元素